Булевы операции над объемами понятий.

Операции над понятиями, точнее – над объемами понятий, то есть классами называются булевыми, по имени английского логика Дж. Буля, построившего особую алгебру логики, получившую в его честь название булевой алгебры.

Предположим, что даны два понятия aА(a)иaВ(a). Условимся, что род у этих понятий один и тот же. Объемы этих понятий будем сокращенно обозначать просто буквами А и В (читается: «класс А» и «класс В»). Тогда с этими объемами можно осуществить следующие операции:

а) пересечение (АÇВ) б) объединение (АÈВ)

В

в) вычитание (А\В) г) взятие дополнения (ØА)

Штриховкой на схемах обозначен результат применения соответствующих операций к классам А и В.

Пересечение объемов двух понятий равняется классу предметов, которые входят одновременно в объем каждого из них. Объединение двух понятий равняется классу предметов, которые входят в объем по крайней мере одного из них. Вычитание объема одного понятия из объема другого равняется классу предметов, которые входят в объем первого понятия, но не входят в объем второго. Дополнение к объему понятия представляет собой класс предметов, которые не входят в объем этого понятия.

26. Основные законы булевой алгебры, их характеристика.

Между понятиями существуют объективные, независящие от человека отношения. Прежде всего, это отношения сравнимости и несравнимости.

Два понятияaА(a)иaВ(a)являютсясравнимыми,если и только если их универсумы совпадают. Например, понятия о преступнике и о жертве преступления являются сравнимыми. Оба они относятся к одной и той же предметной области – универсуму людей.

Два понятияaА(a)иaВ(a)являютсянесравнимыми,если они относятся к различным универсумам. Например, понятие о четном числе и понятие о европейской столице являются несравнимыми, поскольку первое из них имеет своим родом универсум чисел, а второе – универсум городов.

Среди всевозможных пар сравнимых понятий можно выделить три фундаментальных отношения в том смысле, что с их помощью возможно задать все остальные отношения. К числу фундаментальных принадлежат отношения совместимости, включения и исчерпывания.

Фундаментальные отношения:

1) ПонятияaА(a) и aВ(a) находятся в отношении совместимости, если и только если пересечение их объемов А и В не пусто, то есть АÇВ ¹ Æ.Это означает, что в универсуме имеется по крайней мере один элемент, обладающий как признаком А(a), так и признаком В(a) (например, А – студент, В – спортсмен).

2) Понятие aВ(a) находится к понятию aА(a) в отношении включения если и только если при вычитании объема aА(a)из объемаaВ(a)получается пустое множество, то есть В\A = Æ.Это означает, что всякий элемент универсума, обладающий признаком В(a), обладает также признаком А(a)(например, А – учащийся, В– студент).

3) Понятия aА(a) и aВ(a) находятся в отношении исчерпывания, если и только если объединение их объемов А и В равно универсуму, то есть АÈВ = U.Это означает, что каждый элемент универсума обладает признаком А(a) или признаком В(a)(например, А – сын, В – дочь; каждый человек является чьим-то сыном или дочерью).

Вспомогательные отношения выводятся из фундаментальных. Наиболее важными из них являются: равнообъемность, подчинение, соподчинение, противоречие, дополнение, перекрещивание.

(1)А и В равнообъемны (2) А подчиняется В (3) А и В соподчиняются

прямоуг. с равными сторонами большой город,большой европ.город европ город,австралийский город

ромб с прямыми углами (несовместимы,не исчерпывают)

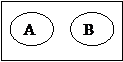
А,в

(4) А противоречит В(5) А дополняет В(6) А и В перекрещиваются

летат. аппарат легче/тяжелее воздуха рос.город,расплож. западнее байкала/ студент 1 курса,студ-т изуч. логику

(несовместимы,исчерпывают) восточнее урала (совместимы,исчерпывают) (совместимы,не исчерпывают)

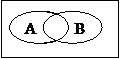А В А В

27.Логические отношения между сложными суждениями.

В процессе построения отношений между суждениями можно выделить сравнимые и несравнимые. Сравнимые суждения имеют общий субъект и предикат. Несравнимые суждения не имеют общего субъекта и предиката. Они делятся на: совместимые и несовместимые.

Несовместимыми называются суждения, у которых из истинности одного из них необходимо следует ложность другого, то есть эти суждения не могут оказаться одновременно истинными. Например, числа 1,2,3,4,… являются несовместимыми.

Совместимые суждения выражают одно и то же высказывание полностью или частично, поэтому могут быть одновременно истинными. К ним относятся отношения: эквивалентности, подчинения и субконтрарности (частичного совпадения).

Эквивалентность означает, что суждения совместимы по истинности, совместимы по ложности и из первого следует второе и наоборот.

Подчинение означает, что суждения совместимы по истинности, совместимы по ложности, из первого следует второе, но не наоборот.

Субконтрарность означает,что суждения совместимы по истинности, но не совместимы по ложности и логического следования нет.

Между логическими суждениями, высказываниями (с одинаковыми терминами) можно установить четыре типа отношений. В период Средневековья логики наглядно изображали их с помощью так называемого «логического квадрата»:

Aконтрарность Е

п е

п р и п

о о ч о

д т е д

ч и р ч

и в о и

н в о н

е и р е

н т е н

и о ч и

е р и е

п е

IсубконтрарностьО

Рассмотрим эти отношения между суждениями с помощью логического квадрата. В отношении подчинения находятся суждения форм A и I, а также суждения E и O. Например, общеутвердительное суждение «Все студенты первого курса изучают историю» является подчиняющим, а частноутвердительное суждение «Некоторые студенты первого курса изучают историю» является подчиненным.

Отношения субконтрарности (частичное совпадение)) имеет место между суждениями форм I и O, если они имеют одинаковые субъекты и одинаковые предикаты. Они являются совместимыми по истинности, но несовместимыми по ложности. Например, частноутвердительное суждение «Некоторые студенты-первокурсники занимаются в научных кружках» и частноотрицательное суждение «Некоторые студенты-первокурсники не занимаются в научных кружках». Оба суждения могут быть одновременно истинными, но ложными одновременно не могут быть.

Отношения несовместимости имеют место между отношениями контрарности (противоположность) и контрадикторности (противоречие). При этом контрарностьпоказывает отношения между суждениями форм A и E, которые совместимы по ложности, но не совместимы по истинности. Например, не могут быть одновременно истинными два суждения: «Все студенты учебной группы изучают китайский язык» и «Ни один студент учебной группы не изучает китайский язык».

Отношения котрадикторности имеют место между суждениями A и O, а также E и I. Они не совместимы по истинности и по ложности. Например, общеутвердительное суждение «Все люди обладают сознанием» и частноотрицательное суждение «Некоторые люди не обладают сознанием». Эти суждения не могут быть одновременно истинными и ложными. Также пример для общеотрицательного суждения «Ни один студент не может быть профессором» и частноутвердительного суждения «Некоторые студенты являются профессорами».