Состав и виды атрибутивных суждений. Язык и семантика силлогистики.

Силлогистика является исторически первой дедуктивной теорией, ее отец – Аристотель. Благодаря своей простоте и естественности она выступала образцом и основой логической науки на протяжении двух тысячелетий.

Силлогистика – это теория, изучающая логическую структуру простых атрибутивных высказываний, отношения между ними и выводы, построенные с учетом этой структуры. (С современной точки зрения, как будет показано ниже, это в сущности логика непустых и неуниверсальных одноместных предикатов).

Простыми называются высказывания, не содержащие внутри себя пропозициональных связок.

Атрибутивными (от лат. "atribut" – свойство) называются высказывания о наличии или отсутствии некоторого свойства у определенного класса предметов.

Например, "Некоторые художники талантливы", "Ни один бегемот не летает" и т.п. В составе атрибутивных высказываний выделяют четыре структурных элемента:

1. Субъект (логическое подлежащее) – термин, обозначающий те предметы, о которых в высказывании нечто утверждается или отрицается.

2. Предикат (логическое сказуемое) – термин, обозначающий свойство, наличие которого утверждается или отрицается у этих предметов.

3. Кванторное (количественное) слово – указывает, о каком количестве предметов идет речь. Слова "все", "каждый", "ни один" выражают всеобщность приписываемого свойства относительно данного класса предметов. Слова "некоторые", "по крайне мере один", "существует" выражают существование в данном классе предметов с указанным свойством.

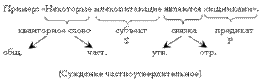4. Связка – слово, которое утверждает или отрицает наличие некоторого свойства у субъекта. Связки делятся на утвердительные ("есть, "является", "суть") и отрицательные ("не есть", "не является", "не суть").

Исходя из их логической структуры, атрибутивные высказывания принято делить по качеству – на утвердительные и отрицательные, и по количеству – на общие и частные.

Язык силлогистики предназначен для того, чтобы выражать состав, структуру и вид атрибутивных высказываний. Его алфавит включает в себя:

Переменные для терминов – S, P, М, …

Силлогистические константы – a, e, i, o.

Символ внутреннего ( терминного ) отрицания – ~.

Символ внешнего (пропозиционального) отрицания – .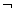

Скобки – ( , ).

Осмысленными выражениями в силлогистике являются термы и формулы.

Определение терма. (1) Терминные переменные являются термами; (2) Если Х терм, то ~X тоже терм; (3) Ничто другое не является термом.

Определение формулы. (1) Если Х и Y – термы, то XaY, XeY, XiY и XoY – формулы; (2) Если А формула, то 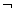А также являются формулой; (3) Ничто другое не является формулой.

Терминные переменные относятся к нелогическим параметрам – они передают содержание атрибутивных высказываний (буквой S обычно принято обозначать субъект, буквой Р – предикат).

Терминное отрицание "~" служит для того, чтобы изменять смысл термина на противоположный: если S означает "воспитанный", то ~S – "невоспитанный", и т.д. В естественном языке внутреннему отрицанию обычно соответствуют отрицательные приставки ("не-", "без-", "дис-", "а-" и т.п.).

Силлогистические константы выражают собой тип высказывания:высказывания:

высказывания	общие	частные
утвердительные	a	i
отрицательные	e	o

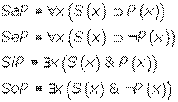– эти гласные буквы были взяты средневековыми логиками из латинских слов "affirmo" (утверждаю) и "nego" (отрицаю). Соединение терминов с помощью констант дает четыре элементарных силлогистических формулы:

SaP : Все S есть Р.
SeP : Ни один S не есть Р.
SiP : Некоторые S есть Р.
SoP : Некоторые S не есть Р.

Перевод силлогистических формул на язык КЛП:

Внешнее отрицание " 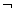" используется для того, чтобы отрицать всю формулу в целом. Ни в коем случае нельзя путать внешнее и внутреннее отрицание. В результате применения " 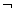" и "~" мы получаем два различных высказывания. Сравните:

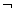SaP	Неверно, что ( 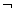)все дети (S)являются воспитанными (Р).
Sa~P	Все дети (S)являются невоспитанными (~P).

Семантика силлогистики проста. Она задается на круговых схемах (т.н. "кругах Эйлера"). Каждому термину сопоставляется определенный класс предметов, графически обозначаемый с помощью круга. Например, термину "хищники" соответствует выделенный среди множества животных класс хищников:

Термину с отрицанием ~Sсоответствует класс предметов, не входящих в S:

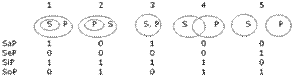Каждое атрибутивное высказывание будем рассматривать как утверждение о полном или частичном включении (невключении) одного класса в другой. Используя круговые схемы, условия истинности формул SaP, SeP, SiP и SoP можно задать следующим образом.

Множество предметов класса S, относительно которых справедливо данное атрибутивное суждение, называется объемом сказывания. Объем сказывания на круговых схемах обозначается штриховкой.

Суждение SaP истинно на схемах	Суждение SoP истинно на схемах
Суждение SeP истинно на схемах	Суждение SiP истинно на схемах

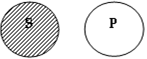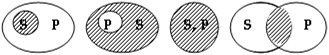С помощью круговых схем вводится также очень важное семантическое понятие распределенности терминов. Термин в атрибутивном высказывании считается распределенным, если и только если на всех модельных схемах, где это высказывание истинно, его объем полностью заштрихован или полностью незаштрихован.

Условимся помечать распределенные термины знаком "+", а нераспределенные – знаком "–". В предложении "Все квадраты являются прямоугольниками" субъект ("квадраты") распределен, а предикат ("прямоугольники") нераспределен. Символически: S⁺aP^–.

Нетрудно видеть, что субъекты распределены только в общих суждениях, а предикаты – только в отрицательных. Иначе говоря.