Отношения между простыми категорическими суждениями. «Логический квадрат».
Простые категорические суждения делятся на сравнимые и несравнимые.
Несравнимыми являются суждения, имеющие разные субъекты или предикаты. Таковы, например, два суждения: «Некоторые студенты первокурсники» и «Некоторые студенты заочники».
Сравнимыми являются суждения с одинаковыми субъектами и предикатами и различающиеся связкой или квантором.
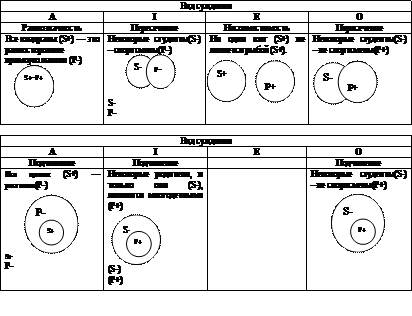
Эти отношения обычно рассматриваются с помощью схемы, называемой логическим квадратом. Его вершины символизируют простые категорические суждения — А, Е, I, О; стороны и диагонали — отношения между суждениями.
Для систематизации этих отношений был придуман так называемый “логический квадрат”, который выглядит следующим образом:
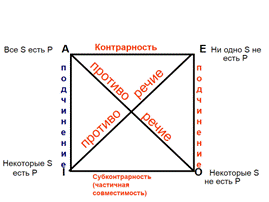
Между двумя сравнимыми суждениями возможны следующие отношения:
- подчинение;
- противоположность (контрарность);
- Субконтрарность (частичная совместимость);
- противоречие (контрадикторность).
Подчинение – это отношение, при котором истинность подчиняющего суждения гарантирует истинность подчинённого.
Так, если суждение “Все планеты солнечной системы вращаются вокруг солнца.” — истинно, то суждение “Некоторые планеты солнечной системы вращаются вокруг солнца.” будет также истинным
  А А  Е Е | I О |
| И | И |
| И | Л |
| Л | И |
| Л | Л |
Противоположность (контрарность) – это отношение, при котором два суждения не могут быть оба истинными, но могут быть оба ложными.
Отношение противоположности (контрарности) имеет место между общеутвердительными суждениями (А) и общеотрицательными (Е).

| А | Е |
| И | И |
| И | Л |
| Л | И |
| Л | Л |
Частичная совместимость (субконтрарность) – это отношение, при котором два суждения не могут быть оба ложными, но могут быть оба истинными.
Отношение субконтрарности имеет место между частноутвердительными суждениями (I) и частноотрицательными (О).
Так суждения “Некоторые правонарушения являются преступлениями.” и ”Некоторые правонарушения не являются преступлениями.” не могут быть вместе ложными, но могут быть вместе истинными (каковыми и являются).

| I | О |
| И | И |
| И | Л |
| Л | И |
| Л | Л |
Противоречие – это отношение, при котором два суждения не могут быть оба ни истинными, ни ложными (то есть одно из них всегда истинно, другое всегда ложно).
Отношение противоречия имеет место между общеутвердительными суждения (А) и частноотрицательными (О), а также между общеотрицательными (Е) и частноутвердительными (I ).
Так два суждения: “Все преступления наказуемы.” и ”Некоторые преступления не наказуемы.” не могут быть одновременно ни истинными, ни ложными.

| А I | О Е |
| И | И |
| И | Л |
| Л | И |
| Л | Л |
Распределенность терминов в суждениях
В логических операциях с суждениями возникает необходимость установить, распределены или не распределены его термины — субъект и предикат.
Если субъект или предикат в суждении мыслится во всем объеме, он считается распределенным, если же термин мыслится только частично — нераспределенным.
Субъект всегда распределён только в общих суждениях, а предикат — только в отрицательных.
Если распределённый термин обозначать знаком “+”, а нераспределённый — знаком “--”, то распределённость терминов в простых категорических суждениях можно выразить следующим образом:
Все S+ есть Р― ;
Ни одно S+ не есть Р+;
Некоторые S― есть Р― ;
Некоторые S― не есть Р+.
Распределенность терминов
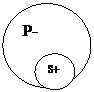
1. В общеутвердительном суждении (А): «Все S есть Р» встречаются два случая:
а) субъект распределен, а предикат не распределен; Все цветы – растения. S+, P - Все адвокаты― юристы.
б) субъект и предикат взаимно распределены. Все квадраты― равносторонние рямоугольники
 |  | ||
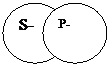
2. В частноутвердительном суждении (I): «Некоторые S есть Р» встречаются два случая:
а) субъект и предикат не распределены; Некоторые студенты(S-) – спортсмены(Р-).«
б) субъект не распределен, а предикат распределен. Некоторые родители, и только они (S-), являются многодетными (Р+)».
 | |||
 | |||
 P
P
3. В общеотрицательном суждении (Е): «Ни одно S не есть Р» всегда субъект и предикат распределены. «Ни один студент нашей группы (S+) не является неуспевающим (Р-)».
 |  | ||
PР+
4. В частноотрицательных суждениях (О): «Некоторые S не есть Р» возможны два случая, но в обоих случаях субъект не распределен, а предикат распределен.
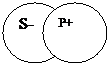 | 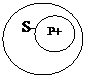 | ||
Некоторые птицы не являются водоплавающими. «Некоторые студенты нашей группы (S-) — не отличники (Р+)».
| Виды суждения Термины | A | I | E | О |
| S | + | - | + | - |
| Р | - | - | + | + |
| Р выделяющих суждений | + | + | + | + |
Сложные суждения
Сложным называется суждение, состоящее из нескольких простых, соединенных логическими связками.
Различают следующие виды сложных суждений:
1) соединительные,
2) разделительные,
3) условные,
4) эквивалентные.
Истинность таких суждений определяется истинностью составляющих их простых.
Соединительные суждения
1. Соединительным, или конъюнктивным, называется суждение, состоящее из нескольких простых, соединенных логической связкой «и».
Например, суждение «Кража и мошенничество относятся к умышленным преступлениям» является соединительным суждением, состоящим из двух простых:
«Кража относится к умышленным преступлениям»,
«Мошенничество относится к умышленным преступлениям».
Если первое обозначать р, а второе — q, то соединительное суждение символически можно выразить как р Λ q, где р и q — члены конъюнкции (или конъюнкты), Λ — символ конъюнкции.
В естественном языке конъюнктивная связка может быть представлена и такими союзами (логическими связками): «тоже», «но», «а также», «как и», «хотя», «однако», «несмотря на» и другими.
Соединительное суждение может быть как двух-, так и многосоставным
В языке соединительное суждение может быть выражено одной из трех логико-грамматических структур.
- В форме простого суждения со сложными субъектами: S1 и S2 есть Р. Например: «Конфискация имущества и лишение звания являются дополнительными уголовно-правовыми санкциями».
- В форме простого суждения со сложным предикатом: S есть P1 и Р2. Например: «Преступление — это общественно опасное и противоправное деяние».
- В форме простого суждения со сложным субъектом и сложным предикатом: S1 и S2 есть Р1 и Р2.
- Например: «С полицмейстером и прокурором Ноздрев тоже был на «ты» и обращался по-дружески» (Н. В. Гоголь).
Таблица истинности конъюнктивного суждения
| p | q | p 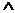 q q |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
Соединительное суждение истинно при истинности всех составляющих его конъюнктов и ложно при ложности хотя бы одного из них. Условия истинности суждения р 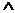 q показаны в таблице, где истинность обозначена И, а ложность Л. В первых двух столбцах таблицы р и q берутся как независимые и принимают поэтому все возможные сочетания значений И и Л: ИИ, ИЛ, ЛИ, ЛЛ. В третьем столбце показано значение суждение р
q показаны в таблице, где истинность обозначена И, а ложность Л. В первых двух столбцах таблицы р и q берутся как независимые и принимают поэтому все возможные сочетания значений И и Л: ИИ, ИЛ, ЛИ, ЛЛ. В третьем столбце показано значение суждение р 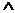 q. Из четырех построчных вариантов истинным оно является лишь в 1-й строке, когда истинны оба конъюнкта: и р, и q. Во всех остальных случаях оно ложно: во 2-й и 3-й строках в силу ложности одного из членов, а в 4-й в силу ложности обоих членов.
q. Из четырех построчных вариантов истинным оно является лишь в 1-й строке, когда истинны оба конъюнкта: и р, и q. Во всех остальных случаях оно ложно: во 2-й и 3-й строках в силу ложности одного из членов, а в 4-й в силу ложности обоих членов.
