Особенности минимизации неполностью определенных логических функций
При решении практических задач синтеза дискретных устройств широко
используются неполностью определенные логические функции. Так как неполностью определенной логической функции соответствует совокупность полностью определенных функций, то их тупиковые и минимальные нормальные формы могут существенно отличаться друг от друга по количеству букв. Особенностью минимизации неполностью определенной функции является то, что необходимо найти такое ее доопределение на условных наборах, которое соответствует минимальной нормальной форме, содержащей наименьшее число букв. Другими словами, при решении задачи минимизации неполностью определенной функции, условные наборы должны быть использованы для получения наиболее простой записи функции в заданной функционально полной системе элементарных логических функций.
Пусть 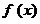 - неполностью определенная функция, имеющая k определенных наборов. Тогда путем доопределения значений неполностью определенной функции на неопределенных наборах можно получить
- неполностью определенная функция, имеющая k определенных наборов. Тогда путем доопределения значений неполностью определенной функции на неопределенных наборах можно получить 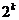 полностью определенных функций, единичные и нулевые наборы которых совпадают. Выделим из этого множества две функции
полностью определенных функций, единичные и нулевые наборы которых совпадают. Выделим из этого множества две функции 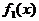 и
и  , которые получаются из функции
, которые получаются из функции 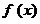 путем ее доопределения на всех неопределенных наборах соответственно значениям только 1 или 0.
путем ее доопределения на всех неопределенных наборах соответственно значениям только 1 или 0.
Применительно к решению задачи минимизации неполностью определенных логических функций обобщим некоторые введенные ранее определения.
Простой импликантой неполностью определенной функции 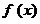 будем называть всякую простую импликанту функции
будем называть всякую простую импликанту функции 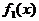 .
.
Простой имплицентой неполностью определенной функции 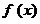 будем называть всякую простую имплиценту функции
будем называть всякую простую имплиценту функции  .
.
Простую импликанту (имплиценту) неполностью определенной функции 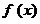 будем называть существенной, если она накрывает хотя бы один единичный (нулевой) набор этой функции. Например, неполностью определенная функция
будем называть существенной, если она накрывает хотя бы один единичный (нулевой) набор этой функции. Например, неполностью определенная функция 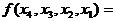 [1, 2, 3, 6, 7, 10, 12 (11, 13, 16, 17)]
[1, 2, 3, 6, 7, 10, 12 (11, 13, 16, 17)]  содержит условные наборы {0, 4, 5, 14, 15}
содержит условные наборы {0, 4, 5, 14, 15}  . Тогда
. Тогда 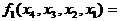 [0, 1, 2, 3, 4, 5, 6, 7, 10, 12, 14, 15 (11, 13, 16, 17)]
[0, 1, 2, 3, 4, 5, 6, 7, 10, 12, 14, 15 (11, 13, 16, 17)]  , а
, а 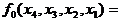 [1, 2, 3, 6, 7, 10, 12, (0, 4, 5, 11, 13, 14, 15, 16, 17)]
[1, 2, 3, 6, 7, 10, 12, (0, 4, 5, 11, 13, 14, 15, 16, 17)]  .
.
Для функции 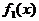 простыми имликантами являются
простыми имликантами являются
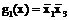 ;
;
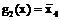 ;
;
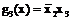 .
.
Эти же конъюнкции являются простыми импликантами функции 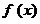 , однако импликанта
, однако импликанта 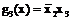 является несущественной, так как накрывает только неопределенные наборы 4, 5, 14, 15 функции
является несущественной, так как накрывает только неопределенные наборы 4, 5, 14, 15 функции 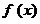 .
.
Для функции  простыми имплицентами являются
простыми имплицентами являются
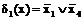 ;
; 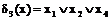 ;
;
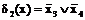 ;
; 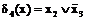 .
.
Эти же дизъюнкции являются простыми имплицентами функции 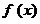 , однако имплиценты
, однако имплиценты 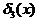 и
и 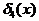 являются несущественными, так как накрывают только неопределенные наборы функции
являются несущественными, так как накрывают только неопределенные наборы функции 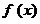 .
.
Дизъюнкция (конъюнкция) всех существенных простых импликант (имплицент) неполностью определенной логической функции называется сокращенной ДНФ (КНФ) этой функции.
Тупиковой ДНФ (КНФ) неполностью определенной логической функции 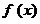 называется дизъюнкция (конъюнкция) приведенной системы существенных простых импликант (имплицент).
называется дизъюнкция (конъюнкция) приведенной системы существенных простых импликант (имплицент).
Очевидно, что для полностью определенной логической функции 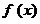 выполняется равенство
выполняется равенство
 =
= 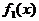 =
= 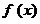 .
.
Полностью определенную функцию можно рассматривать как частный случай неполностью определенной логической функции, у которой число неопределенных наборов равно нулю. В связи с этим методы минимизации неполностью определенных функций логических функций могут быть легко распространены на полностью определенные функции.
