Iii. сонеты и числа, птицы и здания
Сонет совершенен.
Структурную гармониюστέφανοσ можно соотносить с морфологией и кристаллов, и организмов. Системные инварианты разнообразны! Все они поддаются математической формализации. Перефразируя Пифагора, скажем так: числа правят сонетом.
В 1223 г. Фридрих II Гогенштауфен проезжал через Пизу. Там он познакомился с Леонардо Пизанским – он же Фибоначчи (ок. 1170 – ок. 1250). Общение продолжилось в Палермо. Двор сицилийского короля в те годы – по концентрации ярких умов – далеко превосходил и Оксфорд, и Сорбонну. Уникальная творческая атмосфера благоприятствовала озарениям.
Диалог эвристичен.
В Палермо процвёл полиалог. Сегодня мы назвали бы его междисциплинарным – в нём участвовали и гуманитарии, и естественники, и математики.
Хотя тут возможно некоторое рассогласование во времени, но в принципе легко представить, как Леонардо Пизанский беседует с Якопо Лентини. Их интересы конвергируют в στέφανοσ. Там мы найдём и числа Фибоначчи, и золотое сечение – это разное выражение одной закономерности. Конечно же, подобная проблематика тогда не могла возникнуть – но потенциально она уже наметилась: её осознание происходит сегодня.
В 1202 г. Леонардо Пизанский написал «Книгу абака». В ней мы находим знаменитую рекуррентную последовательность:
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
21 + 34 = 55
34 + 55 = 89
и т.д...
Хороший пример рекурренции – взаимоотражения в двух зеркалах.
Игра идёт на самоповторе – самоподобии – самовозврашении. В пространствеστέφανοσ эта игра идёт по более сложным правилам. Однако исходный алгоритм одинаковый.
Венок сонетов растёт как живая система.
Рекурренция – закон этого роста.
Бесконечного – в потенциале – роста!
Сонет рекуррентно вырастает в венок, венок – в корону, корона – в корону корон и т.д. Захватывающая перспектива!
Венок цикличен, периодичен.
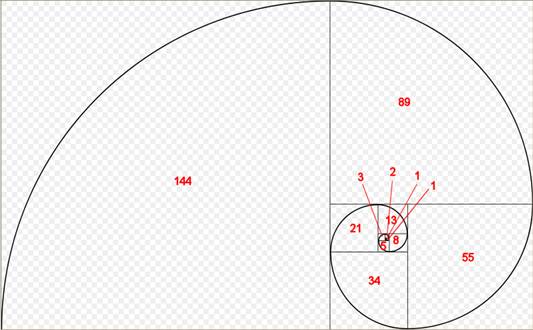
Спиральная сущность венка сонетов
Однако его самовозобновление не ведёт к тавтологии.
Венок возвращается к себе – инверсируется. Но это инверсия иного рода, нежели та, которую мы видим в ракоходной фуге или палиндроме. Зеркальность там буквальная, механическая – тогда как в στέφανοσ она предполагает увеличение, умножение: наличествует поступательная прогрессия.
Вот зеркально-симметричная запись чисел Фибоначчи: ряд уходит и влево, и вправо – в (–) пространство и (+) пространство:
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | |||||||||||
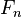 | −55 | −21 | −8 | −3 | −1 |
В структуре στέφανοσ при желаниине трудно отыскать что-то похожее на пассивно-отражательную плоскость. Велика ли её роль? Она кажется незначительной в сравнении со способностью венка рекуррентно укрупнять масштабы – наращивать обороты.
Как если бы отражение осуществлялось в гиперболическом зеркале! Поэтому вместо per motum retrogradum – попятного движения – мы видим восходящую траекторию, где повторы предполагают постоянное обновление смысла, мелодики, интонации.
Этот процесс находит своё адекватное воплощение – и гносеологически точное, и художественно выразительное – в упоительном развороте логарифмической спирали.
Вот икона στέφανοσ!
Вот его душа!
Числа Фибоначчи управляют экспансией прекрасных витков.
Леонардо Пизанский много путешествовал по странам Востока. Он вчитывался в труды не только арабских, но и индийских математиков – именно им принадлежит честь открытия рекуррентной последовательности, которая носит его имя.
