Проверка правильности формы умозаключения на диаграммах Эйлера – Венна
Наконец мы подошли к самому важному и полезному пункту нашего изложения.
Определение 17.1.Умозаключение (рассуждение) – это логическое действие, позволяющее получать новое знание из уже имеющегося.
Фактически, умозаключение представляет собой импликацию вида
А1⋀ А2⋀ … ⋀Аn →В, (17.1)
где А1, А2, … ,Аn - связанные между собой по смыслу высказывания, называемые посылками, а В – высказывание, называемое выводом.
Определение 17.2.Говорят, что умозаключение обладает правильной формой , если при любых предположениях об объемах понятий, используемых в посылках, из истинности посылок следует истинность вывода.
Пример1(иллюстрация к закону контрапозиции для предикатов).
Если лягушка квакает, то она довольна собой
Если лягушка недовольна собой, то она не квакает (17.2)
В этом примере у нас имеется одна-единственная посылка: «Если лягушка квакает, то она довольна собой».
“На языке предикатов и кванторов” умозаключение (17.2) запишется в виде
[ 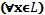 K(x) →Д(x)] →[
K(x) →Д(x)] →[ 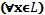 ⅂Д(x) →⅂K(x)] . (17.2’)
⅂Д(x) →⅂K(x)] . (17.2’)
Здесь L – множество лягушек, K(x) – «лягушка х квакает», Д(x) – «лягушка х довольна собой». Истинность посылки, очевидно, означает, что для множеств истинности предикатов K(x) и Д(x) должно быть выполнено включение
Kи 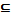 Ди
Ди
(см. по этому поводу также п.7). Однако из этого включения немедленно следует “обратное” включение для дополнений к соответствующим множествам истинности:
(Ди)’ 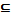 (Kи)’ ,
(Kи)’ ,
откуда, в свою очередь, следует истинность вывода в (17.2) (см. рис. 17.1).
Замечание.Умозаключение (17.2), очевидно, можно было бы переписать также “на языке множеств”:
Kи 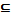 Ди (17.2”)
Ди (17.2”)
(Ди)’ 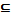 (Kи)’
(Kи)’
Пример 2.
Некоторые розы – красные
Ни одна собака не красная
Ни один фокстерьер не красный (17.3)
Фокстерьеры – это собаки
Мы предоставляем читателю возможность переписать (17.3) «на языке предикатов и кванторов», а вместо этого запишем это умозаключение сразу в менее громоздком виде «на языке множеств»:
Pи 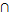 Ки
Ки 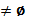
Си 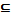 (Kи)’
(Kи)’
Фи 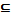 (Kи)’
(Kи)’
Фи 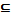 Cи (17.3’)
Cи (17.3’)
Здесь Ри - множество роз (т.е. множество истинности предиката «х – роза»);
Ки - множество красных объектов (т.е. множество истинности предиката «х – красный»);
Си - множество собак (т.е. множество истинности предиката «х – собака»);
Фи - множество фокстерьеров (т.е множество истинности предиката «х – фокстерьер»).
Все посылки нашего умозаключения (17.3), а также его вывод – истинны. Но правильна ли форма этого умозаключения? Для того чтобы получить ответ на этот вопрос, посмотрим на рис. 17.2.
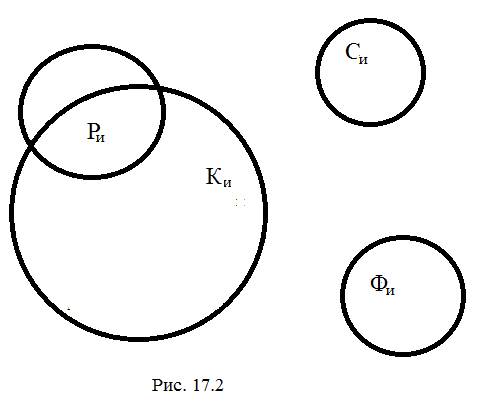
Мы видим, что все требования, которые обеспечивают истинность посылок в (17.3’), соблюдены на рис. 17.2, но ожидаемого вывода мы не получили. Это как раз и означает, что форма нашего умозаключения – неправильная.
Пример 3.
Ни одна кукушка не умеет читать
Некоторые утки умеют плавать
Некоторые утки – не кукушки (17.4)
Сразу же перепишем умозаключение (17.4) «на языке множеств»:
Ки 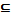 (Чи)’
(Чи)’
Уи 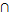 Пи
Пи 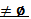
Уи 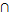 (Ки)’
(Ки)’ 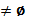 (17.4’)
(17.4’)
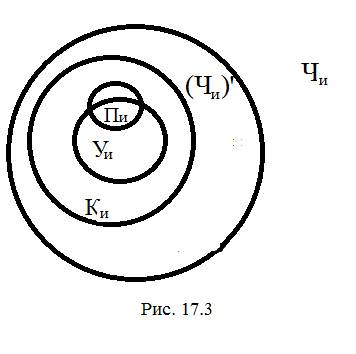
Здесь Ки – множество кукушек; Чи – множество существ, умеющих читать;
Уи – множество уток; Пи – множество существ, умеющих плавать.
Снова посылки и вывод – истинные высказывания, но, как видно из рис. 17.3, истинность посылок не обеспечивает истинность вывода. Поэтому форма умозаключения (17.4) – неправильная.
Приложение. Двенадцать иллюстраций