Зачем нужны элементы множеств, когда есть одноэлементные подмножества?
Ответ на этот вопрос заключается в следующем. Разница между элементами и подмножествами закладывает своеобразную иерархию структур в языке теории множеств. Именно эта иерархия позволяет создать гибкий математический язык, удобный для описания разнообразных задач. Следующий поясняющий пример взят из книги Ю.А. Шихановича.
Пример. Число 2 – четное, а множество {2} – одноэлементное.
Пример. Равные множества:
{a, b, c} = {c, b, a}.
Пример. Трехэлементное множество:
{a, {a}, { a, {a}}}.
Объединение множеств
Пусть А и В – два множества. Их объединением А 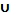 В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А, В.
В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А, В.
Из этого определения, очевидно, следует, что
А 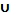 В = В
В = В 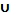 А (8.1)
А (8.1)
(коммутативность операции объединения множеств).
Справедливость соотношения (8.1) часто иллюстрируют на диаграмме Эйлера – Венна (см. рис.8.1).
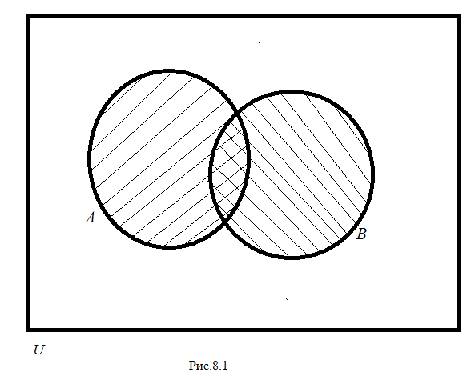
Делается это следующим образом в два этапа. 1-й этап. Вначале заштриховывают множество А, затем заштриховывают множество В. Все, что заштриховано хотя бы один раз, и есть объединение множеств А 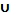 В.
В.
2-й этап. Вначале заштриховывают множество В, затем заштриховывают множество А. Все, что заштриховано хотя бы один раз, и есть объединение множеств В 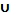 А.
А.
Как видно из рис.8.1, оба раза в результате оказывается заштрихованной (хотя бы один раз) одна и та же область. Тем самым равенство (8.1) считается доказанным.
Аналогично доказывается ассоциативность операции объединения множеств. А именно, для любых трех множеств А, В, С справедливо соотношение:
(А 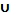 В)
В) 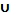 С = А
С = А 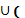 В
В 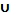 С). (8.2)
С). (8.2)
Справедливы также следующие свойства операции объединения множеств (доказательства не приводим ввиду их очевидности):
А 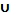 А = А,
А = А,
А 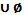 = А,
= А,
А 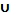 U = U.
U = U.
(Ни в коем случае не следует путать обозначение универсального множества U с обозначением операции объединения множеств 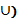
Замечание.Кроме операции объединения двух множеств, в математике используется операция одновременного объединения нескольких множеств. Пусть, например, имеются множества Аi (1 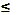 i
i 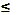 n) . Их одновременное объединение
n) . Их одновременное объединение 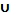 i Ai состоит из всех элементов, принадлежащих хотя бы одному из множеств Аi . Мы будем считать очевидным, что одновременное объединение трех множеств А , В , С совпадает с (8.2).
i Ai состоит из всех элементов, принадлежащих хотя бы одному из множеств Аi . Мы будем считать очевидным, что одновременное объединение трех множеств А , В , С совпадает с (8.2).
Пересечение множеств
Пусть снова А и В – два множества. Их пересечением А 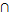 В называется множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В.
В называется множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В.
Из этого определения, очевидно, следует, что
А 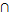 В = В
В = В 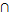 А (9.1)
А (9.1)
(коммутативность операции пересечения множеств).
Справедливость соотношения (9.1) можно проиллюстрировать на диаграмме Эйлера – Венна (см. рис.8.1). Делается это, как и в случае операции объединения множеств, в два этапа.
1-й этап. Вначале заштриховывают множество А, затем заштриховывают множество В. Все, что заштриховано дважды, и есть пересечение множеств А и В.
2-й этап. Вначале заштриховывают множество В, затем заштриховывают множество А. Все, что заштриховано дважды, и есть пересечение множеств В и А.
Как видно из рис.8.1, оба раза в результате оказывается дважды заштрихованной одна и та же область. Тем самым равенство (9.1) считается доказанным.
Аналогично доказывается ассоциативность операции пересечения множеств. А именно, для любых трех множеств А, В, С справедливо соотношение:
(А 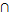 В)
В) 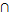 С = А
С = А 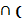 В
В 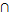 С) . (9.2)
С) . (9.2)
Справедливы также следующие очевидные свойства операции пересечения множеств (доказательства опускаем ввиду их очевидности):
А 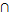 А = А,
А = А,
А 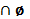 =
= 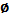 ,
,
А 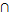 U = А.
U = А.
