Все КН для двух высказываний

Высказывания	КН

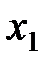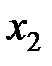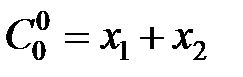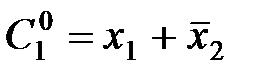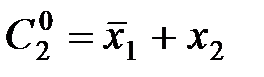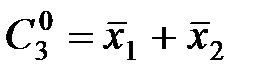2) Умеешь, могёшь

Билет 23

1) Общая запись логической функции в СКНФ. Получение аналитического выражения функции в СКНФ по таблице истинности. Пример.

Общая запись любой логической функции в СНКФ имеет вид

,

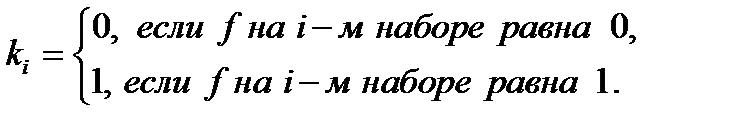
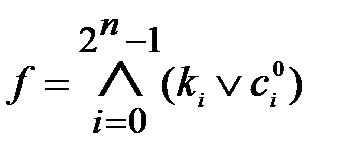Правило получения логического выражения в СНКФ из таблицы истинности, исходя из приведенной общей записи, можно сформулировать следующим образом: составить логическое произведение КН для тех наборов переменных, для которых логическая функция равна 0, причем любая переменная входит в некоторую КН со знаком отрицания, если в соответствующем наборе она равна .

2)

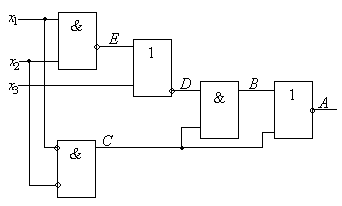
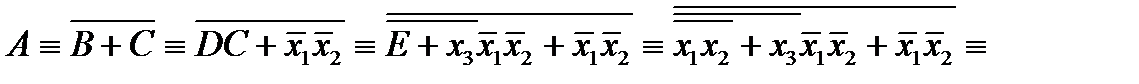
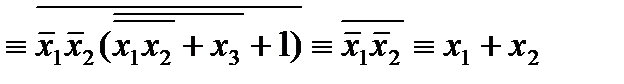
Билет 10

1. Минимизация СДНФ расчетным методом

Каждый из конкретных методов минимизации состоит из тех же трех шагов. Но эти шаги в каждом методе могут иметь свою особенность.

1.Склеивание всевозможных членов исходной СНД(К)Ф, т.е. сначала конституент, затем импликант ранга 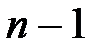и т.д., пока склеивание возможно.

2. Проверка каждой простой импликанты в сНД(К)Ф на избыточность с целью её удаления. Проверка состоит в следующем. Так как любая импликанта равна 1 для НДФ (0 для НКФ) лишь на одном наборе переменных, то если на этом наборе сумма остальных членов также обращается в 1 (0), то рассматриваемая импликанта не влияет на значение истинности данной логической функции, т.е. она является избыточной. Удаляя все такие импликанты, получим ТНД(К)Ф.

3. Упрощение полученной ТНД(К)Ф путем применения операции отрицания и распределительного закона 1-го или 2-го рода.

2. ХЗ

Билет 21

1) Логическая функция [функция алгебры логики (ФАЛ)] 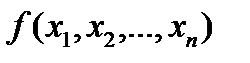– это выражение, представляющее собой сложное высказывание, состоящее из нескольких простых высказываний 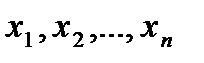,связанных соединительными словами. Это сложное высказывание принимает значения 0 или 1 на всех наборах логических значений всех простых высказываний.

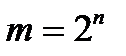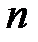Набор логических переменных, или, иначе входной набор, – это определенная комбинация значений переменных в логической функции. Максимальное число различных входных наборов есть величина , где –число переменных.

Полностью определенная функция – это логическая функция, принимающая значение 0 или 1 на всех входных наборах.

Частично определенная функция – это логическая функция, значения которой определены не на всех входных наборах. Такие наборы называют безразличными.

НДФ – это дизъюнкция нескольких элементарных конъюнкций. Эта форма называется нормальной, так как все ее члены имеет вид элементарных конъюнкций.

Общая запись любой логической функции в СНДФ имеет вид

,

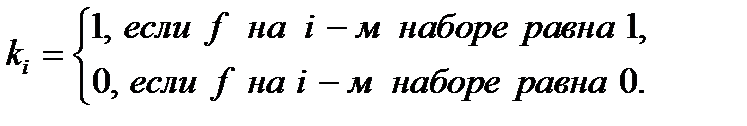
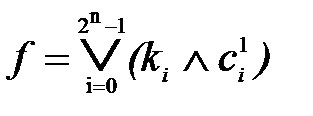
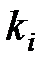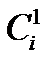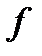Иначе говоря, значение определяет факт вхождения в . При 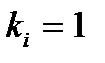конституента 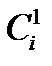входит в 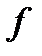, а при 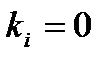– не входит.

Пример. По заданной таблице истинности составить СНДФ функций

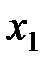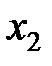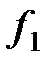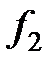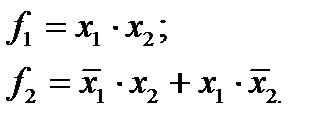
Общая запись любой логической функции в СНКФ имеет вид

,

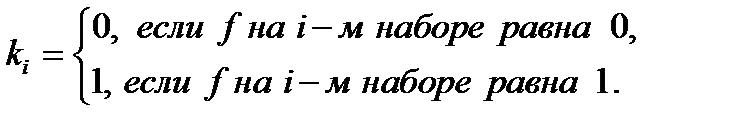
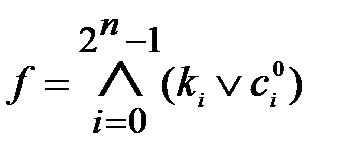Иначе говоря, в СНКФ будет отсутствовать тот дизъюнктивный член, для которого 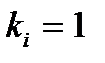.