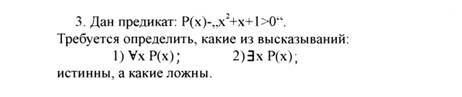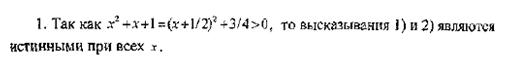Назначение исчисления высказываний и отличие от алгебры логики.

Назначение исчисления высказываний и отличие от алгебры логики.

Исчислением называют составную часть некоторых разделов математики, трактующих правила вычислений и оперирования с объектами того или иного типа. Например, говорят о дифференциальном, интегральном, вариационном и т.д. исчислениях.

В исчислении высказываний объектами исследований являются высказывания. Их исчисление служит для формализации способов логических рассуждений, в которых учитывается лишь логическая структура высказываний, а именно: как одни высказывания получены из других с помощью таких логических операций, как отрицание, конъюнкция дизъюнкция и импликация. Обратим внимание, что сюда не входит операция эквиваленции. В одних литературных источниках данную операцию в этот список включают, в других – нет (например, в математической энциклопедии эта операция в список не включена).

В алгебре логики (высказываний) мы под термином “высказывание” понимали любое повествовательное предложение, о котором можно было сказать, истинно оно или ложно. При этом мы испытывали затруднения, когда вставал вопрос о том, считать ли некоторое повествовательное предложение высказыванием, если о его истинности или ложности нельзя было сказать ничего определенного. Поэтому очевидно, что для построения логической теории, которая позволяла бы формализовать процесс получения одних высказываний из других, пользоваться понятиями истинности

2. Определение формулы исчисления высказываний, примеры формул и примеры предложений, не являющихся формулами

Дадим теперь определение формулы исчисления высказываний:

1) всякое переменное 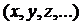или постоянное 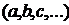высказывание является формулой,

2) если А и В – формулы, то предложения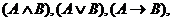

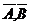– также формулы,

3) никакая другая последовательность символов не является

формулой.

Таким образом, есл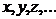и и 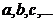– формулы, то предложения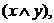 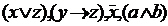– тоже формулы. Формулами будут также предложения 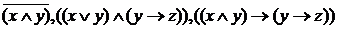Очевидно, что предложения 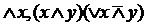не являются формулами.

Понятие об аксиоме. Система аксиом.

аксиома – это некоторое исходное положение, принимаемое в данной науке без доказательства

Исчисление высказываний опирается на 11 аксиом и 2 простейших правила вывода. Все аксиомы являются правильными сложными высказываниями. Они разделены на 4 группы.

Система аксиом исчисления высказываний

Первая группа аксиом:

I₁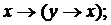

I₂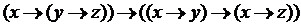

Вторая группа аксиом:

II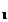

II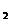

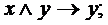
II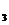

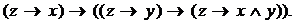
Третья группа аксиом:

II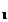

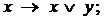
II

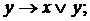
II

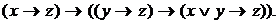
Четвертая группа аксиом:

IV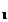

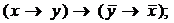
IV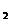

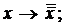
IV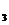

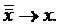
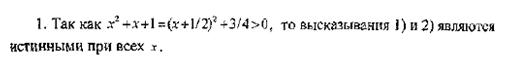
Тогда правило подстановка схематически запишется так

.

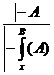Читается эта запись следующим образом: “Если формула 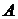доказуема, то доказуема и формула ”.

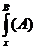2.Правило заключения (ПЗ – modus ponens)

Если формулы 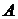и 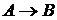доказуемы в исчислении высказываний, то формула 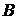также доказуема. Схематическая запись этого правила имеет вид

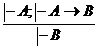
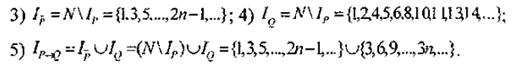
Понятие предиката, определённого одноместного предиката. Множество истинности предиката. Тождественно истинный предикат. Примеры предикатов.

Логика предикатов расчленяет простое высказывание на субъект (подлежащее, дополнение) и предикат (сказуемое, определение).

Субъект – это то, о чем что-то утверждается в высказывании. Предикат – это то, что именно утверждается о субъекте. Например, в высказывании “12 – составное число” “12” – субъект, “ составное число” – предикат. Это высказывание утверждает, что “12” обладает свойством быть составным числом.

Определение 1. Одноместным предикатом 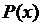называется произвольная функция переменной 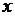, определенная на некотором множестве 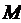и принимающая значения из множества .

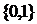Множество 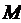, на котором определен предикат 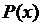, называется областью определения предиката.

Множество всех элементов 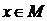, при которых предикат 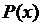принимает значение “истина”, называется множеством истинности этого предиката. Символически множество истинности предиката 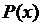записывают так: 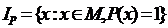. Эта запись означает, что множество 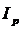состоит из элементов, обладающих свойством, указанным после двоеточия.

Определение 2.Предикат 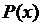, определенный на множестве 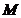, называется тождественно истинным (тождественно ложным), если .

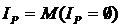Обобщением понятия одноместного предиката является понятие 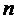-местного предиката, с помощью которого выражается отношение между 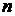предметами.

Понятие Н местного предиката. Двухместного предиката. Пример бинарного предиката. Декартово произведение 2 множеств.

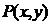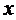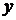Определение 3. Двухместным предикатом называется функция двух переменных и , определенная на множестве 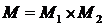и принимающая значение из множества 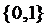. Примерами двухместных предикатов являются: предикат равенства 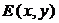─ “ 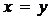”, определенный на множестве действительных чисел 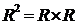, предикат делимости нацело 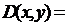” ”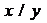, определенный на множестве .

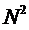Таким образом, предикат – это функция или, как мы уже говорили выше, высказывательная форма. Если, например, в высказывательную форму 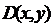мы подставим вместо 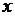и 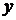какие-то конкретные значения, то высказывательная форма становится высказыванием, принимающим вполне определенные значения истины или лжи (1 или 0). Так, 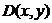есть предикат (высказывательная форма), но 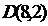уже является истинным высказыванием, а 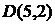− ложным высказыванием. В то же время 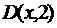является высказывательной формой (предикатом), так как его значение истинности зависит от того, каким натуральным числом будет заменена переменная 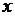(т.е. является функцией от 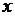, а значит, предикатом). В то же время 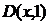является высказыванием, причем истинным, так как любое 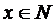делится на единицу.

Еще несколько замечаний о терминологии. Иногда вместо термина “ 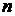-местный предикат” употребляют термин “ 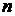-арный предикат”. При 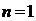этот предикат называется унарным (от лат. unio ─ единение, единый), при 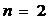− бинарным (от лат. binaries − двойной) и при 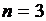− тернарным (от лат. tertia – третья).

Для общности еще вводят понятие 0-арного предиката, под которым понимается любое истинное или ложное высказывание. Такое определение логично, если вспомнить, что в определении высказывания нет переменной, а в определении предиката она есть. Тогда некоторое предложение мы можем называть 0-арным предикатом, если в нем отсутствуют переменные.

Дизъюнкция импликация

Дизъюнкцией двух предикатов 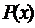и 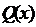называется новый предикат 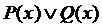, который принимает значение “ложь” при тех значениях 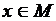, при которых каждый из предикатов принимает значение “ложь”, и принимает значение “истина” во всех остальных случаях.

Очевидно, что множеством истинности предиката 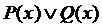является объединение множеств истинности предикатов 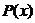и 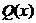, т.е. 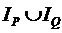. Так, для тех же предикатов, что и в выше приведенном примере, их дизъюнкцией 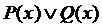будет предикат “ 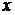−четное число или 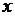кратно 5”, множество истинности которого есть .

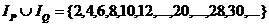Импликацией предикатов 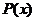и 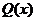называется новый предикат 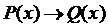, который является ложным при тех значениях 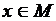, при которых предикат 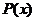принимает значение “истина”, а предикат 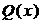− значение “ложь” и принимает значение “истина” во всех остальных случаях.

Множество истинности этой импликации определяется из следующих рассуждений: 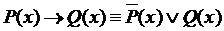следовательно .

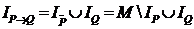Так, для предикатов 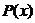− “ 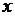кратно 4” и 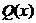− “ 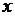– четное число”, определенных на 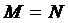, импликацией 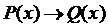является предикат словесная формулировка которого будет: “если 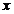кратно 4, то 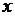– четное число. Так как 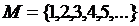, ,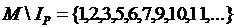то 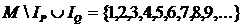т.е. все натуральные числа.

Назначение исчисления высказываний и отличие от алгебры логики.

Исчислением называют составную часть некоторых разделов математики, трактующих правила вычислений и оперирования с объектами того или иного типа. Например, говорят о дифференциальном, интегральном, вариационном и т.д. исчислениях.

В исчислении высказываний объектами исследований являются высказывания. Их исчисление служит для формализации способов логических рассуждений, в которых учитывается лишь логическая структура высказываний, а именно: как одни высказывания получены из других с помощью таких логических операций, как отрицание, конъюнкция дизъюнкция и импликация. Обратим внимание, что сюда не входит операция эквиваленции. В одних литературных источниках данную операцию в этот список включают, в других – нет (например, в математической энциклопедии эта операция в список не включена).

В алгебре логики (высказываний) мы под термином “высказывание” понимали любое повествовательное предложение, о котором можно было сказать, истинно оно или ложно. При этом мы испытывали затруднения, когда вставал вопрос о том, считать ли некоторое повествовательное предложение высказыванием, если о его истинности или ложности нельзя было сказать ничего определенного. Поэтому очевидно, что для построения логической теории, которая позволяла бы формализовать процесс получения одних высказываний из других, пользоваться понятиями истинности

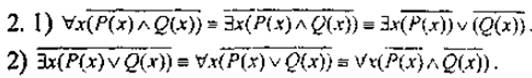
2. Определение формулы исчисления высказываний, примеры формул и примеры предложений, не являющихся формулами

Дадим теперь определение формулы исчисления высказываний:

1) всякое переменное 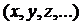или постоянное 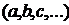высказывание является формулой,

2) если А и В – формулы, то предложения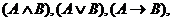

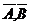– также формулы,

3) никакая другая последовательность символов не является

формулой.

Таким образом, есл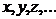и и 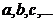– формулы, то предложения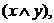 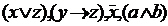– тоже формулы. Формулами будут также предложения 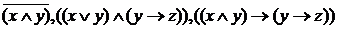Очевидно, что предложения 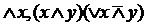не являются формулами.