Отношения между простыми суждениями.

При отношениях эквивалентностимежду простыми суждениями одна и та же мысль выражается различными словами, суждения имеют одинаковые логические характеристики. Например, “Некоторые дни мая были дождливыми” и “В отдельные майские дни шел дождь”.

Для удобства запоминания остальных видов логических отношений между суждениями в логике употребляют “логический квадрат”.Его вершины обозначают четыре вида простых суждений А, I, Е, О. Стороны и диагонали обозначают различные виды отношений между суждениями.

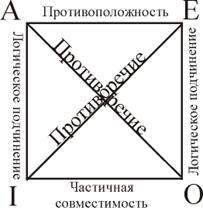При отношениях логического подчинения истинность подчиняющего суждения предполагает истинность подчиненного, а ложность подчиненного - ложность подчиняющего. Схемы вывода по логическому квадрату (для подчинения):

Аи®Iи ; Eи®Oи; Iл®Ал; Ол®Ел;

Ал®I?; Iи®А?; Ел®О?; Ои®Е?;

Ложность подчиняющего суждения или истинность подчиняемого оставляют логическое значение другого суждения неопределённым. Например, “Все люди смертны” – истинно (Аи), значит “Некоторые люди смертны” (Iи) – тоже истинно. “Ни один человек не является мудрым” - ложно (Ел), а “Некоторые люди не являются мудрыми” – неопределённо(О?).

При отношениях субконтрарности оба суждения могут быть одновременно истинными, но не могут быть одновременно ложными.

Iл®Oи; Ол®Iи; Iи®О?;Ои®I?.

При отношениях противоположности суждения не могут быть одновременно истинными, но могут быть одновременно ложными.

Аи®Ел; Еи®Ал;. Ал®Е? Ел® А?

При отношениях противоречиясуждения не могут быть одновременно ни истинными, ни ложными. Если одно из них истинно, другое необходимо ложно, и наоборот.

Аи®Ол; Ои®Ал; Еи®Iл; Iи®Ел;

Ал®Ои; Ол®Аи; Ел®Iи; Iл®Еи;

Например, “Некоторые юристы – адвокаты” – частноутвердительное, истинно. Противоречащее ему – общеотрицательное “Ни один юрист не является адвокатом” - ложно.

Отношения между сложными суждениями.

Отношения между сложными суждениями подобны отношениям между простыми суждениями. Логические отношения между сложными суждениями определяются при помощи таблиц истинности. Для этого сравниваемые высказывания записываются на языке логики высказываний, строится таблица истинности для полученных формул, затем определяется вид отношений между суждениями.

Если в таблицах есть строка, в которой все формулы имеют значение “истинно”, то они совместимы по истинности. При наличии строки, в которой все формулы имеют значение “ложно”, они совместимы по ложности.

При отношениях эквивалентности, значения в строках должны совпадать и по истинности, и по ложности. При отношениях частичной совместимости, значения в одних строках совпадают по истинности, а в других – несовместимы. При отношении подчинения (следования), из истинного значения подчиняющего суждения не должно следовать ложное значение подчиненного суждения. При отношениях противоположности значения в некоторых строках совпадают по ложности, в других – несовместимы. При отношениях противоречия значения ни в одной строке не должны соответствовать ни по истинности, ни по ложности.

Например, “Если Пирр выиграл сражение, то он победил в войне” и “Пирр выиграл сражение, но не победил в войне”.

Записываем суждения в символической форме: а®в; аÙùв.

Строим таблицу:

а	в	ùв	а®в	аÙùв
и	и	л	и	л
и	л	и	л	и
л	и	л	и	л
л	л	и	и	л

Сравнение строк истинности в двух последних столбцах показывает, что суждения несовместимы ни по истинности, ни по ложности. Следовательно, суждения находятся в отношении противоречия.

Модальные суждения

Модальные суждения - это суждения, содержащие некоторую дополнительную информацию; включают в свой состав слова, придающие суждению дополнительную информацию - модальные операторы: возможно, необходимо и т.д.

Модальные суждения бывают простые и сложные. Символически могут быть представлены следующим образом: Mp – простое суждение «Возможно, этой зимой вырастут цены на продовольствие»; M (pÚq) – сложное суждение “ Доказано, что Рябов или Зайцев причастны к преступлению”.