Усеченное нормальное распределение
При нормальном (гауссовом) распределении случайной величины она может принимать любые значения от –∞ до +∞. Поскольку возможные значения случайной наработки до отказа Т могут быть только положительными, распределение Т может быть лишь усеченным нормальным.
Усеченным нормальным распределением случайной величины называется распределение, получаемое из нормального при ограничении интервала возможных значений этой величины. Так как возможные значения случайной величины Т ограничены интервалом (t1, t2), то плотность усеченного распределения
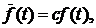
где
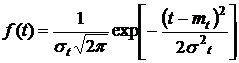 (15)
(15)
f(t) – плотность неусеченного распределения; с – нормирующий множитель, находимый из условия, что площадь под кривой распределения равна единице, т. е.
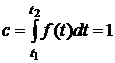
или
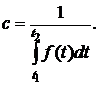 (16)
(16)
Подставив в (16) выражение для f(t) и применив подстановку
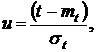
где mt, σt – среднее значение и среднее квадратическое отклонение неусеченного распределения, после преобразования получим:
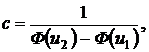 (17)
(17)
где 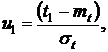
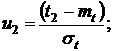
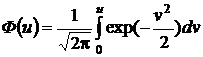 – нормированная функция Лапласа.
– нормированная функция Лапласа.
Функция надежности
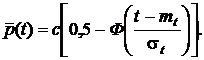 (18)
(18)
Интенсивность отказов
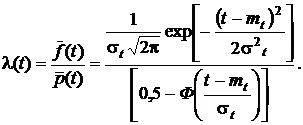
Найдем формулы для числовых характеристик усеченного нормального распределения: математического ожидания наработки до отказа 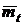 и дисперсии наработки до отказа
и дисперсии наработки до отказа 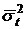 . Согласно определениям этих характеристик имеем
. Согласно определениям этих характеристик имеем
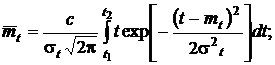 (19)
(19)
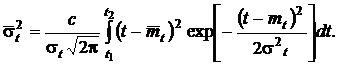 (20)
(20)
Проведя преобразования, получим:
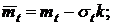 (21)
(21)
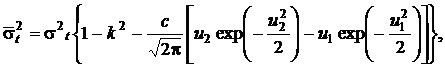 (22)
(22)
где
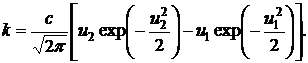 (23)
(23)
Когда возможные значения случайной величины Т лежат в интервале (0, ∞), из формул (17), (19) – (23) получаем:
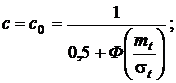 (24)
(24)
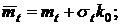 (25)
(25)
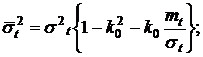 (26)
(26)
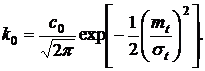 (27)
(27)
На рис. 6 приведены зависимости отношений числовых характеристик усеченного и неусеченного нормального распределений и значения нормирующего множителя c0от отношения mt /σt.
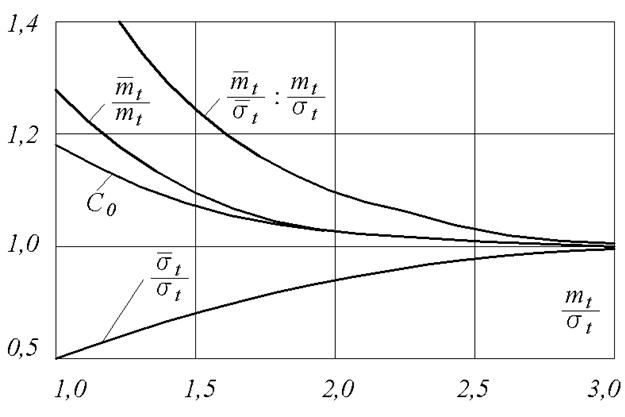
Рис. 6. Зависимость отношений числовых характеристик усеченного и неусеченного нормального распределения и нормирующего множителя c0 от отношения mt/σt. (Черта над  ,
, 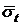 означает, что эти характеристики относятся к усеченному распределению)
означает, что эти характеристики относятся к усеченному распределению)
Изрис. 6 следует, что при mt /σt >2, что обычно и имеет место на практике при употреблении нормального распределения, значение c0 очень мало отличается от единицы и 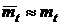 ,
, 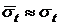 . Поэтому в дальнейшем не будем добавлять термин «усеченное» к названию «нормальное распределение наработки до отказа».
. Поэтому в дальнейшем не будем добавлять термин «усеченное» к названию «нормальное распределение наработки до отказа».
Необходимо отметить, что вопреки распространенному мнению при отказах элементов за счет износа распределение наработки до отказа будет далеко не всегда нормальным. Необходимым условием нормального распределения наработки до отказа является малый разброс значений скорости износа элементов.
Ввиду большого теоретического и прикладного значения нормального распределения его стараются иногда применить и при явно несимметричных распределениях наработки до отказа. Для этого подбирают некоторую функцию случайной наработки до отказа, напримерlgT, T2 и т. д., приближенно следующую нормальному закону. Например, довольно часто используется логарифмически нормальное распределение усталостной долговечности, при котором предполагается, что логарифм числа циклов нагрузки до разрушения образца распределен по нормальному закону.
Распределение Релея
Для распределения Релея:
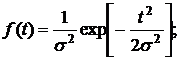
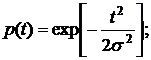
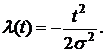
Параметр распределения Релея, обычно обозначаемый σ, является модой этого распределения. Его не нужно смешивать со средним квадратическим отклонением σt . Для распределения Релея математическое ожидание
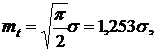
а дисперсия
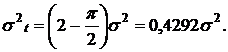
Гамма-распределение
Плотность гамма-распределения
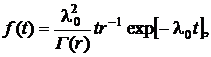 (28)
(28)
где 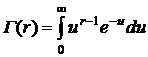 – гамма-функция.
– гамма-функция.
В теории надежности гамма-распределение обычно используется при целом r. При r=1 получается показательное распределение. В данном случае показательное распределение – это распределение наработки до первого отказа. При целом r>1 гамма-распределение является распределением суммы r независимых случайных величин, каждая из которых имеет показательное распределение с параметром 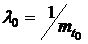 . Гамма-распределение при целом r иногда называют распределением Эрланга. Для такого распределения
. Гамма-распределение при целом r иногда называют распределением Эрланга. Для такого распределения
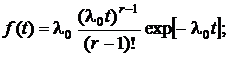 (29)
(29)
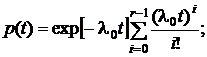 (30)
(30)
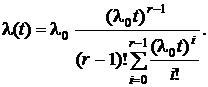 (31)
(31)
Матёматическое ожидание наработки до отказа
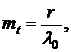
дисперсия
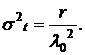
Графики гамма-распределения приведены на рис. 7.
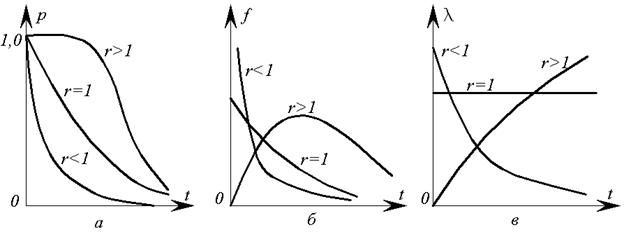
Рис. 7. Графики гамма-распределения. а – функции надежности; б – кривые распределения наработки до появления r отказов; в – интенсивности отказов.
При больших r гамма-распределение сходится, к нормальному распределению с параметрами
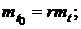
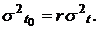
В качестве примера использования гамма-распределения представим себе резервированную систему, состоящую из r одинаковых элементов, причем под нагрузкой находится один элемент, а остиальные поочередно автоматически включаются в работу после отказа работающего элемента. При показательном распределении наработки до отказа элементов суммарная наработка системы будет подчинена гамма-распределению.
Распределение Вейбулла
Кривые этого распределения приведены нарис 1.8. Плотность распределения Вейбулла равна:
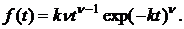 (32)
(32)
Распределение Вейбулла имеет два параметра: к и ν. Параметр к определяет масштаб; при его изменении кривая распределения сжимается или растягивается.
При ν =1 распределение Вейбулла превращается в показательное распределение. Обычно значение ν выбираются в пределах от 1 до 2.
Для распределения Вейбулла функция надежностиp(t) иинтенсивность отказов λ(t) выражается формулами:
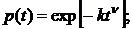 (33)
(33)
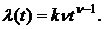 (34)
(34)
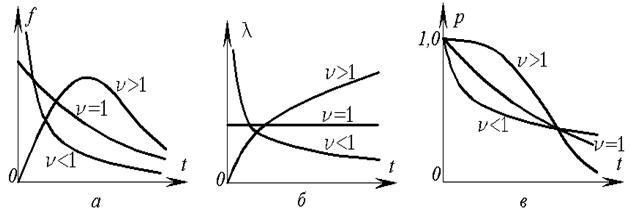
Рис. 8. Графики распределения Вейбулла при k = 1: а – кривые распределения; б – интенсивности отказов; в – функции надежности.
Математическое ожидание наработки отказа
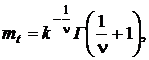
где 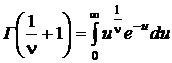 – гамма-функция.
– гамма-функция.
Распределение Вейбулла иногда используется для описания надежности шариковых подшипников и некоторых типов электронных ламп (ν=1,4 – 1,7).
Треугольное распределение
Треугольное характеризует случайные величины, имеющие ограниченную область возможных значений (tн, tk). Положение и форму треугольного распределения характеризуют три параметра: tн, tk – границы области возможных значений; tм – мода (рис. 9).
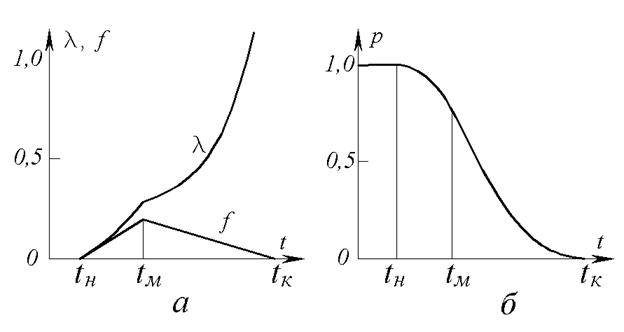 Рис. 9. Треугольное распределение случайной величины: a – графики плотности распределения f(t) и интенсивности отказов; λ(t); б – график функции надежности p(t)
Рис. 9. Треугольное распределение случайной величины: a – графики плотности распределения f(t) и интенсивности отказов; λ(t); б – график функции надежности p(t)
Если обозначить значение плотности распределения в точке моды f(tм)=h, тo 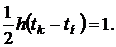
Плотность распределения
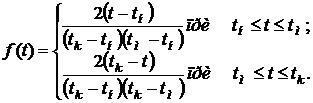
Функция надежности
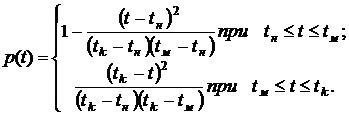
Интенсивность отказов
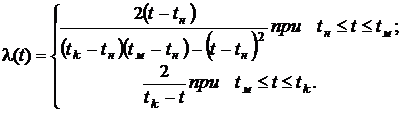
В некоторых задачах удобно использовать в качестве параметров распределения также скорости изменения плотности распределения
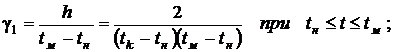
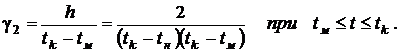
Медиана tме треугольного распределения может быть найдена из уравнения
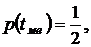
в результате решения которого получим
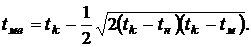
Математическое ожидание
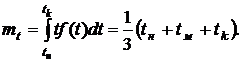 (35)
(35)
Применив подстановку 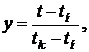 можно перейти к нормированному треугольному распределению. При этом tн соответствует yн = 0, tkсоответствует yk = 1.
можно перейти к нормированному треугольному распределению. При этом tн соответствует yн = 0, tkсоответствует yk = 1.
Обозначим:
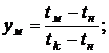
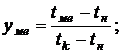
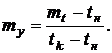
После преобразований получим:
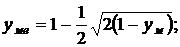
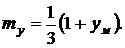
Функция надежности может быть выражена через вспомогательную функцию ФΔ(y).следующим образом:
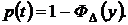 (36)
(36)
где ФΔ(y) – нормированная функция распределения;
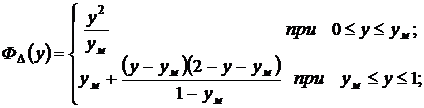 (37)
(37)
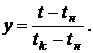
На рис. 10 приведены графики ФΔ (y) при различных значения параметра yм. Значения функции ФΔ(y) надежности, соответствующие определенным tн, tм, tк, можно также вычислить но табл. 1.
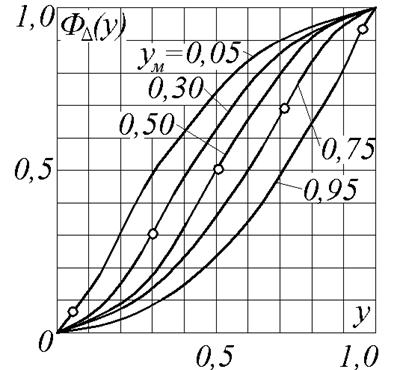
Рис.1.10. Значения нормированной функции распределения ФΔ (y). Точками на кривых отмечены значения ФΔ(y)= yм
Таблица 1
| у | yм | ||||||||||
| 0,05 | 0,10 | 0,20 | 0.30 | 0,40 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 0,95 | |
| 0,05 | 0,050 | 0,025 | 0,012 | 0,008 | 0,007 | 0,005 | 0,004 | 0,034 | 0,003 | 0,003 | 0,003 |
| 0,10 | 0,147 | 0,100 | 0,050 | 0,033 | 0,025 | 0,020 | 0,017 | 0,014 | 0,013 | 0,011 | 0,011 |
| 0,20 | 0,326 | 0,289 | 0,200 | 0,133 | 0,100 | 0,080 | 0,067 | 0,057 | 0,050 | 0,044 | 0,042 |
| 0,30 | 0,484 | 0,456 | 0,387 | 0,300 | 0,225 | 0,180 | 0,150 | 0,129 | 0,113 | 0,100 | 0,095 |
| 0,40 | 0,621 | 0,400 | 0,560 | 0,486 | 0,400 | 0,320 | 0,267 | 0,229 | 0,200 | 0,178 | 0,168 |
| 0,50 | 0,737 | 0,722 | 0,688 | 0,643 | 0,583 | 0,500 | 0,417 | 0,357 | 0,313 | 0,278 | 0,263 |
| 0,60 | 0,832 | 0,822 | 0,800 | 0,771 | 0,733 | 0,680 | 0,600 | 0,514 | 0,450 | 0,400 | 0,379 |
| 0,70 | 0,905 | 0,900 | 0,888 | 0,871 | 0,850 | 0,820 | 0,775 | 0,700 | 0,613 | 0,544 | 0,516 |
| 0,80 | 0,978 | 0,956 | 0,950 | 0,943 | 0,933 | 0,920 | 0,900 | 0,867 | 0,800 | 0,711 | 0,674 |
| 0,90 | 0,989 | 0,969 | 0,987 | 0,986 | 0,983 | 0,980 | 0,975 | 0,937 | 0,950 | 0,900 | 0,853 |
| 0,95 | 0,997 | 0,997 | 0,997 | 0,996 | 0,996 | 0,995 | 0,993 | 0,992 | 0,988 | 0,975 | 0,950 |
