Выполнимость. общезначимость

Формула есть перевод содержательного рассуждения в формальное рассуждение. Формула имеет смысл только тогда, когда имеется какая-нибудь интерпретация входящих в нее символов. Каждая интерпретация состоит в указании множества М изменения предметных переменных и задании отношения между переменными с помощью предикатов.

Для данной интерпретации формула представляет собой высказывание, если переменные связаны кванторами, а если есть свободные переменные, то формула есть предикат, который может быть истинным для одних значений переменных из области интерпретации и ложным для других.

Пример 2.22.

Пусть М – множество целых положительных чисел, и дан предикат A(x, y) = “x y”.

Рассмотрим следующие формулы:

1)A(x, y);

2) "yA(x, y);

3) $x"yA(x, y).

Первая формула – это предикат, который является истинным высказыванием для всех пар целых положительных чисел (a, b), таких, что a b.

Вторая формула – предикат “Для всякого целого положительного числа y имеет место x y”, который является истинным только для x = 1.

Третья формула – высказывание “Существует такое x, что для всякого y имеет место x y”. Оно является истинным и соответствует тому, что на множестве М есть наименьшее число (единица).

Пусть задаио множество M изменения предметных переменных формулы A(x₁, x₂, ... , x_n), т. е. (x₁, x₂, ... , x_n) 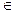M.

Определение 2.7. Формула A называется выполнимой в данной интерпретации, если существует набор значений переменных (a₁, a₂, ... , a_n) 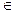M, для которого A(a₁, a₂, ... , a_n) = И.

Определение 2.8. Формула A называется истинной в данной интерпретации, если A(x₁, x₂, ... , x_n) = И на любом наборе своих переменных (x₁, x₂, ... , x_n) 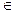M.

Определение 2.9. Формула A называется общезначимой или тождественно-истинной, если она истинна в каждой интерпретации.

Определение 210. Формула A называется выполнимой, если существует интерпретация, для которой она выполнима.

Проблема разрешимости для логики предикатов, так же, как и для логики высказываний (см. раздел 1.5) заключается в том, чтобы установить, является ли произвольная формула тождественно-истинной.

Но, если для логики высказываний эта проблема решается положительно, то для логики предикатов неразрешимость этой проблемы устанавливает следующая теорема:

Теорема 2.4.(Теорема Черча). Не существует алгоритма, который для любой формулы логики предикатов устанавливает, общезначима она или нет.

Однако, для одноместных предикатов проблема разрешимости решается положительно.

В общем случае выделение общезначимых формул логики предикатов возможно в рамках аксиоматического подхода, который будет рассмотрен ниже (см. раздел 3.3).

Контрольные вопросы к теме 2

1. Какие из следующих утверждений верны:

а) Предикат есть сложное высказывание, состоящее из простых высказываний.

б) Предикат есть высказывание, зависящее от параметров.

в) Высказывание есть 0-местный предикат.

г) Высказывание есть одноместный предикат.

2. Выберите правильный вариант ответа 1 – 4 для следующих вопросов:

а) Обобщением какой операции является связывание квантором общности?

б) Обобщением какой операции является связывание квантором существования?

Варианты ответа: 1 – дизъюнкция; 2 – конъюнкция; 3 – импликация; 4 – эквивалентность.

3. Какие из следующих формул логики предикатов являются равносильными:

а) "xA(x) и $x(A(x)); б) $xA(x)) и $xA(x)); в)"x(A(x)ÚB) и "xA(x)ÚB;

г) $x(A(x)&B(x)) и $xA(x)&$xB(x); д)"x"yA(x,y) и "y"xA(x,y);

е) $x$yA(x, y) и $y$xA(x, y);

ж) $x"yA(x, y) и "y$xA(x, y).

4. Какие из следующих формул логики предикатов являются приведенными и какие – нормальными:

а) "xA(x) Ú $x"yA(x, y); б) $y$xA(x, y)& "y$zB(y, z); в) $x"y$z(A(x, y) & B(y, z)).