Определение предиката. Кванторы

Определение 2.1. Предикатом P(x₁, x₂, ... , x_n) называется функция, аргументы которой определены на некотором множестве М, x₁, x₂, ... , x_n 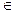M, а сама она принимает два значения: И (истина) и Л (ложь). Таким образом, предикат осуществляет отображение М 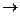{И, Л}.

Переменные x₁, x₂, ... , x_n называются предметными переменными, а множество M – предметной областью.

Если все переменные x₁, x₂, ... , x_n принимают конкретные значения, то предикат есть не что иное, как высказывание, Таким образом, высказывание является частным случаем предиката. Можно сказать, что предикат есть высказывание, зависящее от параметров.

Пример 2.1.

а) P(x) = “x – четное число”. Здесь М – множество целых чисел, x 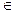M.

б) A(x, y, z) = “x, y, z лежат на одной окружности”. Здесь М – множество точек плоскости, x, y, z 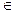M

в) B(x, y) = “x старше y”. Здесь M – множество людей, x, y 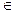M.

Предикат от n переменных называется n-местным предикатом. Высказывание есть 0-местный предикат.

Как видно из примера 2.1, одноместный предикат отражает свойство некоторого объекта, а многоместный предикат выражает отношение между многими объектами.

Над предикатами можно производить обычные логические операции и получать при этом другие предикаты. Таким образом можно говорить об алгебре предикатов.

Пример 2.2.

Пусть A(x) – предикат “x делится на 3”, а B(x) – предикат “x делится на 2”. Тогда A(x) Ú B(x) – предикат “x делится на 3 или на 2”, а A(x) & B(x) – предикат “x делится на 3 и на 2”.

Кроме операций логики высказываний, в логике предикатов используются особые логические символы – кванторы (были введены немецким математиком Г. Фреге).

Квантор общности. Пусть P(x) – некоторый предикат, определенный для каждого x Î М. Тогда выражение "xP(x) является истинным высказыванием, если P(x) истинно для всякого x Î М и ложным в противном случае. Символ "x называется квантором общности. Выражение "xP(x) читается: “Для всех x имеет место P(x)”. В обычной речи квантору общности соответствуют слова: все, всякий, каждый, любой. Возможно отрицание квантора общности: Ø"xP(x): “Не для всех x имеет место P(x)”.

Пример 2.3.

Пусть P(x) – предикат “x – четное число”. Тогда "xP(x) есть высказывание “Всякое x – четное число" = “Все числа – четные", которое истинно на множестве M четных чисел и ложно, если М содержит хотя бы одно нечетное число, например, если M – множество целых чисел. Отрицание Ø"xP(x) есть высказывание “Не всякое x – четное число" = “Не все числа – четные", которое истинно на множестве целых чисел и ложно на множестве четных чисел.

Квантор существования. Пусть P(x) – некоторый предикат, x Î М. Тогда выражение $xP(x) является истинным высказыванием, если P(x) истинно хотя бы для одного x Î М и ложным в противном случае. Символ $x называется квантором существования. Выражение $xP(x) читается: “Существует x, для которого имеет место P(x)”. В обычной речи квантору существования соответствуют слова: некоторый, несколько. Возможно отрицание квантора существования: Ø$xP(x): “Не существует x, для которого имеет место P(x)”.

Кванторы существования и общности называются двойственными кванторами.

Пример 2.4.

Пусть, как и в примере 2.3, P(x) – предикат “x – четное число”. Тогда $xP(x) есть высказывание “Некоторые x – четные числа” = “Существуют четные числа”, которое истинно на множестве M, содержащем хотя бы одно четное число и ложно, если М содержит только нечетные числа. Высказывание Ø$xP(x) = “Неверно, что некоторые x – четные числа” = “Не существует четных чисел” истинно на множестве M, содержащем только нечетные числа и ложно, если М содержит хотя бы одно четное число.

Буква x, стоящая справа от квантора, называется кванторной переменной и должна присутствовать обязательно. Переменная, стоящая под знаком квантора, называется также связанной переменной. Несвязанная переменная называется свободной. Выражения"xP(x) и $xP(x) не зависят от x и имеют вполне определенные значения. Поэтому переименование связанной переменной, т. е. переход, например, от выражения "xP(x) к "yP(y) не меняет его истинностного значения.

Кванторы могут применяться и к многоместным предикатам. При этом число свободных переменных уменьшается на единицу. Одноместный предикат при связывании переменной квантором становится 0-местным предикатом, т. е. высказыванием.