Тема 1. Предмет и значение логики

СОДЕРЖАНИЕ

1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

2. ТЕМАТИЧЕСКИЙ ПЛАН КУРСА.

3. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ..

4. ТЕОРЕТИЧЕСКИЕ МАТЕРИАЛЫ ПО КУРСУ.

5. ПЛАНЫ ПРАКТИЧЕСКИХ (СЕМИНАРСКИХ) ЗАНЯТИЙ.

6. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ И ОБРАЗЦЫ ВЫПОЛНЕНИЯ ЗАДАНИЙ.

7. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ..

8. ТЕСТЫ ДЛЯ САМОПРОВЕРКИ.

9. КОНТРОЛЬНЫЕ ВОПРОСЫ ПО КУРСУ «ЛОГИКА».

10. ПРИМЕРНАЯ ТЕМАТИКА РЕФЕРАТОВ.

11. ЛИТЕРАТУРА ПО ДИСЦИПЛИНЕ.

1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Логические знания чрезвычайно важны для повышения эффективности мыслительной деятельности человека, для предотвращения логических ошибок. Логика в значительной мере способствует формированию умения качественно работать с огромным количеством информации. Запас логических знаний, определенная логическая подготовка особенно необходимы юристу – он должен научиться творчески мыслить, овладеть логическими основами аргументации, теорией форм правильных рассуждений.

Цель преподавания курса логики – ознакомить студентов с различными логическими действиями и операциями.

Главная дидактическая цель данного учебно-методического комплекса состоит в том, чтобы углубить знания будущего специалиста в области правоведения о теоретических и прикладных аспектах логики, и вооружить его знаниями, которые позволили бы решить следующие задачи:

· лучше ориентироваться в функциях, выполняемых различными элементами разговорного и научного языка в отдельных коммуникативно-познавательных ситуациях,

· эффективно использовать логические законы как средства убеждения, как инструменты контроля за правильностью самых разнообразных рассуждений,

· уверенно и грамотно выполнять такие логические процедуры, как обобщение и ограничение понятий, определение, деление, преобразование высказываний, установление их истинности (ложности) на основе знаний об истинности (ложности) других высказываний и др.,

· уметь выявлять логические противоречия, умышленные и непроизвольные погрешности в рассуждениях, некорректные приемы в дискуссиях и спорах,

· осознанно использовать логические приемы в различных коммуникативных ситуациях,

· четче представлять структуру нормативных правовых актов, устанавливать наиболее общие связи и отношения между ними,

· обнаруживать возможности применения методов, пригодных для изучения одних обстоятельств в других коммуникативных ситуациях.

Освоение курса, обобщающего теоретические и практические вопросы логики, требует серьезной и вдумчивой работы. Предложенные теоретические материалы и практические задания позволят выработать навыки логического анализа рассуждений, производимых как в письменной, так и в устной речи; могут быть использованы при проведении семинарских занятий, а также для организации самостоятельной работы студентов по учебной дисциплине «Логика».

Для проверки знаний студентам предлагаются проверочные и контрольные вопросы и задания, включенные в качестве обязательного элемента при проверке практических умений по изучаемой дисциплине.

ТЕМАТИЧЕСКИЙ ПЛАН КУРСА

Раздел, тема	Количество часов
Всего	В том числе на практические занятия
Введение
Раздел 1. Логическая теория высказываний 2.1. Виды высказываний. 2.2. Законы логики высказываний. 2.3. Отношения между логическими формами высказываний. 2.4. Табличный способ анализа рассуждений в логике высказываний.
Раздел 2. Логическая теория имён 1.1. Общая характеристика имени. Виды имен. 1.2. Отношения между именами. 1.3. Логические операции с именами.
КСР «Логика имен»
Раздел 3. Силлогистика 3.1. Виды и структура атрибутивного высказывания. 3.2. Простой категорический силлогизм (ПКС), его структура и правила анализа. Энтимема.
Раздел 4. Правдоподобные рассуждения 4.1. Виды недедуктивных (правдоподобных) рассуждений 4.2. Ошибки в правдоподобных рассуждениях.
Раздел 5. Логические основы аргументации 5.1. Структура и виды аргументации. 5.2. Правила и ошибки в аргументации.
КСР «Логический анализ языковых выражений» (итоговый тест)
Всего:

СОДЕРЖАНИЕ ДИСЦИПЛИНЫ

ИНФОРМАЦИОННО-МЕТОДИЧЕСКАЯ ЧАСТЬ

ЛИТЕРАТУРА

Основная

1. Берков В.Ф. и др. Логика. - Изд. 7-е. - Мн.: ТетраСистемс, 2008. – 415с.
2. Берков В.Ф. Логика: задачи и упражнения (практикум). - Мн.: ТетраСистемс, 2004. – 221 с.
3. Берков В.Ф. Логика: Элементарный курс. - Мн.: ТетраСистемс, 2009. – 201 с.
4. Брюшинкин В.Н. Логика: Учебник. – Изд. 3-е. - М.: Гардарики, 2001. - 334с.
5. Гетманова А.Д. Логика для юристов. – М.: Омега – Л, 2003. – 418с.
6. Ивлев Ю.В. Логика для юристов. – М.: Дело, 2000. – 261с.
7. Ивлев Ю.В. Логика: Сборник упражнений Учеб.пособие. – Изд. 2-е, перераб. и доп. - М.: Дело, 2002. – 248с.
8. Кириллов В.И. Логика: Учеб.пособие. – М.: Изд. группа «Юристъ», 2002. – 158с.
9. Кузина Е.Б. Логика в кратком изложении и упражнениях: Учеб.пособие. – М.: Изд-во МГУ, 2000. – 240с.
10. Малая Н.В. Тестовые задания и упражнения по логике: Учеб.пособие. Мн.: Изд.центр БГУ, 2004. – 100с.
11. Малыхина Г.И. Логика: Учеб. пособие. - Мн.: Вышэйшая школа, 2005. – 239с.
12. Никифоров А.Л. Логика. – М.: Изд-во «Весь Мир», 2001. – 224с.

Дополнительная

1. Берков В.Ф., Яскевич Я.С. Культура диалога. – Мн.: Новое знание, 2002. – 152с.
2. Гетманова А.Д. Логика: Словарь и задачник: Учеб.пособие для студентов вузов. – М.: Гуманит.изд.цент Владос, 1998. – 336с.
3. Ивин А.А. Практическая логика: Учеб.пособие. М.:ФАИР-ПРЕСС, 2002. – 288с.
4. Кириллов В.И. Упражнения по логике. – М.: ООО «Антэа», 2000. – 159с.
5. Лепешко Б.М. Логические основы правовой практики. - Брест: Изд-во БрГУ, 2003. – 225с.
6. Логический словарь ДЕФОРТ. [Сост. В.Н.Переверзев]. Под ред. А.А.Ивина и др. - М.: Мысль, 1994. – 269с.
7. Поварнин С.И. Искусство спора. – СПб.: Лань, 1996. – 155с.
8. Тер-Акопов А.А. Юридическая логика: Учеб.пособие. – М.: Омега-Л, 2002. – 255с.
9. Яшин Б.Л. Логика. – М.: Элит, 2004. – 416с.

Семинарские занятия (10 ч.)

Высказывания (4 часа).

Вопросы для обсуждения:

1. Высказывания простые и сложные.

2. Логические союзы. Логические операции над высказываниями и их табличное (матричное) определение.

3. Отношения между логическими формами высказываний.

4. Законы логики высказываний.

Литература:

Берков В.Ф. и др. Логика. - Изд. 9-е. - Минск: ТетраСистемс, 2008. – 415с.

Берков В.Ф. Логика: задачи и упражнения (практикум). - Минск: ТетраСистемс, 2002. – 221 с.

Берков В.Ф. Логика: элементарный курс. – Минск: ТетраСистемс, 2007. – 208 с.

Малыхина Г.И. Логика: Учеб. пособие. - Мн.: Вышэйшая школа, 2003. – 239с.

Имена (4 часа).

Вопросы для обсуждения:

1. Структура имени: содержание и объём.

2. Виды имён. Единичные, общие и пустые имена.

3. Отношения между именами: сравнимость и несравнимость, совместимость и несовместимость.

4. Операции обобщение и ограничение (расширение, локализация, типизация).

5. Логическое деление и его структура. Виды логического деления. Правила логического деления и возможные ошибки при их нарушении. Аналитическое деление. Периодизация.

6. Определение (дефиниция) имени и его структура. Виды определений. Правила определения и возможные ошибки при их нарушении.

Литература:

Берков В.Ф. и др. Логика. - Изд. 9-е. - Минск: ТетраСистемс, 2008. – 415с.

Берков В.Ф. Логика: задачи и упражнения (практикум). - Минск: ТетраСистемс, 2002. – 221 с.

Берков В.Ф. Логика: элементарный курс. – Минск: ТетраСистемс, 2007. – 208 с.

Малыхина Г.И. Логика: Учеб. пособие. - Мн.: Вышэйшая школа, 2003. – 239с.

Силлогистические выводы (2 часа).

Вопросы для обсуждения:

1. Атрибутивное высказывание как разновидность простого высказывания и его структура. Виды атрибутивных высказываний по количеству и качеству. Распределённость терминов в атрибутивных высказываниях.

2. Логические отношения между атрибутивными высказываниями: сравнимость и несравнимость, совместимость и несовместимость и их разновидности. Логический квадрат.

3. Простой категорический силлогизм (ПКС) и его структура. Правильные и неправильные силлогизмы. Общие правила силлогизма.

4. Фигуры ПКС и их правила. Понятие модуса фигуры ПКС. Сокращённый категорический силлогизм (энтимема). Процедура восстановления энтимемы до ПКС и проверка её правильности.

Литература:

Берков В.Ф. и др. Логика. - Изд. 9-е. - Минск: ТетраСистемс, 2008. – 415с.

Берков В.Ф. Логика: задачи и упражнения (практикум). - Минск: ТетраСистемс, 2002. – 221 с.

Берков В.Ф. Логика: элементарный курс. – Минск: ТетраСистемс, 2007. – 208 с.

Малыхина Г.И. Логика: Учеб. пособие. - Мн.: Вышэйшая школа, 2003. – 239с.

4.3 Контролируемая самостоятельная работа

СУРС выполняется в форме письменной работы (тестовых заданий) по выше приведенным темам.

Формой контроля за успеваемостью студентов по учебной дисциплине «Логика» является письменное выполнение предложенных тестовых заданий (упражнений). Успешное выполнение заданій служит свидетельством того, что студент освоил теоретический материал, приобрёл навыки его практического применения.

Оценка результатов выполнения контролируемой самостоятельной работы выставляется с учетом количества правильно выполненных заданий соответствующего варианта.

ТИПОВЫЕ ТЕСТОВЫЕ ЗАДАНИЯ

1. Соблюдаются ли элементарные законы логики в рассуждении, если нет, какой закон нарушается? «Свободный доступ к материальным и нематериальным ресурсам означает, что они – ничьи, что они не принадлежат никому или, то же самое, - всем. Такие ресурсы не составляют объекта собственности»?

1) Соблюдены все элементарные законы логики.

2) Нарушен закон тождества.

3) Нарушен закон непротиворечивости.

4) Нарушен закон исключенного третьего.

2. Установите, какие из следующих предложений являются высказываниями?

1) Предложение и спрос идентично взаимодействуют на всех видах рынка.

2) Зрелое яблоко.

3) Осторожно, двери закрываются!

4) Он был свидетелем происшествия и может подробно его описать.

5) Х + У = Z.

6) Кто сегодня дежурный по аудитории?

7) «И какой же русский не любит быстрой езды?» (Н.В.Гоголь)

3. Какой фигуре силлогизма соответствует данное рассуждение: «Все скульпторы – представители искусства, следовательно, некоторые европейцы - представители искусства, так как некоторые скульпторы – европейцы»?

1) I фигуре простого категорического силлогизма;

2) II фигуре простого категорического силлогизма;

3) III фигуре простого категорического силлогизма;

4) это не простой категорический силлогизм;

5) IV фигуре простого категорического силлогизма.

4. Предмет атрибутивного высказывания называется:

1) сущностью;

2) смыслом;

3) силлогизмом;

4) связкой;

5) предикатом;

6) субъектом.

5. Субъект и предикат находятся в отношении пересечения в высказывании (-ях):

1) Среди переводчиков встречаются жители Западной Европы.

2) Некоторые равнобедренные треугольники являются прямоугольными.

3) Большинство млекопитающих не живут в морских глубинах.

4) Некоторые студенты усердно конспектируют первоисточники.

5) Некоторые птицы не являются воробьями.

6. Укажите, в каких случаях произведено аналитическое деление имени:

1) сутки делятся на утро, день, вечер, ночь;

2) газеты делятся на ежедневные, еженедельные, ежемесячные;

3) геометрические фигуры подразделяются на прямоугольные и непрямоугольные;

6) балет состоял из 3 актов;

7) Земной шар делится на Западное и Восточное полушария;

8) учащиеся делятся на успевающих и неуспевающих;

7.Установите вид отношений между парами имён (С – совместимы; Н – несовместимы):

1) физик – скрипач;

2) пароход – судно;

3) известный востоковед - неунывающий рыболов;

4) грек – Аристотель;

5) ливень – град;

6) рыба, которая обитает в некоторых океанах, - рыба, о которой не известно, где она обитает;

7) во всех случаях имена совместимы;

8) нет ни одного случая совместимости имен.

8. Установите, в каких случаях произведена операция обобщения имени правильно.

1) сангвиник, активный человек;

2) М.Булгаков, автор романа «Мастер и Маргарита»;

3) Баренцево море, море, Северный Ледовитый океан;

4) Луна, спутник Земли, спутник;

5) Малая Медведица, созвездие;

6) шкаф, предмет мебели;

7) сосна, растение, тайга;

8) Сатурн, планета, Солнечная система;

9) парус, парусник, парусный флот.

9. Как можно определить вид имени «избирательная система»?

1) Единичное и конкретное.

2) Единичное и абстрактное.

3) Общее и конкретное.

4) Пустое - П и конкретное.

5) Общее и абстрактное.

10. Выберите правильный ответ к задаче и объясните её решение: соотношение объемов имен «1. социальная проблема; 2. преступление; 3. кража; 4. преступность» отражено на схеме.

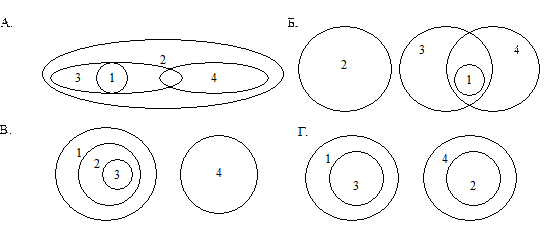
1) А

2) Б

3) В

4) Г

5) ни на одной из схем отношения не отражены

ПРЕДМЕТ ЛОГИКИ КАК НАУКИ

Логика (от греч. logos – слово, понятие, рассуждение, разум) как наука существует около двух с половиной тысяч лет. Её основателем считается великий древнегреческий мыслитель Аристотель (384-322 до н.э.), в настоящее время нет общепринятого определения этой научной дисциплины. Иногда под логикой понимают науку, которая исследует структуры мышления и раскрывает лежащие в его основе закономерности движения к истине. Известно, что мышление как процесс изучают самые различные науки. Так, философия изучает проблему отношения мышления к предметам и явлениям объективного мира. Психология рассматривает специфические закономерности и механизм психической жизни человека. Языкознание интересует сущность слова и знака как инструментов мыслительного процесса человека. Логика же изучает мышление как средство, метод познания действительности. Вот почему в центре логики находятся общечеловеческие законы мыслительного процесса, без соблюдения которых он вообще невозможен. Логика, являясь системой научных знаний, учит человека, как правильно, не нарушая структурно-логической зависимости, применяя ту или иную форму мыслительного анализа, построить стройное рассуждение и, используя формально-логические законы, прийти к истинным выводам в отношении предмета анализа. Соблюдение строгих, научно обоснованных требований логики является непременным условием последовательного, непротиворечивого и обоснованного мышления.

Мы же термин «логика» будем употреблять в более узком значении, рассматривать логику как науку о схемах (логических формах) правильного рассуждения. При этом под рассуждением будем понимать переход от одних мыслей (посылок) к другим (выводам) относительно одного и того же предмета.

В только что принятом определении логики встречаются, неизвестные выражения, которые, естественно, вызывают вопросы: «Что такое схема, или логическая форма, рассуждения (или, в более широком плане, ‑ мысли)?».

Возьмем такие выражения: «Все города являются населенными пунктами»; «Все адвокаты являются юристами»; «Все коммерсанты являются налогоплательщиками». По своему конкретному содержанию мысли, фиксируемые этими выражениями, различны. Тем не менее, эти выражения содержат общие элементы «все», «являются». Чтобы выявить логическую форму, следует отвлечься от содержания рассуждения. В логике принято с этой целью заменять содержательные элементы рассуждения (имена и высказывания) переменными, т.е. знаками, не имеющими никакого содержания и указывающими только на вид заменяемого выражения.

Если отвлечься от содержания каждого предложения, то каждое из них может быть представлено схемой. Для выявления логической схемы (формы) надо отойти от содержания, заменить содержательные части символами. Традиционно для обозначения объектов и их признаков используются соответственно буквы S и Р (начальные буквы латинских слов «субъект» (лат. subjectum – подлежащее) и «предикат» (лат. praedicatum – сказуемое). Тогда получается схема:

Все S являются Р.

Вторая группа выражений: «Если слово стоит в начале предложения, то оно пишется с большой буквы»; «Если А=В, то А²=В²»; «Если в обществе есть классы, то в нем есть государство». От первых предложений они отличаются тем, что являются сложными. Все они образованы с помощью союза «если, то». Отвлекаясь от содержания каждого из приведенных примеров высказываний, введя вместо них соответственно переменные р и q, получим схему:

Если р, то q.

Полученные схемы выражают структурные элементы каждого высказывания. Схемы, или логические формы, которые используются в повседневной языковой практике, весьма разнообразны, их очень много, даже бесконечно много. Обобщенно их суть может быть выражена следующим определением: схема (логическая форма) – это та сторона мысли, которая не зависит от её конкретного содержания, но служит для связи и упорядочения элементов мысли.

В языке логическая форма фиксируется с помощью переменных (в рассмотренных случаях ‑ это S, Р; р, q), а также логических констант. Логическая константа – это выражение, сохраняющее свое значение в любом рассуждении. В качестве логических констант в русском языке выступают слова «все», «некоторые», «есть», «и», «или», «либо, либо», «если, то», «тогда и только тогда, когда», «необходимо», «возможно» и др.

Поскольку логика (в узком смысле) имеет дело с логическими формами, постольку ее называют формальной логикой.

Задача логического исследования – обнаружение и систематизация определенных схем правильного рассуждения. Эти схемы представляют логические законы, лежащие в основе логически правильного мышления. Под ними понимают такие логические формы, которые принимают только истинное значение при любой подстановке вместо переменных конкретных языковых выражений. Рассуждать логично – значит рассуждать в соответствии с законами логики. Их принудительная сила для человеческого мышления объясняется тем, что они являются, в конечном счете, отображением в голове человека наиболее общих отношений реального мира, практики его познания и преобразования человеком. Именно поэтому законы логики кажутся самоочевидными и как бы изначально присущими человеческой способности рассуждать.

Обычно правильность отличают от истинности мышления. Понятие истинности характеризует мышление в его отношении к действительности: уже Аристотель считал, что мысль истинна, если она соответствует действительности. Правильность характеризует мысль с точки зрения внутренней связи между ее элементами. Различие между правильностью и истинностью отчетливо проявляется в тех случаях, когда правильные рассуждения приводят к ложным заключениям. Это возможно лишь тогда, когда исходные данные являются ложными. Так, из ложного положения «Всякая услуга – продукт промышленного производства» с полным правом получается утверждение «Некоторые из продуктов промышленного производства – услуги», которое также является ложным. Познавательные ошибки, связанные с неверными представлениями о действительном положении дел, называются содержательными. Содержательная ошибка может быть результатом заблуждения, или продуктом лжи, дезинформации как целенаправленного действия.

Ошибки, связанные с нарушениями правильности мышления, называются формальными, или логическими. Они делятся на паралогизмы и софизмы.

Паралогизм – это непреднамеренная логическая погрешность. Она, как правило, является продуктом невысокой логической культуры человека. Софизм – преднамеренное нарушение требований логики, прием интеллектуального мошенничества, связанный с попыткой выдать ложь за истину, или наоборот.

Термин «софизм» происходит от древнегреческого sophisma, что означает хитрость. Первоначально софистами в древней Греции называли людей, достигших совершенства в какой-либо области: ремесле, музыке т.д. Затем это слово постепенно приобретает другое значение: им называют философов-профессионалов, учителей мудрости и красноречия, а позже оно приобрело нарицательное значение по отношению к людям, преуспевающим в приемах вводить слушателей в заблуждение.

Логика справедливо рассматривается как основа всех наук, хотя бы по той причине, что в каждой из них употребляются понятия, взятые из области логики, каждое рассуждение должно строиться по законам логики. Традиционно было принято считать, что без знания логики, полученного в практике мышления или путем специального изучения, нет образованного человека. Сейчас, в условиях коренного преобразования характера деятельности людей, ценность такого знания возрастает. Овладение курсом логики – необходимое (хотя и недостаточное) условие повышения не только логической, но и общей культуры каждого высокообразованного специалиста.

ЛОГИЧЕСКАЯ ТЕОРИЯ ВЫСКАЗЫВАНИЙ

1. ОБЩАЯ ХАРАКТЕРИСТИКА ЛОГИКИ ВЫСКАЗЫВАНИЙ

Высказывание - языковое выражение, о котором можно сказать только одно из двух: истинно оно или ложно.

Высказывания (как и соответствующие им схемы построения) делятся на простые и сложные. Сложное высказывание можно разбить на простые. Простое высказывание на более простые не расчленяется.

Алфавит логики высказываний включает символы:

1.p, q, r, s, … – символы, которые обозначают переменные для простых высказываний; A, B, C, D, … - символы, которые обозначают переменные для любых высказываний;

2.Ù, Ú, Ú, ®, «, Ø - символы для обозначения логических союзов;

3.(, ) – скобки как указатели совершения логических действий.

Схема высказывания принимает логическое значение – «истинно» или «ложно».

Логическое значение сложной схемы высказывания в современной логике ставится в зависимость (является функцией) от логических значений простых схем.

Рассмотрим важнейшие схемы логики высказываний.

2. ВИДЫ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ

Сложные высказывания образуются с помощью особых функторов. Важнейшие из них – отрицание, конъюнкция, дизъюнкция (слабая и сильная), импликация, эквиваленция. Cложное высказывание принято называть именем функтора (логического союза), с помощью которого оно образовано.

Отрицанием высказывания А называется высказывание, обозначаемое выражением ØА (читается: «не-А», «неверно, что А»), которое истинно тогда и только тогда, когда А ложно. Данное определение можно выразить с помощью следующей таблицы (таблицы истинности), где «и» обозначает «истинно», а «л» ‑ «ложно»:

А	ØА
и	л
л	и

Конъюнкцией высказываний А и В называется высказывание, обозначаемое выражением А Ù В (читается: А и В), которое истинно тогда и только тогда, когда А и В одновременно истинны. В разговорном языке конъюнкция может быть выражена грамматическими союзами «а», «но», «да», «хотя», «однако» и др. (Государственные пенсии и социальные пособия устанавливаются законом).

Дизъюнкцией слабой высказываний А и В называется высказывание, обозначаемое выражением А Ú В (читается: «А или В»; здесь «или» употребляется в неисключающем смысле), которое истинно тогда и только тогда, когда хотя бы одноиз выражений А и В истинно (Каждый учащийся нашей группы способный илитрудолюбивый).

Дизъюнкцией сильной высказываний А и В называется высказывание, обозначаемое выражением А Ú В (читается: «либо А, либо В»), которое истинно тогда и только тогда, когда лишь одно из выражений А и В истинно (Истец вправе либоувеличивать, либо уменьшать размер исковых требований).

Импликацией высказываний А и В называется высказывание, обозначаемое выражением A ® В (читается: «если А, то В», «из А следует В», «неверно, что А и не-В» и пр.), которое ложно тогда и только тогда, когда А истинно, а В ложно (см. 6-й столбец таблицы). При этом А называется антецедентом (основанием), а В - консеквентом (следствием) импликации (Если прокурор является родственником потерпевшего, то он подлежит отводу).

Эквиваленцией высказываний А и В называется высказывание, обозначаемое выражением А « В (читается: «А эквивалентно В», «А тогда и только тогда, когда В», «А, если и только если В» и пр.), которое истинно тогда и только тогда, когда логические значения А и В совпадают(Страховка выплачивается лишь в том случае, если доказано наличие неумышленного ущерба).

А	В	А Ù В	А Ú В	А Ú В	А ® В	А « В
И	И	И	И	Л	И	И
И	Л	Л	И	И	Л	Л
Л	И	Л	И	И	И	Л
Л	Л	Л	Л	Л	И	И

2. ОТНОШЕНИЯ МЕЖДУ ВЫСКАЗЫВАНИЯМИ И ИХ ЛОГИЧЕСКИМИ ФОРМАМИ

Логические формы простых и сложных высказываний (как и сами высказывания) могут находится в определенных отношениях. Сравнимые логические формы содержат хотя бы одну общую переменную (p, q и т.д. в структуре сложных высказываний), либо одинаковые SиP в структуре простых высказываний.

Несравнимые логические формы не содержат хотя бы одну общую переменную (p, q и т.д. в структуре сложных высказываний), либо состоят из разных SиP в структуре простых высказываний.

Совместимые высказывания и их логические формы содержат хотя бы один случай одновременной истинности (т.е. истинность первой не исключает истинности второй).

2.1. ВИДЫ СОВМЕСТИМОСТИ ВЫСКАЗЫВАНИЙ

Полная совместимость (равнозначность)– отношения между высказываниями, логические значения которых при одинаковых значениях составляющих полностью совпадают.

Частичная совместимость (субконтрарность) – отношения между высказываниями, которые могут быть вместе истинными, но не могут быть вместе ложными.

Следование (подчинение) – отношения между высказываниями, при которых одна логическая форма высказывания является истинной, другая логическая форма также принимает истинное значение (И Þ И).

Несовместимые высказыванияи их логические формы не содержат ни одного случая одновременной истинности (т.е. не могут быть одновременно истинными).

2.2. ВИДЫ НЕСОВМЕСТИМОСТИ ВЫСКАЗЫВАНИЙ

Противоречие (контрадикторность) – отношение между высказываниями и их логическими формами, которые не могут быть вместе истинными, как и не могут быть вместе ложными.

Противность (контрарность) – отношения между высказываниями, которые немогут быть вместе истинными, но могут быть одновременно ложными.

3. АНАЛИЗ ПРАВИЛЬНОСТИ РАССУЖДЕНИЙ В ЛОГИКЕ ВЫСКАЗЫВАНИЙ

Законы логики высказываний. Специфика законов логики высказываний в том, что в качестве значений переменных, входящих в структуру логических форм, выступают отдельные простые высказывания как целостные образования. И какие бы высказывания ни подставлялись вместо переменных в логический закон, результат будет одним и тем же ‑ полученное сложное высказывание будет истинным.

Правильные схемы рассуждений (= логический закон) - логические схемы, которые при любых подстановках преобразуются только в истинные выражения.

Выполнимые схемы рассуждений - логические схемы, которые при одних подстановках конкретных высказываний преобразуются в истинные, а при других в ложные выражения.

Противоречивые (невыполнимая) схемы рассуждений -логические схемы, которые при любых подстановках преобразуются исключительно в ложные выражения.

Наиболее простыми законами логики высказываний являются законы, которые можно выразить с помощью одной переменной – закон исключенного третьего, закон противоречия, закон тождества, закон удаления двойного отрицания, введения двойного отрицания и др.

Закон исключенного третьего– схема AÚØA – два отрицающих друг друга высказывания не являются вместе ложными, выполняется одна из возможностей: если ложно одно из этих высказываний, то истинно его отрицание, а что-либо третье исключено.

Закон противоречия - схема Ø(AÙ ØA) - два отрицающих друг друга высказывания не являются вместе истинными, одно их них ложно.

Закон тождества – схема A«A – всякое высказывание является эквивалентным (тождественным) самому себе, следовательно, в правильном рассуждении оно согласуется с самим собой.

ЛОГИЧЕСКАЯ ТЕОРИЯ ИМЕН

1. ОБЩАЯ ХАРАКТЕРИСТИКА ИМЕНИ

Имя ‑ выражение языка, обозначающее предмет или множество, совокупность предметов. При этом «предмет» понимается в самом широком, обобщенном смысле слова. Предметы, мысленно объединяемые в некоторое множество или класс, называются элементами множества (класса).

Множество (совокупность, класс) предметов, обозначаемых именем, называется объемомимени. Например, слово «Цезарь» обозначает отдельный предмет – первого римского императора Цезаря; слово «ученый» обозначает класс людей, каждый из которых занят научными исследованиями; слово «черный» может рассматриваться как обозначение свойства черноты; слово «независимость» – как обозначение определенного отношения между предметами и т.п.

Содержаниеимени‑ совокупность мыслимых в имени признаков предметов. Под признаком понимается любое свойство, любая характеристика предмета. Содержание имени должно фиксировать, выражать какие-то свойства, признаки, характеристики обозначаемых именем предметов, которые были бы в своей совокупности присущи каждому предмету, выделяемому этим именем (т.е. входящему в объем этого имени), и только этим предметам.

2.1. ВИДЫ ИМЕН ПО ОБЪЕМУ

Одним из важных аспектов в различии имен является количество объектов, составляющих объем имени. В этом плане различают единичные, общие и нулевые (или как их иногда называют, пустые) имена.

Если в объем имени входит только один предмет, то такое имя называют единичным. Каждое из единичных имен однозначно выделяет единственное именуемое им лицо или событие и др. («Декларация прав человека», «самое глубокое озеро в мире»).

Общееимя‑ это имя, в объем которого входит более одного элемента. Объемы общих имен ‑ соответствующие множества (классы) охватываемых ими предметов («ценная бумага», «директор предприятия», «источник права»). Класс, являющийся объемом общего имени, называют значением этого имени.

Нулевые (пустые) имена в самом общем виде определяются как имена, объем которых не содержит ни одного элемента. Класс, не содержащий ни одного элемента, называют нулевым, или пустым («металл-диэлектрик», «четвертый Статут ВКЛ», «столица Беларуси, расположенная на реке Дунай», «областной центр Беларуси с населением менее 100 тыс. чел»).

2.2. ВИДЫ ИМЕН ПО СОДЕРЖАНИЮ

Важно различать собирательные и несобирательные имена. Несобирательным называется такое имя, каждый элемент объема которого представляет собой нечто единое, целостное («лауреат музыкального конкурса», «государственное предприятие», «звезда»). Собирательнымназывается такое имя, каждый элемент которого является совокупностью, собранием, объединением каких-то объектов («березовая роща», «стая птиц», «созвездие Северного полушария»). В несобирательных именах абстрагируются от того обстоятельства, что входящие в их объем объекты тоже состоят их каких-то элементов, некоторым образом между собой структурированных. В собирательных же именах это обстоятельство, напротив, является одним из важнейших аспектов их содержания.

Нельзя путать общность или единичность имен с собирательностью или несобирательностью. И несобирательные, и собирательные имена бывают как единичные, так и общие.

Относительные имена называют предметы, связанные отношением с какими-либо другими предметами (признаки-отношения) (кредитор, ответчик, верх, причина). Безотносительные имена называют предметы, признаки которых не содержат указаний на какие-либо отношения (игрок, островное государство).

Положительные – имена, содержание которых составляют признаки, присущие предмету (водоплавающая птица, законная сделка). Отрицательные – имена, содержание которых указывает на отсутствие у предмета определенных свойств (неграмотность, необитаемый остров).

Конкретныеимена – имена, обозначающие существующие предметы (нормативно-правовой акт, косвенный налог). Абстрактныеимена – признак предмета или отношение между предметами (ответственность, увлеченность, тождественность, гениальность Л.да Винчи).

Укажем деление имен на четкие и нечеткие. Если имя таково, что относительно любого предмета можно точно, однозначно решить, входит или не входит этот предмет в объем данного имени, то это имя называют четким(точным, определенным) по объему (государственный обвинитель, туристический объект). В противном случае, имя считается нечетким(неопределенным, расплывчатым) по объему (дорогая вещь, молодой писатель).

3. ОТНОШЕНИЯ МЕЖДУ ИМЕНАМИ

В зависимости от специфики отношений между содержаниями и объемами имен выделяется несколько видов отношений между ними.

Имена являются сравнимыми между собой, если их содержания имеют общие признаки. Если же в содержании имен нет общих признаков, позволяющих выделить основания для сравнения, то имена являются несравнимыми. Примеры «право» и «мораль» содержат общий признак – «общественное явление». Не содержат общих признаков объемы предметов «право» и «всемирное тяготение», поэтому они будут несравнимыми.

Сравнимые имена делятся на совместимые и несовместимые. Имена считаются совместимыми если их объемы хотя бы частично совпадают, т.е. эти объемы имеют общие элементы. В противном случае имена несовместимы.

Имеется три вида отношений совместимости: 1) отношение равнообъемности (равнозначности), 2) отношение подчинения, 3) отношение пересечения (перекрещивания).

Равнообъемными (равнозначными) считаются имена, объемы которых полностью совпадают (рис. 1). Схема читается следующим образом: «(Любой элемент класса) А является В и наоборот, В (любой элемент множества) является элементом А» (столица Беларуси – самый крупный населенный центр Республики Беларусь).

Имена находятся в отношении подчинения, если объем одного полностью включается в объем другого, но не совпадает с ним. При этом включающее имя называется подчиняющим, а включенное – подчиненным (рис. 2). Схема ч