Декартово произведение множеств
Декартово, или прямое, произведение множеств введено в 1637г. французским математиком Р. Декартом (1596–1650 гг.).
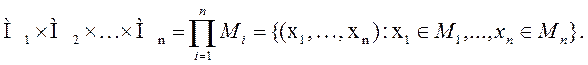 Элементами этого произведения–множества являютсянаборы, или кортежи. Набор длины n – это последовательность n элементов, например (x1, x2, …, xn). Здесь, в отличие от множества, порядокважен.
Элементами этого произведения–множества являютсянаборы, или кортежи. Набор длины n – это последовательность n элементов, например (x1, x2, …, xn). Здесь, в отличие от множества, порядокважен.
Итак,
Если все множества одинаковы, получается декартова степень:
М 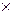 М
М 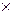 …
… 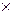 М = Мn.
М = Мn.
 |
n
Декартово произведение некоммутативно: X 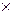 Y ¹ Y
Y ¹ Y 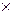 X.
X.
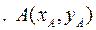

 Примеры:
Примеры:
R
 | |||
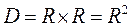 | |||
R
шахматная доска: W={a,b,…,h}, G={1,2,…,8}, D = W×G = {(a,1)…(h,8)}, |D|=64
Декартовым (прямым) произведением A ´ B множеств A и B является множество всех упорядоченных пар (x, y), где x Î X и y Î Y:
A ´ B=í(x, y): xÎA & yÎBý.
Пример: А={-1;0;2}, В={3;6}
Ах В={(-1;3), (-1;6), (0;3), (0;6), (2;3), (2;6)}.
Пример: А=[-1;4), В=R
 |
Нарисовать декартово произведение окружности с отрезком, длиной [0,1]
Свойства декартова произведения
1° АхВ¹ВхА
2° Если у нас имеются 3 непустых множества А, В, С и множество АÍВ, тогда декартово произведение АхСÍВхС
3° Если даны любые три непустые множества А, В, С и АхВÍВхСÞ АÍС
4° Пусть нам даны любые три непустые множества А, В, С, тогда
Ах(В  С)=(АхВ)
С)=(АхВ)  (АхС)
(АхС)
G F
При доказательстве будем использовать антисимметричность отношения включения.
Доказательство разобьется на 2 этапа:
1) GÍF
Þ F=G
2) FÍG
1. Покажем, что GÍF, для этого зафиксируем пару (х,у)ÎG или (х,у)ÎАх(В 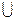 С)
С)
хÎА и уÎ(В 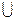 С) Þ хÎА и уÎВ или уÎС Þ (х,у)Î АхВ или (х,у)Î АхС Þ
С) Þ хÎА и уÎВ или уÎС Þ (х,у)Î АхВ или (х,у)Î АхС Þ
Þ (х,у)Î(АхВ) 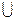 (АхС) Þ GÍF
(АхС) Þ GÍF
2. Покажем, что FÍG (доказать самостоятельно)
Из (1) и (2) Þ G=F
Утверждение: Пусть nÎN. Множество А1, А2,…, Аn непустые. Пусть множество Аi – конечное, тогда |А1хА2х…хАn|=|А1|×|А2|×…×|Аn| (*)
Для доказательства будем использовать метод математической индукции. База индукции: n=2. Рассмотрим два множества с мощностями |А1|=n и |А2|=m.
1) Пусть А1={а1, а2,…, аn}, множество А2={ b1,b2,…, bm}. Выполним декартово произведение множеств.
А1х А2={(а1,b1), (а1,b2),…,(а1,bm),(а2,b1), (а2,b2),…,(а2,bm),…,(аn,b1), (аn,b2),…,(аn,bm)}
|А1хА2|=nхm=|А1|×|А2|.
2) Предположим, что наша функция (*) верна для всех k=n-1, т.е.
|А1хА2х…хАn-1|=|А1|× |А2|×…×|Аn-1| (**)
3) Осуществляем индукционный переход, рассмотрим мощность декартова произведения n множеств, по пункту (1).
Можно записать |А1хА2х…хАn|=|А1|×|В|, где В=А2х…хАn, т.е. формула (**) может быть использована
|А1хА2х…хАn|=|А1|×|В|=|А1|×|А2|×…×|Аn|
Из (1-3) следует, что наша формула (*) верна для всех nÎN/{1}.
Элементы комбинаторики
Принцип сложения
Если выбор А можно осуществить n способами, а выбор В можно осуществить m способами, то выбор либо А, либо В можно осуществить m+n способами, в случае если при выборе способов нет совпадений, если k – число совпадений, то выбор либо А либо В можно осуществить m+n-k способами.
Принцип умножения
Пусть выбор А можно осуществить n способами, а выбор В - m способами, тогда выбор А и В можно осуществить m*n способами.
Решим задачу.
1.Из Ростова-на-Дону до Москвы можно добраться пароходом, поездом, автобусом и самолетом. Из Москвы до Санкт-Петербурга поездом, автобусом и самолетом. Сколькими способами можно осуществить путь по маршруту Ростова-на-Дону – Москва - Санкт-Петербург.
| Ростова-на-Дону | пароходом | Москва | поездом | Санкт-Петербург |
| поездом | автобусом | |||
| автобусом | самолетом | |||
| самолетом |
4*3=12
Выбор А*В можно осуществить 12 способами.
2.В стране чудес есть 4 города А, В, С, Д. Из города А в город В ведет 6 дорог, из В в Д – 4, из А в С – 2, из С в Д – 3. Сколькими способами можно проехать от А до Д.
| А | В | |
| С | Д |
2*3+6*4=30
Соединения без повторений
| Соединение предметов | ||
 | 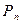 | 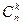 |
| Размещение из n элементов по k элементам (важен порядок и важны сами элементы) | Перестановка n элементов без повторения (важен порядок, элементы не важны) | Сочетание из n элементов по k элементам (важны элементы, порядок не важен) |
Определение: Введем множество N0=NÈ{0}.Пусть элементы k, n ÎN0, причем k£n. Размещением из n элементов множества В={b1, b2,…, bn} по k элементам будем называть всякую последовательность, составленную из неповторяющихся элементов множества В, имеющую длину k
(а1, а2, …, аk).
Пример: А={1,2,3}. Выпишем все размещения из трех элементов по 2
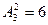 (1,2); (1,3); (2,1); (2,3); (3,1); (3,2)
(1,2); (1,3); (2,1); (2,3); (3,1); (3,2)
ТеоремаПусть дано множество В={b1, b2,…, bn} k, n ÎN0, k£n. Число размещений из n элементов по k элементам без повторений можно вычислить по формуле:
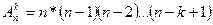 =
= 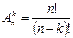
Для доказательства воспользуемся принципом умножения. Для построения каждого размещения нужно рассмотреть последовательность из n элементов. На первом месте n возможностей, на втором n-1.
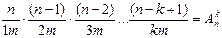
Пусть (n-k)!=1*2*3*…(n-k) n!=1*2*3*…*(n-k)*(n- k +1)*…*n
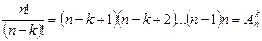
Определение: Пусть N0=NÈ{0}, k, n ÎN0, k£n, В={b1, b2,…, bn}. Сочетаниемиз n элементов по k элементам без повторений будем называть всякое подмножество множества В, состоящее из k неповторяющихся элементов заданного множества В.
Пример: А={0,1,4}. Выпишем все размещения из трех элементов по 2
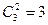 {0,1}; {1,4};{ 0,4}
{0,1}; {1,4};{ 0,4}
ТеоремаПусть k, n ÎN0, k£n, В={b1, b2,…, bn}. Число сочетаний из n элементов по k элементам можно подсчитать используя формулу: 
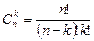
Рассмотрим формулу из предыдущей теоремы. Число размещений равно 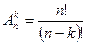 . Ясно, что число размещений
. Ясно, что число размещений 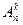 можно связать с числом сочетаний формулой
можно связать с числом сочетаний формулой 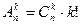 .
. 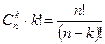 следовательно
следовательно 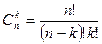 .
.
Задача: Сколькими способами можно рассадить 4 учащихся на 25 местах.
I способ (принцип умножения)
25*24*23*22=303600
II способ (размещение)
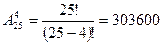
Задача: Учащемуся необходимо сдать 4 экзамена на протяжении 8 дней. Сколько способов? Решить задачу если известно, что последний экзамен будет сдаваться на 8 день.
1) 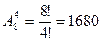
2) 4* 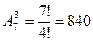
Задача: Сколькими способами читатель может выбрать 3 книги из 5.
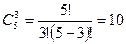
Задача: В турнире принимали участие n шахматистов, каждые два шахматиста встретились 1 раз. Сколько партий было в турнире?
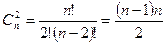
Определение: Пусть n ÎN0, В={b1, b2,…, bn}. Перестановкой n элементов множества В будем называть всякое размещение без повторений из n элементов по n элементам.
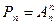
Теорема 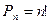 . Число перестановок n элементов множества равно n! n ÎN0, В={b1, b2,…, bn}.
. Число перестановок n элементов множества равно n! n ÎN0, В={b1, b2,…, bn}.
Пусть 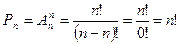
Следствие: n, k ÎN0, k£n, В={b1, b2,…, bn}. Число размещений из n элементов по k элементам модно вычислить по формуле:
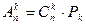
Задача: Сколькими способами можно разместить в очередь 7 человек.
N=7 Р7=7!
Задача: Сколькими способами можно упорядочить множество 1, 2, 3, …, 2n, так чтобы каждое четное число имело четный номер.
А={1, 2, 3, …, 2n} n!*n!=(n!)2.
Задача: Сколько можно составить перестановок из n элементов, в которых данные два элемента не стоят рядом.
n!-(n-1)!2!=(n-1)!(n-2)
Свойства сочетаний
1° 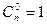 2°
2° 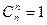 3°
3° 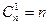
4° 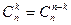 5°
5° 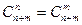 6°
6° 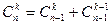 7°
7° 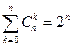 ( из7)
( из7)
Из св 6 можно последовательно находить 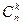 зная
зная 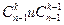 . в виде треугольника Паскаля:
. в виде треугольника Паскаля:
Формула бинома Ньютона
(а+b)n= 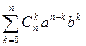 (можно доказать по индукции)
(можно доказать по индукции)
Перемножим (а+b) само на себя n раз, получим сумму, содержащую 2n слагаемых, каждое слагаемое представляет произведение d1*d2*…*dn, где di либо а, либо b, 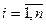 , полученную сумму разобьем на n+1 слагаемых В0, В1, …Вn.
, полученную сумму разобьем на n+1 слагаемых В0, В1, …Вn.
Пусть у нас в группе Вk содержатся те произведения, в которых элемент b встречается k раз, а элемент a встречается (n-k) раз.
