Полным или закрытым называют дизъюнктивное суждение, в котором перечислены все признаки или все виды определенного рода.

Символически это суждение можно записать следующим образом:

<р v q v r>.

Например: «Леса бывают лиственные, хвойные или смешанные». Полнота этого разделения (в символической записи обозначается знаком <...>) определяется тем, что не существует, помимо указанных, других видов лесов.

Неполным или открытым называют дизъюнктивное суждение, в котором перечислены не все признаки или не все виды определен­ного рода. В символической записи неполнота дизъюнкции может быть выражена многоточием:

р v q v r v...

В естественном языке не­полнота дизъюнкции выражается словами: «и т.д.», «и др.», «и тому подобное», «иные» и другими.

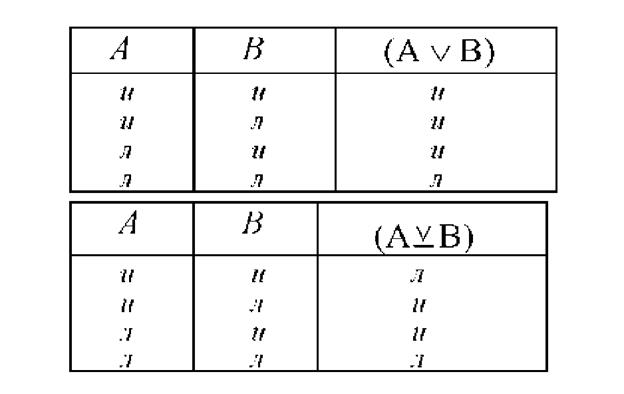
Условные суждения .Таблица истинности для импликации.

Условные (импликативные) суждения — состоят из нескольких простых, связанных логической связкой «если..., то...» (р→q), где р — антецедент (предшествующий) выполняет функцию фактического или логического основания, q — консеквент (последующий). Если предохранитель плавится (р), то электролампа гаснет (q) (там..., где; тогда..., когда...; постольку..., поскольку; при наличии..., следует...; в случае..., следует...; при условии..., наступает...).

Условие истинности импликации — импликация истинна во всех случаях, кроме одного: при истинности антецедента (р — если...) и ложности консеквентна (q — то...) импликация будет ложной.

Зависимость между антецедентом-основанием и консеквентом-следствием характеризуется свойством достаточности — истинность основания обуславливает истинность следствия (при истинности основания, следствие всегда будет истинным). При этом основание не характеризуется свойством необходимости для следствия, ибо при ложности основания, следствие может быть как истинным, так и ложным.

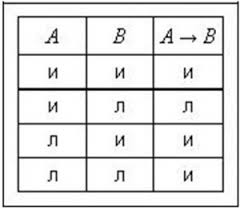
Эквивалентные суждения. Таблица истинности для двойной имплиекации.

Эквивалентным называют суждение, включающее в качестве составных два суждения, связанных двойной (прямой и обратной) условной зависимостью, выражаемой логической связкой «если и только если ..., то ...».

Например: «Если и только если человек награжден орденами и медалями (а), то он имеет право на ношение соответствующих орденских планок (в)».

Логическая характеристика этого суждения состоит в том, что истинность утверждения о награждении (а) рассматривается как необходимое и достаточное условие истинности утверждения о наличии права на ношение орденских планок (в). Точно так же истинность утверждения о наличии права на ношение орденских планок (в) является необходимым и достаточным условием истинности утверждения о том, что данное лицо награждено соответствующими орденом или медалью (а).

Используется союз если и только если…, то… (тогда и только тогда, когда…).

Например: «Если студент сдал все зачеты и экзамены, то может быть переведен на следующий курс».

Эквиваленция обозначается знаком «↔».

Схема: «а ↔ в». Читается: «если, и только если А, то В».

В естественном языке, в том числе и в юридических текстах, для выражения эквивалентных суждений используют союзы: «лишь при условии что..., то...», «в том и только в том случае когда..., тогда...», «только тогда когда..., то...» и другие.

Суждение «а»	Суждение «в»	«а ↔ в»
истинно	истинно	истинно
истинно	ложно	ложно
ложно	истинно	ложно
ложно	ложно	истинно

Закон тождества

Сущность закона: каждая мысль или понятие о предмете должны быть четкими и сохранять свою однозначность на протяжении всего рассуждения и вывода.

Нарушением этого закона является подмена понятий (часто используется в адвокатской практике).

В этом законе непосредственно проявляется природа самых фундаментальных свойств логической мысли — определенности и последовательности.

Иначе этот закон можно выразить так: мысли о предметах, свойствах или отношениях должны оставаться неизменными по содержанию в процессе всего рассуждения о них.

Причиной возникновения ошибок чаще всего является многозначность слов и, как следствие, нарушение закона тождества при рассуждении. Как, скажем, понимать такое предложение: «Партия фортепиано доставила большой коммерческий успех»? Идет ли здесь речь о блестящем исполнении и большом сборе благодаря нему или имеются в виду проданные за хорошую цену музыкальные инструменты?

Неоднозначность выражений может возникать и из-за двусмысленных грамматических конструкций. Путаница, вызванная такого рода обстоятельствами, знакома каждому благодаря знаменитому «казнить нельзя помиловать». «Беспечность порождает самонадеянность». В нем нельзя понять, что имеется в виду под порождаемым, а что под порождающим. Совершенно аналогичны в этом отношении выражения вроде: «Взвод сменяет караул» или «Меньшинство подчиняет большинство». Остроумно использовал двусмысленность выражения А.П. Чехов, вложив в уста одного из персонажей сообщение: «Перед вами череп обезьяны очень редкой разновидности. Таких черепов у нас всего два, один — в Национальном музее, другой — у меня».

Нельзя отождествлять различные мысли, нельзя тождественные мысли принимать за нетождественные. Результат применения — закон тождества обеспечивает определенность логического мышления.

Закон непротиворечия.

Закон непротиворечия (lex contradictionis) указывает на недопустимость одновременного утверждения (в рассуждении, в тексте или теории) двух суждений, из которых одно является логическим отрицанием другого, то есть суждений вида A и A или их конъюнкции, или эквиваленции, или — в более широком смысле — утверждений о тождестве заведомо различных объектов, поскольку обычно правила логики таковы, что позволяют из противоречия выводить произвольные суждения, что обесценивает содержательный смысл умозаключений или теорий. Наличие противоречия в рассуждении (теории) создаёт парадоксальную ситуацию и нередко указывает на несовместимость посылок, положенных в основу рассуждения (теории). Этим обстоятельством часто пользуются в косвенных доказательствах.

Закон исключнного третьего.

Закон исключённого третьего (lex exclusii tertii) на логическом языке записывается формулой A ⌵ A и утверждает, что нет ничего среднего (промежуточной оценки) между членами противоречивой пары (отсюда другое латинское название этого закона — tertium non datur). В методологическом плане этот закон выражает конструктивно неоправданную идею о разрешимости (потенциально осуществимом указании на истинность или ложность) произвольного суждения. В отличие от формулы, соответствующей закону противоречия, формула, соответствующая закону исключённого третьего, не выводима в интуиционистских и конструктивных исчислениях, хотя и неопровержима в них. Дихотомия установленных истины и лжи неоспорима, но дихотомия утверждения и отрицания оспаривалась неоднократно. Наиболее последовательную критику закона исключённого третьего дал Л. Э. Я. Брауэр. В свете его критики этот закон следует рассматривать только как принцип (или постулат) классической логики.