Суждение, как форма мышления

Суждение, как форма мышления

Более сложной по сравнению с понятием формой мышления выступает суждение. Оно включает понятие, но не сводится к нему, а представляет собой качественно особую форму, выполняющую иные свои функции в мышлении. В нем утверждается или отрицается связь между предметом и его признаком или отношение между предметами. Суждение обладает свойством выражать либо истину, либо ложь.

Истинное суждение – суждение в котором мысль, отражая действительность, во-первых, связывает то, что связано в самой действительности; во-вторых, в истинном суждении мысль связывает предметы и разделяет их таким образом, каким они связываются и разделяются в самой действительности.

Ложное суждение – суждение в котором мысль, во-первых, связывает то, что не связано в самой действительности, и разделяет то, что в самой действительности СО связано, во-вторых, суждение ложно даже в тех случаях, когда оно, пытаясь соединить то, что соединено в самой действительности, связывает предметы не так, как они связаны в самой действительности.

Каждое суждение обладает определенной структурой, состоящей из двух тесно связанных между собой компонентов: субъекта и предиката.

Субъект суждения – это понятие, о котором что-либо утверждается или отрицается, сокращенно обозначается в логике буквой «S».

Предикат суждения – это понятие о том, что именно утверждается или отрицается о некотором другом понятии, сокращенно обозначается буквой «Р».

Субъект и предикат называются терминами суждения. В этом состоит одна из логических функций понятий.

Термины суждения носят соотносительный характер. Один не существует без другого. Однако роль

терминов в суждении далеко не одинакова. Субъект содержит уже известное знание, а предикат несет о нем новое знание.

Отношение между субъектом и предикатом раскрывается посредством логической связки и в языке выражается словами «есть» («не есть»), «является» («не является»), «представляет собой» («не представляет собой») и др. Иногда связка отсутствует, а логическое соотношение между субъектом и предикатом раскрывается посредством грамматического согласования слов: «Конституция принята».

Материальной формой суждения, ее носителем является предложение. Повествовательные предложения выражают суждение. В вопросительных предложениях суждения содержатся неявно. Побудительные предложения, подобно вопросительным, также основаны на каких-либо суждениях. В полном смысле суждения выражают только повествовательные предложения.

Обладая определенной структурой, суждения различаются прежде всего по степени сложности. В зависимости от этого суждения делятся на две большие группы – простые и сложные.

Простые суждения – это суждения, в которых нельзя выделить правильную часть, которая в свою очередь была бы самостоятельным суждением. Например: «Я – человек» или «Ничто человеческое мне не чуждо».

Сложные суждения состоят из двух или более простых суждений, они выражаются при помощи сложных предложений или предложений с однородными членами. Например: «Я – человек, и ничто человеческое мне не чуждо».

Простые суждения и их виды

Поскольку в простых суждениях выражается безусловная связь между компонентами мысли, то их еще называют категорическими.

Особое значение в логике придается делению простых суждений на виды по характеру связки (ее качеству) и субъекта (по его количеству).

Качество суждения выражает не фактическое содержание, а логическую форму: утвердительную или отрицательную.

По характеру связки простые суждения делятся на утвердительные и отрицательные.

В утвердительных суждениях раскрывается наличие какой-либо связи между субъектом и предикатом: «S есть Р».

В отрицательных суждениях раскрывается отсутствие той или иной связи между субъектом и предикатом: «S не есть Р».

Также простые суждения делятся по количеству.

Количество суждения определяется логическим объемом суждения. В зависимости от этого выделяются общие, частные и единичные суждения.

Общими называются суждения, в которых что-либо утверждается для всей группы предметов в раздельном смысле: «Все S есть Р» («Ни одно S не есть Р»).

Частные суждения – это суждения, в которых что-либо высказывается о части какой-то группы предметов:

«Некоторые S есть (не есть) Р».

Единичные суждения – это такие суждения, в которых нечто высказывается об отдельном предмете мысли: «Это S есть (не есть) Р».

В логике большое значение придается объединенной классификации суждений по их количеству и качеству. Выделяют четыре вида таких суждений: общеутвердительные, частноутвердительные, общеотрицательные, частноотрицательные.

Общеутвердительными являются суждения, которые по количеству общие, а по качеству – утвердительные. Например: «Все адвокаты – юристы».

Частноутвердительные суждения – частные по количеству, утвердительные по качеству. Например: «Некоторые свидетели дают достоверные показания».

Общеотрицательные – общие по количеству, отрицательные по качеству. Например: «Ни один обвиняемый не оправдан».

Частноотрицательные – частные по количеству, отрицательные по качеству. Например: «Некоторые свидетели не дают верных показаний».

Предикат суждения, будучи носителем новизны, может иметь различный характер. С этой точки зрения выделяют: атрибутивные, реляционные и экзистенциальные.

Атрибутивные суждения – раскрывают наличие или отсутствие у предмета мысли тех или иных свойств или признаков: «СНГ непрочен».

Реляционные суждения – раскрывают наличие или отсутствие у предмета мысли того или иного отношения к другому предмету: «СНГ не равно СССР».

Экзистенциальные суждения – раскрывают наличие или отсутствие предмета мысли: «СНГ существует».

Отношения между простыми суждениями определяются, с одной стороны, их конкретным содержанием, а с другой – логической формой. По содержанию простые суждения бывают сравнимые и несравнимые.

У несравнимых суждений предметные области совершенно не совпадают.

Сравнимые суждения имеют одинаковые термины, но могут различаться по количеству и качеству.

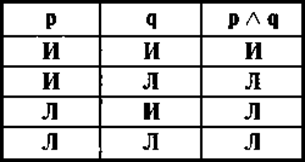
Соединительные суждения. Таблица истинности для конъюнкции.

Соединительные (конъюнктивные) суждения — состоят из нескольких простых, связанных логической связкой «и» (р٨q), где p,q — конъюнкты: Кража и мошенничество относятся к умышленным преступлениям (а, но, а также, как и, одновременно). Может быть многосоставным: р٨q٨r٨...٨n.

Соединительное суждение может быть выражено одной из трех логико-грамматических структур:

1.Соединительная связка представлена в сложном субъекте — S1 и S2 есть P — Конфискация имущества и лишения звания являются дополнительными уголовно-правовыми санкциями;

2.Соединительная связка представлена в сложном предикате — S есть Р1 и Р2 — Преступление — это общественно опасное и противоправное деяние;

3.Соединительная связка представлена в сложном предикате и сложном субъекте — S1 и S2 есть Р1 и Р2 — «С полицмейстером и прокурором Ноздрев тоже был на «ты» и общался по-дружески» (Н.В. Гоголь).

Соединительное суждение истинно при истинности всех составляющих его конъюнктов и ложно при ложности хотя бы одного из них.

Разделительные суждения. Полная и неполная, строгая и слабая дизъюнкция. Таблица истинности для дизъюнкции.

азделительным, или дизъюнктивным, называют суждение, со­стоящее из нескольких простых, связанных логической связкой «или».

Разделительное суждение может быть как двух-, так и многосо­ставным: р Ú q Ú r Ú… n

В языке разделительное суждение может быть выражено одной из трех логико-грамматических структур.

1) Разделительная связка представлена в сложном субъекте по схеме: S₁ или S₂ есть Р.

2) Разделительная связка представлена в сложном предикате по схеме: S есть P₁ или P₂.

3) Разделительная связка представлена сочетанием первых двух способов по схеме: S₁ или S₂есть P₁ или P₂.

Нестрогая и строгая дизъюнкция. Поскольку связка «или» упот­ребляется в естественном языке в двух значениях — соединительно-разделительном и исключающе-разделительном, то следует разли­чать два типа разделительных суждений: 1) нестрогую (слабую) ди­зъюнкцию и 2) строгую (сильную) дизъюнкцию.

1) Нестрогая дизъюнкция — суждение, в котором связка «или» употребляется в соединительно-разделительном значении (сим­вол v).

2) Строгая дизъюнкция — суж­дение, в котором связка «или» упот­ребляется в разделительном значе­нии (символ ).

Члены строгой дизъюнкции, называемые альтернативами, не могут быть одновременно истинными.

Разделительная связка в языке обычно выражается с помощью союзов «или», «либо». С целью усиления дизъюнкции до альтерна­тивного значения нередко употребляют удвоенные союзы: вместо выражения «р или q» употребляют «или р, или q», а вместе «р либо q» — «либо р, либо q». Поскольку в грамматике отсутствуют одно­значные союзы для нестрогого и строгого разделения, то вопрос о типе дизъюнкции в юридических и других текстах должен решаться содержательным анализом соответствующих суждений.

Полная и неполная дизъюнкция.Среди дизъюнктивных сужде­ний следует различать полную и неполную дизъюнкцию.

Условные суждения .Таблица истинности для импликации.

Условные (импликативные) суждения — состоят из нескольких простых, связанных логической связкой «если..., то...» (р→q), где р — антецедент (предшествующий) выполняет функцию фактического или логического основания, q — консеквент (последующий). Если предохранитель плавится (р), то электролампа гаснет (q) (там..., где; тогда..., когда...; постольку..., поскольку; при наличии..., следует...; в случае..., следует...; при условии..., наступает...).

Условие истинности импликации — импликация истинна во всех случаях, кроме одного: при истинности антецедента (р — если...) и ложности консеквентна (q — то...) импликация будет ложной.

Зависимость между антецедентом-основанием и консеквентом-следствием характеризуется свойством достаточности — истинность основания обуславливает истинность следствия (при истинности основания, следствие всегда будет истинным). При этом основание не характеризуется свойством необходимости для следствия, ибо при ложности основания, следствие может быть как истинным, так и ложным.

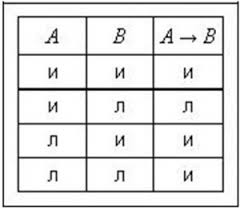
Эквивалентные суждения. Таблица истинности для двойной имплиекации.

Эквивалентным называют суждение, включающее в качестве составных два суждения, связанных двойной (прямой и обратной) условной зависимостью, выражаемой логической связкой «если и только если ..., то ...».

Например: «Если и только если человек награжден орденами и медалями (а), то он имеет право на ношение соответствующих орденских планок (в)».

Логическая характеристика этого суждения состоит в том, что истинность утверждения о награждении (а) рассматривается как необходимое и достаточное условие истинности утверждения о наличии права на ношение орденских планок (в). Точно так же истинность утверждения о наличии права на ношение орденских планок (в) является необходимым и достаточным условием истинности утверждения о том, что данное лицо награждено соответствующими орденом или медалью (а).

Используется союз если и только если…, то… (тогда и только тогда, когда…).

Например: «Если студент сдал все зачеты и экзамены, то может быть переведен на следующий курс».

Эквиваленция обозначается знаком «↔».

Схема: «а ↔ в». Читается: «если, и только если А, то В».

В естественном языке, в том числе и в юридических текстах, для выражения эквивалентных суждений используют союзы: «лишь при условии что..., то...», «в том и только в том случае когда..., тогда...», «только тогда когда..., то...» и другие.

Суждение «а»	Суждение «в»	«а ↔ в»
истинно	истинно	истинно
истинно	ложно	ложно
ложно	истинно	ложно
ложно	ложно	истинно

Закон тождества

Сущность закона: каждая мысль или понятие о предмете должны быть четкими и сохранять свою однозначность на протяжении всего рассуждения и вывода.

Нарушением этого закона является подмена понятий (часто используется в адвокатской практике).

В этом законе непосредственно проявляется природа самых фундаментальных свойств логической мысли — определенности и последовательности.

Иначе этот закон можно выразить так: мысли о предметах, свойствах или отношениях должны оставаться неизменными по содержанию в процессе всего рассуждения о них.

Причиной возникновения ошибок чаще всего является многозначность слов и, как следствие, нарушение закона тождества при рассуждении. Как, скажем, понимать такое предложение: «Партия фортепиано доставила большой коммерческий успех»? Идет ли здесь речь о блестящем исполнении и большом сборе благодаря нему или имеются в виду проданные за хорошую цену музыкальные инструменты?

Неоднозначность выражений может возникать и из-за двусмысленных грамматических конструкций. Путаница, вызванная такого рода обстоятельствами, знакома каждому благодаря знаменитому «казнить нельзя помиловать». «Беспечность порождает самонадеянность». В нем нельзя понять, что имеется в виду под порождаемым, а что под порождающим. Совершенно аналогичны в этом отношении выражения вроде: «Взвод сменяет караул» или «Меньшинство подчиняет большинство». Остроумно использовал двусмысленность выражения А.П. Чехов, вложив в уста одного из персонажей сообщение: «Перед вами череп обезьяны очень редкой разновидности. Таких черепов у нас всего два, один — в Национальном музее, другой — у меня».

Нельзя отождествлять различные мысли, нельзя тождественные мысли принимать за нетождественные. Результат применения — закон тождества обеспечивает определенность логического мышления.

Закон непротиворечия.

Закон непротиворечия (lex contradictionis) указывает на недопустимость одновременного утверждения (в рассуждении, в тексте или теории) двух суждений, из которых одно является логическим отрицанием другого, то есть суждений вида A и A или их конъюнкции, или эквиваленции, или — в более широком смысле — утверждений о тождестве заведомо различных объектов, поскольку обычно правила логики таковы, что позволяют из противоречия выводить произвольные суждения, что обесценивает содержательный смысл умозаключений или теорий. Наличие противоречия в рассуждении (теории) создаёт парадоксальную ситуацию и нередко указывает на несовместимость посылок, положенных в основу рассуждения (теории). Этим обстоятельством часто пользуются в косвенных доказательствах.

Закон исключнного третьего.

Закон исключённого третьего (lex exclusii tertii) на логическом языке записывается формулой A ⌵ A и утверждает, что нет ничего среднего (промежуточной оценки) между членами противоречивой пары (отсюда другое латинское название этого закона — tertium non datur). В методологическом плане этот закон выражает конструктивно неоправданную идею о разрешимости (потенциально осуществимом указании на истинность или ложность) произвольного суждения. В отличие от формулы, соответствующей закону противоречия, формула, соответствующая закону исключённого третьего, не выводима в интуиционистских и конструктивных исчислениях, хотя и неопровержима в них. Дихотомия установленных истины и лжи неоспорима, но дихотомия утверждения и отрицания оспаривалась неоднократно. Наиболее последовательную критику закона исключённого третьего дал Л. Э. Я. Брауэр. В свете его критики этот закон следует рассматривать только как принцип (или постулат) классической логики.

Фигура 1.

Barbara

A: Все хищные животные питаются мясом.

A: Тигры суть хищные животные.

A: Тигры питаются мясом.

Этот силлогизм символически можно изобразить следующим образом. «Хищные животные» как средний термин обозначим при помощи M; «питающиеся мясом» как больший термин – посредством P, а «тигры» – посредством S; тогда силлогизм изобразится при помощи схемы на рис. 23.

Celarent

E: Ни одно насекомое не имеет более трёх пар ножек.

A: Пчёлы суть насекомые.

E: Пчёлы не имеют более трёх пар ножек.

Схема этого модуса изображена на рис. 24.

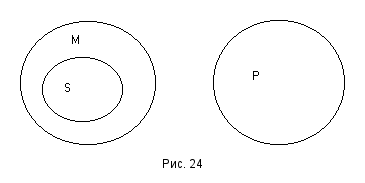
Darii

A: Все хищные животные питаются мясом.

I: Некоторые домашние животные суть хищные животные.

I: Некоторые домашние животные питаются мясом (рис, 25).

Ferio

E: Ни один невменяемый не наказуем.

I: Некоторые преступники невменяемы.

O: Некоторые преступники не наказуемы (рис. 26).

Фигура 2.

Cesare

E: Ни один справедливый человек не завистлив.

A: Всякий честолюбивый завистлив.

E: Ни один честолюбивый человек не есть справедлив (рис. 27).

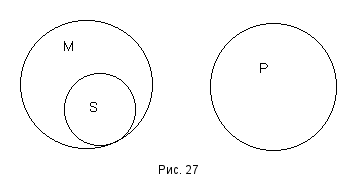
Camestres

A: Преступники действуют из злого намерения.

E: N. не действовал из злого намерения.

E: N не есть преступник.

Festino

E: Ни один благоразумный человек не суеверен.

I: Некоторые хорошо образованные люди суеверны.

O: Некоторые хорошо образованные люди неблагоразумны.

Baroko

A: Все истинно моральные действия совершаются из правильных мотивов.

O: Некоторые действия, благодетельные для других, не совершаются из таких мотивов.

O: Некоторые благодетельные для других действия не суть истинно моральные.

Фигура 3.

Darapti

A: Все киты суть млекопитающие.

A: Все киты живут в воде.

I: Некоторые живущие в воде животные суть млекопитающие.

Данное умозаключение относится к фигуре 3, где средний термин d обеих посылках является подлежащим. Меньший термин «живущие в воде существа» взят в меньшей посылке не во всём объёме; следовательно, и в заключении должен быть взят не во всём объёме (рис. 28).

Felapton

E: Ни один глухонемой не может говорить.

A: Глухонемые суть духовно нормальные люди.

O: Некоторые духовно нормальные люди не могут говорить (рис. 29).

Disamis

I: Некоторые романы поучительны.

A: Все романы суть вымышленные рассказы.

I: Некоторые вымышленные рассказы поучительны.

Ferison

E: Ни одна несправедливая война не может быть оправдана.

I: Некоторые несправедливые войны были успешны.

O: Некоторые успешные войны не могут быть оправданы.

Фигура 4. Возьмём силлогизм:

Bramantip

A: Все металлы суть материальные вещи.

A: Все материальные вещи имеют тяжесть.

I: Некоторые тела, имеющие тяжесть, суть металлы.

В этом силлогизме средний термин взят сказуемым в большей и подлежащим в меньшей посылке. Сказуемое в меньшей посылке взято не во всём объёме, поэтому и в заключении оно должно быть взято не во всём объёме. Таким образом, получается заключение: «некоторые тела, имеющие тяжесть, суть металлы». Эта фигура называется галеновской от имени Галена (в III в. н. э.); её не было у Аристотеля.

Ещё пример для иллюстрации четвёртой фигуры.

Camenes

A: Все квадраты суть параллелограмм.

E: Ни один параллелограмм не есть треугольник.

E: Ни один треугольник не есть квадрат.

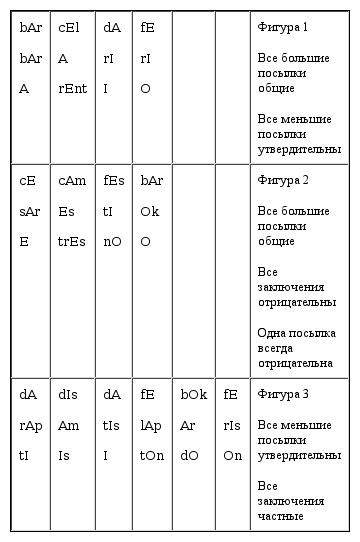
Характеристика фигур. Характеризуем в общих чертах все четыре фигуры силлогизма в отношении их познавательного значения.

Фигура 1. В ней меньшая посылка утвердительная, а большая общая (sit minor, affirmans, пёс major sit specialis). Эта фигура употребляется в тех случаях, когда нужно показать применение общих положений (аксиом, основоположений, законов природы, правовых норм и т.п.) к частным случаям; это есть фигура подчинения.

Фигура 2. В этой фигуре одна из посылок должна быть отрицательной и большая посылка должна быть общей (una negans esto, nec major sit specialis). Посредством этой фигуры отвергаются ложные дедукции, или ложные подчинения. Например, кто-нибудь утверждает относительно испытуемого газа, что он есть кислород. Нам стоит указать на какой-нибудь присущий кислороду признак, который не присущ испытуемому газу, для того чтобы убедиться в том, что это не есть кислород. Тогда у нас получится следующий силлогизм:

A: Кислород поддерживает горение

E: Этот газ не поддерживает горения.

E: Этот газ не есть кислород.

Кто-нибудь утверждает, что данное лицо больно лихорадкой; утверждая это, он производит подчинение. Нам нужно отвергнуть это подчинение. Тогда мы составляем следующий силлогизм:

A: Все больные лихорадкой испытывают жажду.

E: Этот больной не испытывает жажды.

E: Этот больной не болен лихорадкой.

Таким образом, по второй фигуре отвергаются ложные подчинения, и именно потому, что одна из посылок отрицательная. Юридические приговоры строятся по этой фигуре. Например:

A: Этот смертельный удар нанесён человеком, обладающим огромной силой.

E: Обвиняемый не есть человек, обладающий огромной силой.

E: Обвиняемый не нанёс смертельного удара.

Фигура 3. В фигуре 3 меньшая посылка должна быть утвердительной, а заключение должно быть частным (sit minor affirmans, conclusio sit specialis). Поэтому в фигуре 3 обыкновенно отвергается мнимая общность утвердительных и отрицательных суждений или доказывается исключение из общего положения. Положим, нам нужно доказать, что утверждение «все металлы твёрды» допускает исключение, что оно не всеобще. Тогда мы строим силлогизм по фигуре 3:

E: Ртуть не тверда.

A: Ртуть есть металл.

O: Некоторые металлы не твёрды.

Фигура 4 имеет искусственный характер и обыкновенно не употребляется.

Характер посылок и заключений каждой фигуры может быть наглядно представлен, если мы буквы модусов каждой фигуры расположим по вертикальным линиям таким образом, что буквы больших посылок будут идти по горизонтальной, буквы меньших посылок по второй горизонтальной и буквы заключений по третьей горизонтальной.

Развитие логики в России

По-видимому, первым оригинальным российским сочинением по логике стали «Письма к немецкой принцессе» (Lettres à une princesse d'Allemagne) Л.Эйлера, сначала вышедшие в трех частях в Санкт-Петербурге (1767–72) на французском языке, затем в Лейпциге (1770) и позднее переведенные на русский под названием «Письма о разных физических и философических материях» (СПб., 1796). Затем полвека о логике в России книг не писали (за исключением компилятивной «Логики» И.С.Рижского, 1790), ограничиваясь немецкими и французскими источниками. Только учреждение новых университетов (Тартуского, 1802; Казанского, 1804; Харьковского, 1805), расширившее возможности для философского образования (до этого времени лекции по философии читались только в Московском университете), благоприятно сказалось и на отношении к логике. Появляются местные сочинения: «Начертания логики» А.С.Лубкина (СПб., 1807), «Логика, риторика и поэзия» Ф.Мочульского (Харьков, 1811), «Логические наставления» Д.П.Лодия (СПб., 1815), «Логика» И.Любочинского (Харьков, 1817), «Опыт логики» П.Любовского (Харьков, 1818), «Начальные основания логики» И.И.Давыдова (М., 1820), «Краткое руководство по логике» Н.Рождественского (СПб., 1826).

В интеллектуальную жизнь российских университетов логика входила не самостоятельным предметом, а как приложение к тем или иным философским системам, которые в разное время преобладали. К примеру, весь 18 в. и нач. 19-го прошли под знаком вольфовской и кантовской философии. С 30-х гг. усиливается влияние диалектики Фихте, Шеллинга и Гегеля. Как и философия, логика плохо совмещалась с установками системы образования, принятой в России, поскольку обе они, всегда направленные на «изощрение умов», могли порождать скептицизм, не всегда обращаемый «на пользу православия и народности».

В этой ситуации стремление отделить логику от философии, представить ее как самостоятельную науку, лежащую вне идеологических интересов, казалось естественным. И первая заявка в этом направлении была сделана, по-видимому, К.Зеленецким в статье «О логике как систематически целом и как о науке, объясняющей факты Мышления и Знания» (1836), где он ратует за независимость формальной логики от философии.

Но потребовалось время, чтобы российская логика конституировалась в самостоятельную науку. Этому способствовали, во-первых, аналогичные процессы в Англии, Германии и во Франции, и, во-вторых, основательное знакомство русских логиков с достижениями логиков в странах Западной Европы. При этом было учтено все – и метафизическое направление германской логики (Р.Лотце, В. Шуппе, В.Вундт и др.), и психологическое направление этой логики (X.Зигварт, Т.Липпс), и индуктивное направление сторонников английского эмпиризма (Д.С.Милль, А.Бэн), и математическое направление тех же англичан (Дж.Буль, А.де Морган, Ст.Джевонс, Дж.Венн). Именно к кон. 19 в. (под влиянием работы К.Прантля) появляются российские исследования (обзоры) по истории логики М.И.Владиславлева (1872), М.М.Троицкого (1882), П.Лейкфельда (1890), дополняемые оригинальными суждениями этих авторов.

Вторая половина 19 в. – это время реформы логики, выхода за рамки аристотелевской силлогистики. В России эта реформа шла по двум направлениям. Во-первых, в философской логике М.Каринский (1880) предложил новую классификацию выводов (отличную от классификаций Аристотеля, Милля и Вундта), основанную на сравнительном анализе отношений тождества между субъектами и предикатами суждений, участвующих в выводе, а Л.Рутковский(1899) дополнил эту классификацию и развил критику миллевских индуктивных методов именно как методов логического доказательства. С.И.Поварнин (1917) обратил внимание на особенность несиллогистических умозаключений и пришел к выводу, что их теория возможна только на почве логики отношений, включающей и принципы логистики. Во-вторых, главная реформа шла в том направлении логики, которое позднее получило название математической (или символической) логики. Здесь следует указать на работы В.Бобынина (Опыты математического изложения логики. М., 1886); М.С.Волкова (Логическое исчисление. 1894), исследования И.В.Слешинского (Логическая машина Джевонса. 1893) и Е.Л.Буницкого (1896–1897), и, наконец, на классические работы П.С.Порецкого, в известной мере завершившие эпоху булевско-шрёдеровского развития алгебры логики как алгебры классов.

Между тем, не сталкиваясь с интересами сторонников математического направления в логике, продолжалось и развитие философской логики. Важный его период связан с творчеством Н.А.Васильева. Он выступил автором «воображаемой логики» (1910, 1912). Основная идея заключалась в том, что законы логические (см. Закон логический) подразделяются на два уровня: законы собственно логики, которая является эмпирической, и поэтому они вариативны, и законы металогики, которые неизменны. В мире эмпирических законов ни закон противоречия, ни закон исключенного третьего не являются универсальными. Васильев по праву считается вместе с польским логиком Я.Лукасевичем предшественником паранепротиворечивой логики. Он также стоит у истоков многозначной (точнее, трехзначной) логики. Воззрения Васильева опирались на общие философские идеи русской университетской логики, в которой, с одной стороны, в мире «вещей-в-себе» допускалась противоречивость, и выдвигалась проблема объемной неопределенности «качественных» понятий (А.И.Введенский, И.И.Лапшин), по сути дела ставившая под вопрос общезначимость исключенного третьего закона, а, с другой стороны, отвергалось аристотелевское (т.н. корреспондентское) определение истины, которому противопоставлялась непосредственная («интуитивная») данность субъекту познаваемого объекта «в подлиннике» (Н.О.Лосский). Настойчивыми логическими поисками отмечено и богословское творчество П.Флоренского, настаивавшего на неизбежной противоречивости (антиномичности) познания. Высылка из России в нач. 20-х гг. выдающихся представителей русской гуманитарной мысли и трагическая судьба многих из тех, кто остался в России, в корне изменили саму постановку проблемы о соотношении философии и логики.

Кризис оснований, захвативший математику в нач. 20-го столетия, затронул и логику. В работе «О недостоверности логических принципов» (1907) Л.Э.Я.Брауэр поставил вопрос о новой – интуиционистской логике. В России брауэровский скептицизм в отношении закона исключенного третьего разделял и одесский математик С.О.Шатуновский (1917). Когда к кон. 20-х гг. начались поиски формализации интуиционистски приемлемых способов рассуждений, интуиционизм нашел признание у логиков России. И это не случайно, поскольку многие из них входили тогда в Московскую математическую школу, возглавляемую Н.Н.Лузиным – выдающимся представителем «полуинтуиционистской» концепции в основаниях математики, известной под именем эффективизма. Результатом работы в этом направлении российских математиков А.Н.Колмогорова (1925, 1932) и В.И.Гливенко (1928–29) стали первые аксиоматические системы интуиционистской логики и первые теоремы о взаимоотношении между классической логикой и интуиционистской.

Логическим отражением поисков, родственных интуиционистским, явилась работа И.Е.Орлова «Исчисление совместности предложений» (1928), которая оказалась исторически первой в мире работой по релевантной логике. Философская мотивировка этой работы была дана им еще в 1925 в статье «Логические исчисления и традиционная логика». Она сводилась к идее необходимости выражения в логическом формализме «связей по смыслу» между основанием и следствием условного суждения (а следовательно, и содержательного отношения между элементами умозаключения) и была для него выражением своеобразно понятой диалектической логики.

Выдающимся достижением этого периода является также серия статей И.И.Жегалкина (1927–29) по арифметизации символической логики высказываний и предикатов и решение им (в рамках этой арифметизации) проблемы разрешимости для логики одноместных предикатов (для аристотелевской логики). Интерпретируя логику высказываний как «арифметику четного и нечетного», Жегалкин сводит значительный корпус доказательства теорем знаменитой «Рrinсіріа mathematica» (Уайтхеда и Б.Рассела) к простым арифметическим упражнениям.

Новое направление было открыто в эти же годы московским логиком М.И.Шейнфинкелем. В статье «О кирпичах математической логики» («Mathematische Annalen», 1924) он заложил основы комбинаторной логики.

Тогда же русский физико-химик А.Р.Щукарев предпринял попытку применить понятия дифференциального исчисления к логике, основываясь на философии Р.Авенариуса. Щукарев публично демонстрировал сконструированную им «логическую машину» (аналог машины Джевонса).

Однако к кон. 20-х гг. и математическая логика оказалась под огнем партийной критики. Формальной логике в целом в «директивном» порядке была противопоставлена диалектическая логика. Преподавание формальной логики в школах и высших учебных заведениях прекращается. Даже математики (во избежание обвинений в буржуазном идеализме) отходят от идеалов своей молодости. Активными борцами против «идеализма в математике» в эти годы становятся Э.Кольман и С.А.Яновская. Позднее к этому дуэту присоединится В.Н.Молодший.

С этого времени и до кон. 40-х гг. логическая мысль в СССР развивается исключительно в рамках математики. В математических журналах появляются работы Д.А.Бочвара, А.И.Мальцева, П.С.Новикова, В.И.Шестакова и др., несущие на себе высокую степень математической кодификации языка и этим предохраняющие их авторов от идеологических нападок.

В 1946 постановлением ЦК ВКП(б) логика в ее традиционной форме вводится как предмет преподавания в школах и вузах. В этом же году переиздается дореволюционный учебник по логике Г.И.Челпанова (с купюрами, сделанными по «идеологическим соображениям»), появляются оригинальные учебники В.Ф.Асмуса (1947), К.С.Бакрадзе (1951) и др. Логика восстанавливается как особое направление гуманитарного образования в вузах, на ряде факультетов университетов и педагогических институтов открываются кафедры логики. В 1947 созданы кафедры логики на философском факультете МГУ (возглавил ее П.С.Попов) и ЛГУ (первым преподавателем логики уже в 1944 был С.И.Поварнин); в том же году образован сектор логики в Институте философии Академии наук СССР (ныне РАН).

Начало 50-х гг. отмечено рождением российского конструктивизма (см. Конструктивное направление). Работы А.А.Маркова и сотрудников его школы в немалой степени способствовали утверждению в общественном сознании научной значимости формальной логики. В эти годы С.А.Яновская инициирует издание на русском языке ведущих трудов по современной логике: Д.Гильберта и И.Аккермана «Основы теоретической логики» (1947) и А.Тарского «Введение в логику и методологию дедуктивных наук» (1948). Созданная ею школа логики оказала (благодаря обилию ее учеников) большое влияние на развитие философской мысли, на взаимодействие между логиками-философами и логиками-математиками. Семинар С.А.Яновской (кон. 50-х – нач. 60-х гг.) воспитал не одно поколение логиков. Большая роль принадлежит в этом также и А.А.Маркову, возглавившему образованную в 1958 кафедру математической логики МГУ. На логических семинарах Яновской, Маркова и их учеников (механико-математический и философский факультеты МГУ), Н.А.Шанина (в ЛГУ), на секторе логики Института философии формируется отечественная школа логиков-философов.

Определенным итогом описанного развития (и, конечно, относительно либеральной атмосферы 60-х гг.) явилось издание первой в России «Философской энциклопедии» (1960–70), в которой логика, несмотря на сопротивление некоторых членов редакционной коллегии энциклопедии и даже ее главного редактора, впервые в истории отечественной философской мысли была представлена в ее современном (на момент издания) и по возможности полном виде.

Б.В.Бирюков, M.M.Новосёлов

Уникальная история России 20 в. предопределила и уникальное развитие логики в ней, во многом непонятное для западного историка науки. В тоталитарной социальной системе логика стала объектом чисто идеологических манипуляций. Даже после того, как в 1947 формальная логика была возвращена в систему среднего и высшего образования, ее положение в этой системе не было независимым. В результате острой дискуссии в 1950–51 гг. на страницах главного философского официоза «Вопросы философии» и дискуссии по проблемам логики в МГУ и Институте философии АН СССР (ныне РАН) было зафиксировано, что высшей ступенью мышления является диалектическая логика, а низшей – формальная. Сторонников последней такое соотношение явно не устраивало и на этом фоне все 50-е и даже 60-е гг. прошли в обоюдной полемике. С одной стороны, в целях примирения сторон некоторыми участниками дискуссии предпринимаются попытки придать диалектической логике разумный смысл (С.А.Яновская, А.А.Зиновьев, Д.П.Горский, И.С.Нарский и др.). С другой стороны, в целях преодоления известного несоответствия уровней тогдашнего логико-философского образования и мировой логической культуры устанавливается практика переводов важнейших трудов по философской логике, таких, как «Логико-философский трактат» Л.Витгенштейна (1958, общая редакция и предисловие В.Ф.Асмуса) и «Значение и необходимость» Р.Карнапа (1959, общая редакция Д.АБочвара, предисловие С.А.Яновской); а также фундаментальных трудов по современной математической логике (под редакцией В.А.Успенского), таких, как С.К.Клини «Введение в метаматематику» (с добавлениями А.С.Есенина-Вольпина, 1957) и А.Чёрча «Введение в математичес