Рациональность постнеклассической науки
Уже в неклассической науке практически снимался вопрос о двойственном видении движения мира и его объектов. Все объекты, процессы, явления уже в научной неклассике рассматривались как неизолированные, целостные, открытые системы. Но все-таки оставался нерешенным вопрос о том, каким это образом мир и его объекты организуются в системы, метасистемы и др. В этом случае как бы «за кадром» всегда остается указание на то, что мир и его объекты сотворены внешними силами. С созданием синергетики данная проблема в своей самой основной части снимается. Наука в постнеклассическом облике может ответить на философские вопросы относительно происхождения «ens per se» и «ens commune». Более того, синергетика выполняет функции не только звена второго уровня общенаучного знания. На ее основе можно понять самоорганизующуюся связь различных типов детерминации как в сфере какого-то конкретного «слоя бытия», так и между этими «слоями». Иными словами, она становится мощным инструментом междисциплинарных исследований. Тем самым научная рациональность приобретает новую «степень целостности». Эта более высокая целостность также является важнейшей отличительной чертой постнеклассической рациональности науки (по отношению к неклассической). И еще один момент. Ввиду нового уровня целостности рациональность научной постнеклассики приобретает возможность отражать своего рода голографичность как всеобщей универсальной детерминации, так и детерминации в «слоях бытия». Это и означает, что в мире все частицы «видят» каждую, а каждая «видит всех». Особенно это проявилось в концепции голографической Вселенной Д.Бома, голографического мозга Прибрама и др. Возможность отразить эту голографичность снимает проблему различных «центризмов», против которых вполне обоснованно выступают постмодернисты. Одна из главных целей данного параграфа состоит в указании на новые, ранее недоступные науке возможности целостного рассмотрения проблем сразу по всей картине всеобщей детерминации (начиная от микро- и кончая макро- и мегамиром).
Но прежде чем обратиться к этому, есть смысл взглянуть на то, как предлагаемый в монографии подход к рациональности научной постнеклассики соотносится с уже имеющимися подходами в отечественной философской литературе. Лучше всего это делать, осмысливая взгляды того, кто ввел в отечественную литературу термин «постнеклассическая наука». Речь идет о концепции В.С.Степина, который считает, что критерий обсуждаемой ступени развития науки многоуровневый. В частности, он пишет, что на данной ступени реализуются комплексные научные программы, что «порождает особую ситуацию сращивания в единой системе теоретических и экспериментальных исследований, прикладных и фундаментальных знаний, интенсификацию прямых и обратных связей между ними» [209,627].
Следующие же характеристики, предлагаемые В.С. Степиным, а именно: формирование разными науками целостной общенаучной картины мира, влияние на неё междисциплинарных исследований, системное видение в таких исследованиях тех феноменов, которые оказались недоступными или малодоступными в границах отдельных дисциплин, не противоречат и хорошо согласуются с критерием, предложенным в настоящей работе. Столь же хорошая согласованность наблюдается и в том, что объектами «современных междисциплинарных исследований все чаще становятся уникальные системы, характеризующиеся открытостью и саморазвитием. Такого типа объекты постепенно начинают определять характер предметных областей основных фундаментальных наук, детерминируя облик современной постнеклассической науки» [209,628].
В безусловном согласовании с предлагаемыми в моей работе подходами находятся и те грани постнеклассицизма науки, которые характеризуются тем, что наука начинает рассматривать сложные исторически развивающиеся системы на основе синергетических методов и сложного компьютерного моделирования. Это же относится и к исследованию сложных развивающихся человекоразмерных систем, где в научную рациональность должны быть эксплицированы ценности общесоциального характера. «В современных программно-ориентированных исследованиях эта экспликация осуществляется при социальной экспертизе программ. Вместе с тем в ходе самой исследовательской деятельности с человекоразмерными объектами исследователю приходится решать ряд проблем этического характера, определяя границы возможного вмешательства в объект. Внутренняя этика науки, стимулирующая поиск истины и ориентацию на приращение нового знания, постоянно соотносится в этих условиях с общегуманистическими принципами и ценностями. Развитие всех этих новых методологических установок и представлений об исследуемых объектах приводит к существенной модернизации философских оснований науки» [209,631-632]. Именно это и имеется в виду, когда В.С.Степин в краткой форме характеризует критерий постнеклассицизма науки. Он пишет: «Постнеклассический тип рациональности расширяет поле рефлексии над деятельностью. Он учитывает соотнесённость получаемых знаний об объекте не только с особенностью средств и операций деятельности, но и с ценностно-целевыми структурами. Причем эксплицируется связь внутринаучных целей с вненаучными, социальными ценностями и целями» [209,634].
Из всего изложенного следует, что предлагаемый мною критерий постнеклассицизма науки отражает не все грани этой ступени её развития, на которые обратил внимание В.С. Степин. Но, во-первых, этот критерий не противоречит, а напротив, хорошо согласуется с названными гранями. А, во-вторых, в моей работе ставится задача детального обсуждения одного из наиболее существенных «механизмов» внутренней логики самой науки как системы знания, поскольку именно данный «механизм» дает возможность науке как подняться на новую ступень развития, так и выполнять те функции, которые требуются от нее на этой ступени.
Прежде чем обсуждать новые возможности науки, вернемся к упомянутой в предыдущем параграфе постнеклассичности математики. Первой ступенью этой постнеклассичности послужил унитарный облик математики, полученный Бурбаки. Но этот облик был выстроен на основе структур. А последующее развитие, в ходе которого сложились уже упомянутые поливариантные облики унитарности математики, было связано с теорией категорий и функторов и с концепцией нечетких множеств Заде. Интересным здесь является то, что теория категорий и функторов, равно как и концепция нечетких множеств Заде, сложилась уже в период постнеклассической математики (наука при этом была еще в неклассическом состоянии), но особый интерес к ним был проявлен в период становления постнеклассической науки. В самом деле, первая работа Заде по нечетким множествам вышла в 1965 году. В более модифицированном виде она предстала уже в семидесятые годы. Поначалу работы Заде были в достаточной степени прохладно приняты в США. Но уже в восьмидесятые годы концепция нечётких множеств стала одной из наиболее популярных среди тех, кто занимается сложными компьютерными моделями с применением концепции нейросетей и синергетических подходов.
Характерной особенностью уже постнеклассического периода в развитии математического знания является также кратко упомянутая в предыдущем параграфе гибридизация структур, которая невозможна без сложных компьютерных моделей. Можно, например, еще раз обратиться к «дифференциальной динамике», появившейся как гибрид дифференциальной топологии, теории дифференциальных уравнений и теории вероятностей. В ходе становления новых математических «гибридных» структур компьютерные модели являются и инструментом построения, и средством применения, и критерием строгости полученных результатов. Ясно, что на этом пути компьютерное моделирование может строиться как на основе теории Г.Кантора, так и на основе нечетких множеств Л.Заде, в зависимости от целей, преследуемых в создании тех либо иных структур.
Если же обратиться к теории категорий и функторов, то интерес к ним резко возрос лишь в семидесятые годы XX в., хотя работы по их созданию начались еще в послевоенный период (1945-1955 гг.) усилиями С.Эленберга и С.Маклейна. В настоящее время теория категорий и функторов, по сути дела, является основанием поливариантного облика унитарности математики [140, 92-99]. На такой новой базе, дающей возможность получать в более гибкой форме, чем на основе структур поливариантные облики унитарности математики при построении её подсистем с помощью сложного компьютерного моделирования с применением нечетких множеств Заде, можно получить математическую картину всеобщей универсальной связи, где каждый облик (из всего спектра поливариантности) как бы отражает всеобщую универсальную связь. Все эти облики «перекликаются», будучи неизолированными, что и позволяет отразить многообразие её развития.
Итак, сущность изложенного сводится к тому, что новый уровень целостного видения «всего поля» детерминации дает науке возможности проводить ранее ей недоступные исследования, когда связываются проблемы микро- и мегамира, а также фундаментальные проблемы, имеющие прямое отношение не только к науке, но и к философии.
Примером того, как избранное направление в исследовании на сформированном наукой горизонте касается сразу нескольких проблем разных уровней, может послужить работа И.Пригожина (написанная в соавторстве с его сотрудницей И.Стенгерс) «Время, хаос, квант. К решению парадокса времени» [174]. В данной работе И. Пригожин рассматривает сразу три, казалось бы, очень разных парадокса: парадокс времени, квантовый парадокс и космологический парадокс. Это и есть целая научно-исследовательская программа. «Ядром» обсуждения является парадокс времени. Его суть в том, что реальное время необратимо. Основание такой необратимости – эволюция всеобщей универсальной связи, идущая по принципу «свободно становящейся последовательности». Каждому моменту времени соответствует своя «картина» всеобщей универсальной связи. Возврат в обратную сторону и по тому же «сценарию» в принципе невозможен. В то же время в физических теориях классической и даже неклассической физики «инверсия» времени вполне допустима. Получается, что самая передовая отрасль современного естествознания (физика) не может отразить реально существующий факт – необратимость времени. Собственно говоря, в этом и состоит суть парадокса времени, как его понимает И.Р.Пригожин. (Парадокс времени разными авторами, как известно, понимался по-разному. К нему обращались, например, Аристотель, Августин и др. В данном случае нет необходимости обсуждать их взгляды, хотя они представляют несомненный интерес.)
Предложение И.Р.Пригожина по решению обсуждаемого парадокса вполне в духе постнеклассической науки. Просто другому уровню её развития такое решение не под силу. И.Р.Пригожин учёный, и, естественно, он пользуется терминологией, сложившейся в науке. Далее следует сделать несколько предварительных замечаний. Уже отмечалось, что под хаосом и неклассическая, и постнеклассическая наука понимают влияние всего внешнего окружения на данную неизолированную систему. Наука исследовать сразу всё это внешнее влияние не в состоянии и потому даёт ему своё название – хаос. Другими словами, бытовой и научный смысл одного и того же понятия оказывается различным. Итак, если некие системы рассматриваются как принципиально хаотические, то это значит, что они являются принципиально неизолированными. И.Р.Пригожин делает очень существенное заявление: хаотические системы имеют принципиально вероятностный характер. В терминологии И.Р.Пригожина – это «несводимое вероятностное описание». Вот именно под этим углом зрения можно увидеть хорошую согласованность приведённого мною подхода к онтологическому аспекту вероятности и взглядов И.Р.Пригожина. Действительно, если иметь в виду, что онтологическим основанием вероятности является неизолированная и в то же время целостная системность во взаимодействиях, то становится понятным, почему движение принципиально неизолированных систем имеет принципиально вероятностный характер («несводимая вероятность»). И.Р.Пригожин по этому поводу, в частности, пишет: «В данном контексте вероятность выступает не как порождение нашего незнания, а как неизбежное выражение хаоса» [174,9]. Но принципиально вероятностные, то есть принципиально неизолированные системы, являются нелинейными. И вся всеобщая универсальная связь также является таковой. Другими словами, для отражения её «поведения» нужны и нелинейные методы. Фазовое 6N-мерное пространство фактически является линейным гильбертовым пространством. Собственно говоря, отражение движения нелинейных систем на основе линейного пространства и порождает как парадокс времени, так и квантовый парадокс. В своё время на подобную ситуацию в исследовании объектов микромира обратил внимание А. Эйнштейн. Он подчеркнул, что окружающий нас мир принципиально нелинеен. А учёные пытаются его исследовать линейными методами. Делают они это лишь потому, что не умеют решать нелинейные уравнения. И, добавим от себя, не имеют математического аппарата для отражения принципиальной нелинейности пространства всеобщей универсальной связи. Можно в этой связи процитировать И.Р.Пригожина, который пишет, что «в ортодоксальной квантовой механике пространство, в котором происходит эволюция волновых функций, гильбертово. То же гильбертово пространство имеет фундаментальное значение для статистического описания в терминах ансамблей… Мы покажем, что хаос вынуждает нас отказаться от гильбертова пространства и перейти к обобщенным пространствам (часто называемым «оснащенными» пространствами), структура которых зависит от конкретной формы неустойчивости. Таким образом, эволюцию распределения вероятности следует рассматривать в пространстве, которое зависит от динамики. Решение парадокса времени, как и других парадоксов (квантового и космологического – С.А.), возможно только потому, что пространство становится «темпорализованным», поскольку прошлое и будущее играют не одну и ту же роль» [174,17]. Иными словами, И.Р.Пригожин нашел математический аппарат для отражения изменения во времени картины всеобщей универсальной связи. И хотя это, по-видимому, не самый совершенный инструментарий такого отражения, но на сегодняшний день он, пожалуй, является пока единственным. Имеется в виду, что этот инструментарий хорошо адаптирован к современной науке и он может применяться в ней прямо сейчас. Смысл предыдущего утверждения состоит также и в том, что, конечно же, наука найдет и другие методы исследования обсуждаемой нелинейности пространства и объектов, в нем движущихся. Но для этого, естественно, нужны время и новые поиски. Безусловной заслугой И.Р. Пригожина является то, что он увидел, что такой математический аппарат уже имеется в современной математике, и сумел им воспользоваться в своих исследованиях. Речь идет о работах М.А. Гельфанда. По этому поводу И.Р. Пригожин пишет, что «обобщенные («оснащенные») пространства были впервые введены в математическую литературу М.А. Гельфандом и его коллегами в 60-е годы. Взаимосвязь между оснащенными пространствами и хаосом была понята совсем недавно» [174,17].
Фактически, на доступном для данной модели уровне удается отобразить «обобщенную» связь координат пространства. И тогда получается, что каждому моменту времени соответствует своя связь или своя «картина» связи этих координат. В известном смысле появляется возможность отразить своего рода свободно становящуюся (Л.Брауэр) последовательность «рисунков» в этой «картине». Что, собственно говоря, и соответствует тому, что происходит в реальной всеобщей универсальной связи.
На основе концепции «оснащенного» пространства М.А.Гельфанда в обсуждаемой работе предлагается оригинальное решение «квантового парадокса». Под таким парадоксом И.Р.Пригожин понимает, с одной стороны, так называемый «коллапс» волновой функции, который как бы нужен для того, чтобы перейти от амплитуд вероятности, представленных в этой функции, к самим вероятностям. В частности, он пишет, что «двойственная структура квантовой механики – волновая функция и ее коллапс – приводит к концептуальным трудностям и спорам, продолжающимся с момента возникновения квантовой механики на протяжении вот уже более шестидесяти лет. Хотя квантовую механику с полным основанием называли наиболее успешной теорией, ей так и не удалось выяснить физическую природу «коллапса». Многие физики пришли к заключению, что ответственность за коллапс несет наблюдатель и производимые им измерения. В этом и заключается квантовый парадокс, вводящий субъективный элемент в наше описание природы» [174,10].
Как это все можно представить в том методологическом подходе, который развивается автором в данной монографии? Волновая функция, на самом деле, является очень изящным инструментом отражения поведения неизолированной системы. Дело в том, что с помощью теории колебаний и волн (хроматических и ахроматических), действительно, можно легко формализовать поведение таких систем, поскольку влияние внешнего окружения на систему так и выглядит, как колебание узлов целостности, параметров целостности системы около собственных положений устойчивости. Поэтому на основе теории колебаний можно отразить даже феномен самоорганизации в неизолированных системах. Так, в частности, и было сделано исследователями школы А.А.Андронова. И, естественно, с помощью волновых уравнений можно отразить не только «раскачивание» непосредственных параметров неизолированной системы внешним окружением, но и величины вероятностей такого «раскачивания», что и наблюдается в волновом уравнении Шредингера. С некоей субъективной интерпретацией операции «коллапса» можно было бы и примириться, что, вообще говоря, и делалось «более шестидесяти лет», если бы не другие моменты. Волновая функция считается бесконечной в пространстве (и в сторону «прошлого» и в сторону «будущего»). Она вроде бы и отвечает неизолированности и вероятностности систем окружающего мира (поскольку отражает и в одну, и в другую сторону «волны вероятностей» и «амплитуды» этих вероятностей). Но все же это отражение «линейное». И вот почему. В нем заранее принимается предпосылка о том, что окружающие нас в реальном мире системы не будут меняться, а всего лишь будут «влиять» друг на друга. Иными словами, картина всеобщей связи здесь «застывает» в изменении своего уже сложившегося вероятностного «рисунка». Говоря точнее, квантовая механика как бы «наполовину» нелинейна в облике волновой функции. А эта нелинейность должна стать полной, то есть должен все время меняться вероятностный рисунок всеобщей универсальной связи. Но вот это и недоступно такому «инструменту», как единичная «волновая функция». Здесь нужны своего рода ансамбли волновых функций, представляющие собой «континуумы» их «переплетений». В этой связи И.Р. Пригожин пишет, что «теперь мы можем дать реалистическую интерпретацию квантовой теории. Поскольку описание квантовых хаотических систем производится не в терминах волновых функций, а в терминах вероятностей, отпадает необходимость в «коллапсе волновой функции». Мы подробно покажем, как волновая эволюция хаотических систем трансформирует волновые функции в ансамбли. Именно квантовый хаос (единство неизолированных и в то же время целостных систем – А.С.), а не акт наблюдения опосредствует наш доступ к природе» [174,10]. И далее он подчеркивает, что такой подход, по сути дела, приводит к «несводимому вероятностному описанию, которое не может быть сведено к изучению отдельных волновых функций. Такие системы мы называем хаотическими. Приведенное определение хаоса охватывает классические и квантовые системы. В обоих случаях оно отнюдь не означает, что фундаментальные уравнения (Ньютона или Шредингера) утрачивают силу и становятся неприменимыми. Нет, из нового определения следует, что в общем случае невозможно вывести из этих уравнений заключение о поведении отдельных траекторий или отдельных волновых функций. Эволюция хаотических систем во времени требует несводимого вероятностного описания» [174,15].
Развиваемый И.Р. Пригожиным подход решает сразу несколько проблем квантовой механики, а не только проблему «коллапса» волновой функции. В самом деле, в этом случае не возникает так называемых «расходимостей», вследствие которых нужна не менее механистичная операция «перенормировки» волновой функции (предложенная в свое время японским физиком С.Саката). И это еще не все. Получает свое решение (правда, И.Р. Пригожин не пишет об этом в своей работе) очень известный парадокс Эйнштейна-Подольского-Розена. Суть его в том, что неясен механизм согласования волновых функций частиц после их взаимодействия. Дело в том, что во всеобщей взаимообусловленности процессов и явлений материального мира все элементарные частицы связаны друг с другом и до, и после их прямого взаимодействия. Они связаны и тогда, когда такого взаимодействия нет и, возможно, не будет. Но эту всеобщую взаимообусловленность саму по себе и связь в ней частиц друг с другом нельзя отразить ни 6N-мерным гильбертовым пространством, ни единичными волновыми функциями. И.Р. Пригожин предлагает обратиться соответственно к «оснащенным» пространствам М.А.Гельфанда и к ансамблям волновых функций. Таким образом, Эйнштейн, Подольский и Розен правильно ставили вопрос. Связь между частицами после взаимодействия остается. Но в то время в аппарате физической науки действительно не было механизма для характеристики сущностных моментов этой связи.
И, наконец, Пригожин ведет в своей работе обсуждение еще одного парадокса - космологического. Суть его состоит в том, что наиболее популярная в настоящее время «стандартная» модель Вселенной (модель Леметра) построена на концепции Большого Взрыва, согласно которой «рождение» Вселенной произошло примерно 15 млрд. лет назад. Иными словами, 15 млрд. лет назад взорвалась некая сингулярность, в которой плотность материи и энергии была бесконечной. Но если это так, то что было до Большого Взрыва? Наука на этот вопрос ответить не может. Но тогда получается, что не было и времени. Сам И.Р. Пригожин об этом, в частности, пишет: «Мы упомянули третий парадокс: космологический парадокс. Современная космология приписывает нашей Вселенной возраст: Вселенная родилась в результате Большого Взрыва около 15 миллиардов лет назад. Ясно, что это было событием. Но в традиционную формулировку законов природы события не входят. Траектории или волновые функции не начинаются и не кончаются. Вот почему гипотеза Большого Взрыва поставила физику «перед ее величайшим кризисом». Стивен Хокинг и другие высказали предположение о том, что Большой Взрыв мог иметь чисто геометрический характер. В геометрической Вселенной время было бы «акцидентом». Космологическое время было бы иллюзией: различие между временем и пространством, проводимое общей теорией относительности Эйнштейна, исключалось путем введения «мнимого» времени, которое должно было рассматриваться как реальное. Именно это мы имеем в виду, когда говорим о «космологическом парадоксе». Такой подход привел бы к окончательному уничтожению связи между бытием и становлением. Как пишет Хокинг о Вселенной, «она просто должна быть, и все!»» [174, 11]. И далее. «Однако существующие ныне космологические модели приводят к определенным концептуальным трудностям. Взять хотя бы Большой Взрыв. Он является неизбежным результатом «стандартной модели», доминирующей в современной космологии. Из этой модели следует, что, возвращаясь вспять во времени, мы неизбежно наталкиваемся на особую точку – сингулярность, в которой сосредоточена вся энергия и материя Вселенной. Таким образом, стандартная модель связывает начало Вселенной с особой точкой. Но стандартная модель не позволяет нам описывать эту особую точку, поскольку законы физики не применимы к точке, соответствующей бесконечной плотности материи и энергии. Неудивительно, что Джон Уиллер говорит о кризисе, с которым столкнулась физика!» [174,217].
В решении данного парадокса И. Пригожин предлагает оригинальную концепцию. Она состоит в том, что до сингулярности Вселенная представляла собой физический вакуум Г. Минковского. Сам физический вакуум все время находится в неравновесном состоянии и постоянно «флуктуирует». Если глобальная флуктуация превышает по уровню энергии 50 планковских масс (планковская масса равна 10-5г), то начинается самопроизвольный переход физического вакуума в вещество. Вот этот переход и произошел 15 млрд. лет назад. Данный процесс, согласно концепции И.Р.Пригожина, характеризуется возникновением частиц, имеющих массу, равную планковской массе (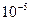 
г). Такие частицы долго существовать не могут. Они тут же коллапсируют, превращаясь, таким образом, в так называемые «черные мини-дыры». Последние, в свою очередь, также являются нестабильными. Их распад сопровождается выбросом большого количества элементарных частиц и столь же большого количества энергии. В момент «рождения» «черных мини-дыр» Вселенная расширяется экспоненциально (в соответствии с моделью В. де Ситтера). После их распада аттрактор развития Вселенной, по Пригожину, меняется. И она уже расширяется согласно стандартной модели.
Конечно же, концепция И.Р. Пригожина сложилась не на пустом месте. Целый ряд исследований уже был проведен. И об этом говорит сам И.Р.Пригожин. Но до него не было видения их всех в едином контексте. Так, идея рождения Вселенной из вакуума Минковского была предложена в моделях таких авторов, как Браут, Энглерт, Гунциг, Нардоне и Шпиндель. И. Р. Пригожин, в частности, пишет, что «их работы были первыми до модели инфляционной Вселенной, в которых вводилась идея экспоненциального роста размеров Вселенной как следствие неустойчивости вакуума Минковского. Кроме этого, в этих работах была продемонстрирована возможность «самосогласованной космологии», исключающей особую точку Большого Взрыва» [174,240]. В свою очередь, «инфляционная» модель была предложена (Р. Х. Бранденбергер – 1985 г., А. Д. Линде – 1984 г.) для того, чтобы объяснить необычайную однородность и изотропность реликтового излучения. В «инфляционной» модели «вводится второе рождение Вселенной примерно через 10-35c после Большого Взрыва…. Именно второе рождение Вселенной приводит к нарушению симметрии между сильным взаимодействием, с одной стороны, и слабым и электромагнитным, с другой. Второе рождение должно сопровождаться гигантским расширением (более чем в 1050 раз за интервал времени, не превышающий 10-32 с). В ходе этого расширения размеры Вселенной увеличиваются экспоненциально. Именно поэтому предложенная модель получила название инфляционной» [174,227].
Каким же образом из вакуума Минковского может «рождаться» Вселенная? Эту проблему, как пишет И. Пригожин, обсуждал в свое время (1973 г.) Эдвард Трайон, который считал, что « энергия встречается во Вселенной в двух формах. Существует энергия, связанная с гравитацией (соответственно с притяжением), и энергия, связанная с массой знаменитой формулой Эйнштейна E=mc2.… Отсюда напрашивается вывод, что наша Вселенная, состоящая из массы и энергии, может обладать нулевой общей энергией, как пустая Вселенная – вакуум Минковского. Действительно, нулевая полная энергия может образовываться и как сумма двух нулей (пустая Вселенная), и как сумма двух равных, отличных от нуля величин с противоположными знаками (материальная Вселенная). Иначе говоря, переход Вселенной из небытия в бытие может не сопровождаться изменением энергии. По мнению Трайона, наша Вселенная могла спонтанно образоваться именно по такому сценарию – из ничего, в результате (спонтанной) флуктуации вакуума» [174,229].
И все же на вопрос, как именно из физического вакуума рождается Вселенная, ни одна из названных моделей не отвечает. Вот этот механизм рождения, а именно: рождения частиц (с массой, равной планковской массе 10-5г), которые были названы «черными мини-дырами», и предложил И.Р. Пригожин. И не только предложил, но и обосновал, фактически связав в единую картину все идеи предыдущих космологических гипотез, начиная с модели Браута, Энглерта, Гунцига, Нардоне, Шпинделя, с инфляционной модели и кончая так называемой моделью «бесплатного обеда» Трайона. В концепции И.Р. Пригожина удалось также связать идеи В.де Ситтера и позитивные грани стандартной модели (исключая, конечно, собственно сам Большой Взрыв).
И хотя концепция И.Р. Пригожина по его же собственному признанию, далеко не совершенна, она все-таки стоит на более высоком, безусловно, уровне, нежели все предыдущие.Однако при этом на каждый решаемый вопрос как бы накладывается новый (а то и несколько), который раньше не был виден или недостаточно четко просматривался. Но это уже особенность научного познания. Можно привести хотя бы некоторые из возникающих уже на новом уровне проблемы. Если процесс рождения и распад «черных мини-дыр» закончился 15 млрд. лет назад, то чем же тогда можно объяснить рост энергии во Вселенной и лавинообразное нарастание в ней обычных элементарных частиц. Ученые сейчас наблюдают возникновение новых и сверхновых звезд. Откуда они берутся? Очень может быть, что это результат флуктуаций физического вакуума, приводящих к возникновению не Вселенной, а звезды. В этом случае, естественно, должен наблюдаться, помимо энергетического всплеска во Вселенной, еще и рост элементарных частиц.
В своей работе И.Пригожин пишет, что исследование феноменов «черных дыр» указало на их важнейшую особенность. «Черные дыры действуют как своеобразные термодинамические преобразователи: они поглощают все, что попадает в область их действия…и преобразуют в тепловое излучение» [174,231]. « Если говорить более точно, то Хокинг показал, что черные дыры распадаются, испуская тепловое излучение (излучение Хокинга) вполне определенной температуры» [174,230]. И, наконец, «до сих пор, насколько нам известно, излучение Хокинга не было наблюдаемо, тем не менее, оно рассматривается как необходимое следствие комбинации квантовых понятий и релятивизма» [174,231]. Иными словами, если сказанное относится ко всем «черным дырам» (и «мини» и «макси»), то ситуация предстает следующим образом. Процесс массового образования «черных мини-дыр» закончился около 15 млрд. лет назад. Хотя без него или похожего на него процесса сейчас, по-видимому, также не обходится. Во всяком случае, свидетельства этому могут быть в феномене звезд. Это очень высокие энергии, локализованные в пространстве и, естественно, в среде физического вакуума. Очень может быть, что вакуум как бы поддерживает звезду в состоянии равновесия (своего рода синергетика) путем «рождения» частиц высоких энергий и их распада. Но катаклизмы, случающиеся со звездами (взрывы новых и сверхновых звезд), – это нарушение равновесия. И в данном процессе взаимодействие звезд с вакуумом играет важную роль. Это и есть те моменты, которые, как пишут известные исследователи, пока не изучены в «поведении» звезд [239].
Вот такого рода локальными процессами, по-видимому, и можно объяснить рост энергии в расширяющейся Вселенной и рост в ней числа обычных элементарных частиц. Но, в свою очередь, есть ведь и просто черные дыры – следствие коллапса звезд. Они тоже излучают энергию. И их распад также связан с ее выбросом и выбросом обычных элементарных частиц. Можно предположить, что излучение Хокинга не обнаружено прямо, поскольку не является направленным. И вот здесь очень интересным может быть вывод, полученный также постнеклассической наукой. Имеется в виду вывод школы А. А. Самарского – С. П. Курдюмова о том, что тепловая энергия в Галактике не рассеивается беспорядочным образом. Срабатывают синергетические «механизмы». Энергия удерживается в границах своего рода «теплового кристалла» [102]. Безусловно, эти «тепловые кристаллы» Галактик пересекаются друг с другом и тем самым являются неизолированными. Безусловно, также и то, что связь между ними является системной и в то же время нелинейной. И, скорее всего, она влияет на реликтовое излучение, которое, как известно, идет отовсюду и во всех направлениях однородно и изотропно. Однако как они связаны друг с другом? Пока строгого ответа на данный вопрос нет. Но наличие этой связи – факт совершенно очевидный. Сохраненная в «тепловом кристалле» Галактики энергия должна пребывать в нем распределенной однородно и изотропно.
Весьма интересно то, что в постнеклассической науке «поле исследований» видят все, но вот научно-исследовательские проекты («парадигмы») выдвигают отдельные ученые, очень часто не спрашивая друг друга. «Аттракторы» этих проектов нередко пересекаются. И вот места этих пересечений бывают очень показательными. Они как бы сводят воедино разные слои в наблюдаемом поле событий, которые пытаются исследовать ученые, формирующие разные проекты. Одно из таких пересечений – это выводы проекта С.П.Курдюмова («Законы эволюции и самоорганизации сложных систем») и проекта И.Р.Пригожина («Время, хаос, квант»). Но проект И.Р.Пригожина пересекается с еще одной программой: программой поисков так называемых бозонов Хиггса [148,38-45] и программой строительства для этих целей мощного суперколлайдера [69,36-48]. Суть пересечения двух программ следующая. И Пригожин, и физики, ведущие поиск так называемого поля Хиггса и его квантов – бозонов Хиггса, исходят из признания наличия физического вакуума. Но И.Р.Пригожин рассматривает этот феномен для того, чтобы решить космологический парадокс. Физики же, занимающиеся элементарными частицами, имели другие мотивы обращения к вакууму. Их цель – сделать стандартную модель элементарных частиц более совершенной, преодолеть ее неполноту. С этой целью в названную стандартную модель предлагается включить модель бозона Хиггса. С точки зрения физиков-теоретиков, «по-видимому, происхождение масс всех элементарных частиц связано с их взаимодействием с бозоном Хиггса; образно говоря, частицы приобретают массу, «поглощая» бозон Хиггса» [148,38]. И далее: « В настоящее время считают, что в пространстве существует постоянное поле Хиггса (названо так по имени П.Хиггса из Эддинбургского университета – А.С.), т.е. космический вакуум не пустой, а содержит постоянное поле. Поле Хиггса взаимодействует с частицами, порождая их массу… Чем сильнее взаимодействие, тем больше масса» [148,38]. Другими словами, и в космологии, и в стандартной модели элементарных частиц признается феномен вакуума, но обсуждается он по-разному. В стандартной модели элементарных частиц рассматривается только компонент этого вакуума – некое поле Хиггса. В космологии же предлагается феноменологическая модель сущностных граней самого вакуума. Здесь есть смысл снова процитировать фразу И.Р. Пригожина: «Энергия встречается во Вселенной в двух формах. Существует энергия, связанная с гравитацией (соответственно с притяжением), энергия, связанная с массой знаменитой формулой Эйнштейна E=mc2. Энергия, связанная с притяжением, отрицательна (чтобы тело покинуло гравитационное поле другого тела, необходимо затратить энергию), тогда как энергия, связанная с массой, положительна. Отсюда напрашивается вывод, что наша Вселенная, состоящая из массы и энергии, может обладать нулевой общей энергией, как пустая Вселенная – вакуум Минковского» [174,228-229]. Столь обширное да еще повторное цитирование приводится для того, чтобы можно было увидеть аналогии с тем, что пишет Мортинус Дж. Г. Вельтман в упомянутой статье. Он, в частности, подчеркивает, что теоретики «предположили: «истинный» вакуум (т.е. вакуум, в котором нет поля Хиггса) имеет отрицательную кривизну: его космологическая постоянная равна по величине и противоположна по знаку космологической постоянной, порожденной полем Хиггса. Тогда при наличии поля Хиггса пространство должно стать плоским, и Вселенная приобретет знакомые нам черты» [148,41]. Оба эти подхода, конечно, носят феноменологический характер. Это всего лишь рабочие модели, в которых специалисты разных направлений как бы с разных позиций рассматривают предмет и объект своих исследований. И все же очевидно, что разговор идет об одном и том же: о том, как в «исходном», «изначальном»