Минимизация по методу карт Карно

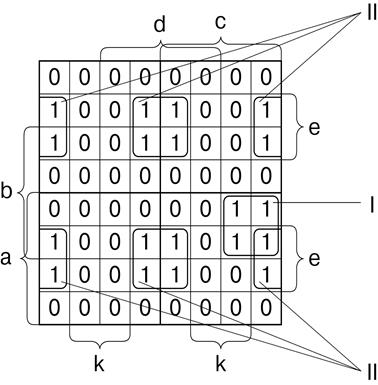
Для проверки правильности минимизации логической функции (1) по первому методу осуществим её минимизацию посредством карт Карно [1, 2]. Преобразованную функцию (2) представим в виде заполненных клеток карты Карно для 6 переменных (рисунок 1), где 1 проставлена в клетках, которые покрываются каким-либо членом минимизируемой функции, в остальных клетках проставляется 0. Затем выделяем «прямоугольные контуры». Количество клеток в контуре должно соответствовать числу 2ⁿ, где n- натуральный ряд чисел, т.е. контур может содержать 1, 2, 4, 8, 16, 32, 64, 128 и т.д. клеток. При этом выделенные контуры должны охватывать все клетки содержащие 1 и отличаться друг от друга хотя бы одной клеткой, т.е. допускается объединение одних и тех же клеток в разные контуры. Необходимо учитывать, что последовательно расположенные клетки одного контура должны отличаться друг от друга только одной переменной, т.е. быть «соседними». Для получения минимального выражения следует стремиться к тому, чтобы количество клеток в контуре было максимально возможным, а количество контуров – минимально возможным, чтобы охватить все 1. При этом рекомендуется учитывать следующее свойство симметричной карты Карно. Отдельные клетки или клетки в контурах, принадлежащие разным элементарным картам (под элементарной понимается карта, содержащая 16 клеток, из них состоят карты Карно для 5 и более переменных), но расположенные симметрично друг другу относительно какой-либо оси (линии), разделяющей элементарные карты, являются «соседними» и, следовательно, могут объединиться в общий контур. Для каждого контура выписываются переменные, которые являются общими для всех его клеток. Эти переменные соединяются между собой знаком логического умножения. Выражения для разных контуров объединяются знаком логического сложения. Карта Карно на рис. 1 содержит два контура. Первый контур охватывает 4 клетки и ему соответствует выражение: 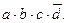Второй контур охватывает 16 клеток и ему соответствует выражение: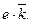

Минимальная функция: 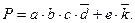Она совпадает с выражением, полученным по методу непосредственного упрощения.

Рисунок 1 –Карта Карно для шести переменных.

3.4 Эквивалентное преобразование логических функций

Эквивалентное преобразование логических функций необходимо для того, чтобы по заданной структурной схеме можно было построить принципиальную логическую схему из имеющегося набора логических элементов. Преобразование осуществляется на основе закона Де Моргана. В контрольной работе необходимо полученное минимизированное выражение представить только из элементарных логических функций: ИЛИ-НЕ (четный вариант), И-НЕ (нечетный вариант) и построить соответствующую преобразованной функции структурную логическую схему.

Эквивалентное преобразование на основе функции ИЛИ-НЕ осуществляется по формулам [1]:

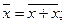
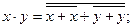
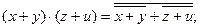
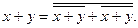
На их основе минимальное выражение заданной логической функции (1) преобразуется к виду:

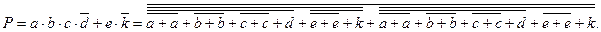(6)

Эквивалентное преобразование на основе функции И-НЕ осуществляется по формулам [1]: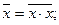

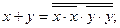
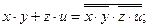
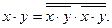
На их основе минимальное выражение заданной логической функции (1) преобразуется к виду:

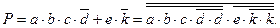(7)