Лекция 8. Соответствия между элементами двух множеств. Определение соответствия между элементами двух множеств. Взаимно однозначные соответствия.

Соответствием между множествами Х и Y называется всякое подмножество произведения этих множеств.

Соответствие можно задавать как любое множество, т.е. либо перечислив все пары элементов, находящихся в данном соответствии, либо указав характеристическое свойство элементов этого подмножества. Например, соответствие между множествами Х = {2, 4, 6, 8} и Y = {3, 5, 7} можно задать:

1) при помощи предложения с двумя переменными: а < b при условии, что а ∈ Х, b∈Y;

2) перечислив пары чисел, принадлежащих подмножеству декартова произведения Х хY: { (2,3), (2,5), (2,7), (4,5), (4,7), (6,7)}. К этому способу задания относят также задание соответствия при помощи графа (рис. 1).

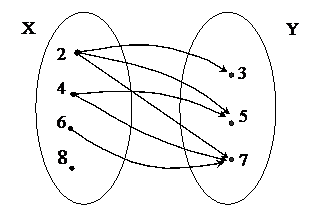
Рис. 1

Соответствие между числовыми множествами можно изобразить при помощи графика в прямоугольной системе координат.

Соответствия принято обозначать буквами P, S, T, R и др. Множество Х называется областью отправления соответствия, а множество Y – областью прибытия соответствия. Если элемент х находится в соответствии R с элементом у , то пишут x R y или ( х , у )∈ R.

Каждому элементу а ∈Х сопоставим подмножество R( а ) в Y, состоящее из всех элементов у∈Y таких, что ( а , у )∈R: R( а ) = { у | ( а , у )∈ R}. Это множество называют образом элемента а при соответствии R.

Каждому элементу b∈Y сопоставим подмножество R ^-1 ( b ) элементов из Х таких, что ( х , b ) ∈ R: R ^-1 ( b ) = { х|( х , b ) ∈R }. Это множество называют полным прообразом элемента b при соответствии R.

Подмножество А⊂Х, состоящее из элементов х , имеющих образы в множестве Y, называют областью определения соответствия R. Подмножество В⊂Y, состоящее из элементов y , имеющих непустые прообразы в множестве Х, называют множеством значений соответствия R.

Пусть S – соответствие между множествами Х и Y. Соответствие S ^-1 между множествами Y и Х называется обратным данному, если у S ^-1 х тогда и только тогда, когда х S у .

Соответствия S и S ^-1 называют взаимно обратными . Граф соответствия S ^-1 получается из графа соответствия S изменением направления всех стрелок.

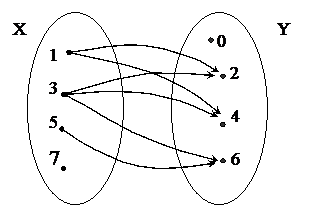рис 2.

П р и м е р 1. Соответствие R между множествами X и Y задано при помощи графа (рис. 2). а) Укажите область отправления, область прибытия, область определения и множество значений соответствия R. б) Задайте это соответствие, перечислением пар чисел. в) Постройте график соответствия R в прямоугольной системе координат. г) Найдите соответствие R ^-1 , обратное данному, и постройте его график.

Р е ш е н и е. а) Из рисунка следует, что областью отправления данного соответствия R является множество Х = {1, 3, 5, 7}, а областью прибытия – множество Y = {0, 2, 4, 6}. Область определения образуют те числа из множества Х, от которых выходит хотя бы одна стрелка, т.е. А = {1, 3, 5}. В множество значений входят те элементы из множества Y, к которым идет хотя бы одна стрелка. Это множество В = {2, 4, 6}.

б) Каждая пара чисел, входящая в данное соответствие, на графе соединена стрелкой, поэтому в виде пар соответствие R можно записать так: {(1,2), (1,4), (3,2), (3,4), (3,6), (5,6)}.

в) График соответствия R в прямоугольной системе координат изображен на рис. 3.

г) Так как граф соответствия R ^-1 получается из графа соответствия R изменением направления стрелок, то соответствие R ^-1 можно получить из соответствия R, поменяв местами компоненты в парах: R ^-1 = {(2,1), (4,1), (2,3), (4,3), (6,3), (6,5)}. График обратного соответствия R ^-1 в прямоугольной системе координат изображен на рис. 4.

П р и м е р 2. Даны два множества: А = {-1, -2, -3, 1, 2, 3, 0}, N – множество натуральных чисел. Поставим в соответствие каждому числу а Î А его квадрат. Выпишите все пары, принадлежащие соответствию. Найдите образ элементов -2 и 0. Найдите полный прообраз 9.

Р е ш е н и е. Найдем множество пар, входящих в данное соответствие: {(-1, 1), (-2, 4), (-3,9), (1, 1), (2, 4), (3, 9)}. Пара (0, 0) в соответствии не присутствует, так как 0 не является натуральным числом. Образом элемента -2 будет число 4 (вторая компонента пары (-2, 4)), число 0 имеет пустой образ. Полным прообразом числа 9 будет множество {-3, 3}.

П р и м е р 3. Соответствие R задано с помощью пар (1, 2), (0, 0), (2, 4), (-1, -2), (-2, -4). Найдите область определения и множество значений этого соответствия. Какой формулой задается это соответствие?

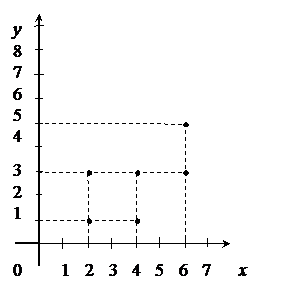
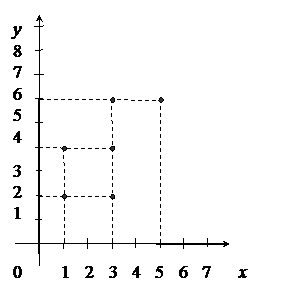Рис. 3 Рис. 4

Р е ш е н и е. В область определения Х входят первые компоненты пар соответствия, поэтому Х = {0, 1, 2, -1, -2}. Множество значений Y соответствия R составляют вторые компоненты пар соответствия, значит, Y = {0, 2, 4, -2, -4}. Замечаем, что вторая компонента в каждой паре получается из первой умножением на число 2, следовательно, данное соответствие можно задать с помощью формулы y = 2 x .

^

Задания для самостоятельной работы по теме 8:

1. Укажите соответствия, существующие между элементами множеств А и В, если: а) А – множество отрезков, В – множество чисел; б) А - множество треугольников, В – множество окружностей.

2. Даны два множества: А = {-1, -2, -3, 1, 2, 3, 0}, N – множество натуральных чисел. Поставим в соответствие каждому числу а∈А его квадрат. Выпишите все пары, принадлежащие соответствию. Найдите образ элементов -2 и 0. Найдите полный прообраз 9.

^