Операции над множествами
Множества. Основные понятия
Понятие множества является основным, неопределяемым понятием, поэтому можно только пояснить этот термин. Под множеством 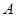 понимается собрание определенных и различимых между собой объектов, мыслимое как единое целое.
понимается собрание определенных и различимых между собой объектов, мыслимое как единое целое.
В этом интуитивном определении, принадлежащем немецкому математику Георгу Кантору (1845-1918), существенным является то обстоятельство, что собрание предметов само рассматривается как один предмет. Что касается самих предметов, которые входя во множество, то относительно них существует значительная свобода. Это может быть и множество целых чисел, и множество точек на плоскости и множество белых носорогов. Множество не обязательно должно содержать в каком-то смысле однородные объекты. Можно объединить в одном множестве и множество объектов и его одиночных представителей. Множества обычно обозначается заглавными латинскими буквами A, B, C,…. Множество можно задать списком, перечислив все его элементы:
При этом порядок, в котором элементы расположены при описании множества, не имеет значения. Не имеет значения также возможность неоднократного повторения одних и тех же элементов при описании множества. | |||
 | |||
| Георг Фердинанд Людвиг Филипп Кантор |
К другому способу задания множества можно отнести порождающую процедуру, например,
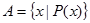 | (1.2) |
В данном случае под выражением 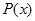 можно понимать арифметические операции, или некоторые неформальные описания.
можно понимать арифметические операции, или некоторые неформальные описания.
Пример. Множество 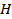 содержит один элемент:
содержит один элемент: 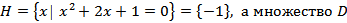 состоит из набора элементов
состоит из набора элементов 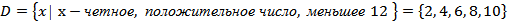 .
.
Определение множества, как совокупности всех неких объектов, которые обладают неким заданным нам свойством, не всегда может привести к однозначному ответу.
Пример Парадокс Рассела. Владелец парикмахерской в одном селе повесил следующее объявление: «Брею тех и только тех жителей села, кто не бреется сам». Спрашивается, кто бреет брадобрея?
Этот парадокс свидетельствует о том, что широко используемая теория множеств в ее интуитивном, «наивном» изложении является противоречивой. Формализация теории множеств, связанная, в частности, с устранением парадоксов, способствовала развитию не только методов теории множеств, но и такой науки, как математическая логика.
Символом 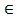 обозначается отношение принадлежности. Запись
обозначается отношение принадлежности. Запись 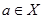 означает, что элемент
означает, что элемент 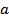 является элементом множества
является элементом множества 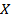 .
.
Определение 1.1. Множества 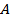 и
и 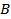 считаются равными, если они состоят из одних и тех же элементов.
считаются равными, если они состоят из одних и тех же элементов.
Записать утверждение о том, что множество 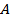 равно множеству
равно множеству 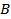 можно при помощи простой формулы
можно при помощи простой формулы
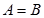 | (1.3) |
Если множества состоят из разных элементов, то этот факт записывают
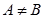 | (1.4) |
ПримерДаны три множества 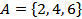 ,
, 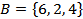 и
и 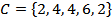 . В силу того, что все три множества состоят из одних и тех же элементов, справедлива запись
. В силу того, что все три множества состоят из одних и тех же элементов, справедлива запись 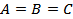 .
.
Пример 1.2.Даны два множества 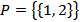 и
и 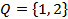 . Эти множества нельзя считать равными, так как единственным элементом множества
. Эти множества нельзя считать равными, так как единственным элементом множества 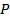 есть множество
есть множество 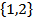 , множество
, множество 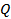 состоит из двух элементов: чисел 1 и 2.
состоит из двух элементов: чисел 1 и 2.
Определение 1.2. Если все элементы множества А принадлежат также множеству В, причем 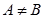 , то множество А является подмножеством В. Этот факт обозначают так:
, то множество А является подмножеством В. Этот факт обозначают так:
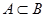 | (1.5) |
Определение 1.3. Если каждый элемент множества А есть элемент множества В, причем возможно 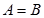 , то множество В включает подмножеством А:
, то множество В включает подмножеством А:
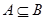 | (1.6) |
Для наглядного представления отношений между подмножествами какого-либо универсального множества используются диаграммы Венна. Простые и лаконичные рисунки, которые впервые предложил английский математик Джон Венн (1834-1923), используются для иллюстрации взаимосвязей и в теории вероятности, и в логике, и в статистике и в информатике. В теории множеств сами множества обозначают областями и размещают внутри прямоугольника, который представляет собой некое универсальное множество 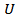 . Если два множества имеют общие элементы, то такие объекты иллюстрируются перекрывающимися областями. . Если два множества имеют общие элементы, то такие объекты иллюстрируются перекрывающимися областями. |  |
| Джон Венн |
Пример 1.5. Даны два множества 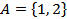 , и , и 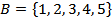 . Для этих множеств справедливо . Для этих множеств справедливо 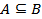 , поскольку множество , поскольку множество 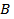 включает множество включает множество 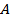 , и каждый элемент множества , и каждый элемент множества 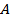 есть элемент множества есть элемент множества 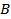 . . | 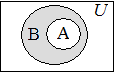 |
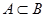 |
Множество, не содержащее элементов, называется пустым, и обозначается символом Ø. Пустое множество есть подмножество любого множества.
Множества бывают конечные и бесконечные. Конечные множества содержат конечное число элементов. Множества, не являющиеся конечными, называются бесконечными.
Число элементов конечного множества называется его мощностью. Мощность множества 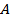 обозначают
обозначают 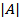 .
.
Пример 1.6. Дано множество 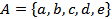 . Тогда
. Тогда 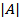 =5.
=5.
Множество всех подмножеств множества 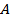 называется множеством-степенью и обозначается
называется множеством-степенью и обозначается 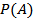 . Если множество
. Если множество 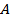 состоит из
состоит из 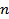 элементов, то множество
элементов, то множество 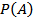 состоит из
состоит из 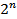 элементов.
элементов.
Пример 1.7. Дано множество 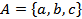 . Множество-степень содержит следующие подмножества:
. Множество-степень содержит следующие подмножества:
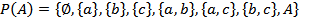
Операции над множествами
Рассмотрим методы получения новых множеств их уже существующих.
Определение 1.4. Пересечением множеств А и В называется множество С , состоящее из всех элементов, одновременно входящих и в множество А, и во множество В. Это записывается следующим образом:
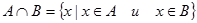 | (1.3) | |
Свойства операции пересечения множеств: 1. 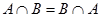 (коммутативность); 2. (коммутативность); 2. 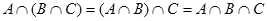 (ассоциативность); 3. (ассоциативность); 3. 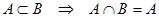 ; 4. ; 4. 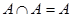 ; 5. ; 5. 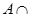 Ø = Ø. Ø = Ø. | 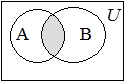 | |
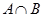 | ||
Пример 1.7. Если множество А есть интервал (1; 5) а множество В есть интервал (2; 7), то пересечение множеств А и В есть интервал (2; 5): 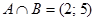 .
.
Определение 1.5. Объединением множеств А и В называется множество С, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из данных множеств или А, или В, или А и В одновременно. Это обозначается следующим образом:
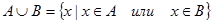 | (1.4) | |
Свойства операции объединения множеств: 1. 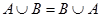 (коммутативность); 2. (коммутативность); 2. 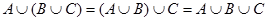 (ассоциативность); 3. (ассоциативность); 3. 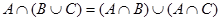 (дистрибутивность); 4. (дистрибутивность); 4. 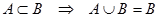 ; 5. ; 5. 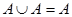 ; 6. ; 6. 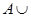 Ø = Ø. Ø = Ø. | 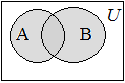 | |
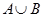 | ||
Пример 1.8. Если множество А есть отрезок [1; 3] а множество В есть отрезок [2; 5], то объединение множеств А и В есть отрезок [1; 5]: 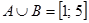 .
.
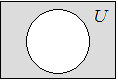
Определение 1.6. Дополнением множества А называется множество всех элементов универсального множества U, каждый из которых не принадлежит множеству А.
Дополнение множества А будем обозначать через 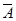
Свойства операции дополнения множеств:
|  |
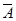 |
Пример 1.9. Если множество А есть отрезок [1; 3], то множество 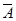 представляет собой объединение двух интервалов:
представляет собой объединение двух интервалов: 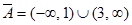 .
.
Определение 1.7. Разностью множеств А и В называется множество С, состоящее из всех элементов, принадлежащих множеству А, но не принадлежащих В:
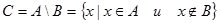 . . | (1.5) |
Операция вычитания множеств не коммутативна: 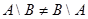 . Из определения разности множеств следует, что имеет место равенство . Из определения разности множеств следует, что имеет место равенство 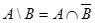 . . | 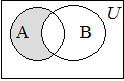 |
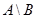 |
Пример 1.10. Если множество А есть отрезок 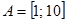 , а множество В есть отрезок
, а множество В есть отрезок 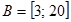 , то разность
, то разность 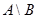 представляет собой полуинтервал
представляет собой полуинтервал 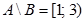 , а
, а 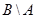 полуинтервал
полуинтервал 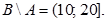 .
.
Определение 1.8. Симметрической разностью множеств А и В называется множество С, состоящее из всех элементов, принадлежащих множествам А и B, но не принадлежащих ихобщим областям.
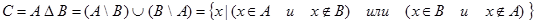 . . | (1.6) |
Другими словами симметрическая разность двух множеств 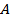 и и 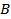 состоит из элементов, которые принадлежат ровно одному из множеств: либо только состоит из элементов, которые принадлежат ровно одному из множеств: либо только 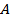 , либо только , либо только 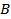 . . | 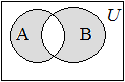 |
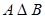 | |
Операция симметрической разности для трех множеств ассоциативна: 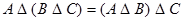 | 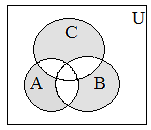 |
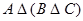 |
Пример 1.11. Если 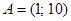 ,
, 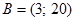 , то
, то 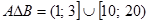 .
.
Определение 1.9. Декартовым произведением двух множеств А и В называется множество С, состоящее из всевозможных пар элементов 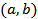 , у которых
, у которых 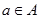 и
и 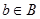 .
.
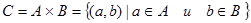 | (1.7) |
Пример 1.12. Даны два множества: 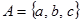 ,
, 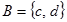 . Для этих множеств можно составить два варианта декартового произведения этих множеств:
. Для этих множеств можно составить два варианта декартового произведения этих множеств: 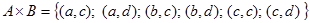 и
и 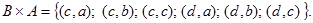
Из примера видно, что множества 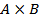 и
и 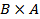 различны.
различны.
Пример 1.13. Пусть множество А есть отрезок 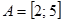 ,на некоторой прямой, а множество В есть отрезок ,на некоторой прямой, а множество В есть отрезок 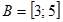 другой прямой. Тогда декартово произведение другой прямой. Тогда декартово произведение 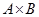 , включающее многочисленные пары координат, составит прямоугольник на плоскости. , включающее многочисленные пары координат, составит прямоугольник на плоскости. | 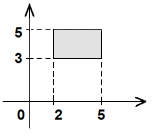 |
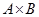 |
Для двух конечных множеств 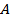 и
и 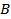 , мощности которых определены как
, мощности которых определены как 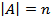 и
и 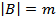 можно вычислить мощность декартового произведения
можно вычислить мощность декартового произведения 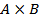 как
как

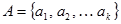
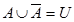 ;
;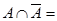 Ø
Ø