Глава 18 модель стабильного населения и ее применение
ОПРЕДЕЛЕНИЕСТАБИЛЬНОГОНАСЕЛЕНИЯ
Модельстационарногонаселения, несмотрянасвоюзначимостьприразработкеотдельныхпонятийирешениицелогоклассапрактическихзадач, какужеотмечалось, вбольшинствеслучаевнесоответствуетдемографическойреальности. Какправило, численностьнаселениятойилиинойстраныизменяется. Этотфактучитываетсявмоделистабильного населения, под которым в демографии понимают теоретическое закрытое население с неизменными во времени возрастными интенсивностями рождаемости, смертности и возрастной структурой населения. Модельстабильногонаселенияявляетсяупрощеннымизображениемпроцессавоспроизводстванаселения. Онастроитсядляодного, главнымобразомдляженскогопола. Параметрымоделидляпротивоположенногополарассчитываютсянаосновесоотношенияполовприрождении.
ОднимизпервыхкидеестабильногонаселенияподошелЛеонардЭйлер (1760). Всвоихисследованияхон, вчастности, обнаружил, чтонаселение, вкоторомустановилсяпостоянныйрежимсмертности, ачислородившихсяизменяетсяпоэкспоненциальномузакону, будетиметьнеизменнуювозрастнуюструктуру. Вначале XX векароссийско-немецкийстатистикВладиславБорткевичиспользовалгипотезустабильногонаселениядляисчислениявозрастногосоставареальногонаселения, численностькоторогоувеличиваетсяспостояннымтемпомприроста. СозданиесобственнотеориистабильногонаселениясматематическимобоснованиемееосновныхположенийсвязаносименемамериканскогодемографаАльфредаЛотки[94]. Именноон, основываясьнааналогиисфизическимипроцессами, ввелвнаучныйобороттермин «стабильноенаселение», чтовпереводеслатинского (от «stabilis») означает «устойчивоенаселение». Еслирежимырождаемостиисмертностистабильногонаселениявнезапноизменятся, азатемвновьвернутсяксвоимпрежнимпостояннымвеличинам, товозрастнаяструктураиобщиедемографическиекоэффициентывэтомнаселениипостепеннотакжевернутсяксвоемуравновесномусостоянию.
СВОЙСТВАЭРГОДИЧНОСТИ
В 1911 годуводнойизпервыхсвоихработЛоткавместесдругимамериканскимученымФ. Шарпом[95]доказалоднуизцентральныхвматематическойдемографиитеорему: закрытое население, в котором возрастныеинтенсивности рождаемости и смертности с определенного моментавремени стали постоянными, со временем будет иметь неизменную возрастную структуру, постоянные общие коэффициенты рождаемости исмертности и коэффициент естественного прироста[96]. Подобноенаселениеназываютасимптотически стабильным, апроцессприближенияегопервоначальнойвозрастнойструктурыиобщихдемографическихкоэффициентовкнекоторымпостоянным (предельным) значениям — стабилизациейнаселения. СамЛоткапользовалсятермином «стабильный» дляобозначенияименнотакогонаселения. Впроцессестабилизациивозрастнаяструктуранаселенияпостепеннокакбы «забывает» своюпервоначальнуюформу. Этоособоесвойствополучилоназваниесильной эргодичности. Послетого, какнаселениедостигнетстабильногосостояния, параметрыеговозрастнойструктурыбудутопределятьсятолькозаданнымирежимамирождаемостиисмертности.
Вконце 1950-хгг. А. Коулвысказалпредположение, чтовсечеловеческиепопуляции «забывают» своепрошлое. Когдауровнирождаемостиисмертностинепрерывноизменяются, такженепрерывноизменяетсявозрастнаяструктуранаселения. Скаждымгодомвлияниеисходнойвозрастнойструктурынаформукаждойпоследующейослабеваетипостепенносходитна «нет». Этосвойстволюбогонаселениясизменяющимисяпараметрамирождаемостиисмертностиудалятьсяотсвоейвозрастнойструктурыдалекогопрошлогополучилоназваниеслабой эргодичности.МатематическионобылодоказаноученикомА. КоулаА. Лопесомвформеследующейтеоремы (теорема Лопеса): если два населения подчиняютсяодинаковым, но изменяющимся во времени режимам рождаемости исмертности, то эти два населения в конце концов приобретут одинаковыевозрастные структуры, хотя конечно эти структуры не обязательностремятся к пределу, как в случае стабильного населения.
Свойстваэргодичностиипроцессстабилизациивозрастныхструктурпредставленынарис. 18.1. Нанемизображенасерияизмененийполовозрастныхпирамиддвухразличныхнасегоднявдемографическомотношениистран — РоссиииЗамбии. Предполагается, чтовэтихстранах, начинаяс 1995 года, установилисьодинаковыережимырождаемостиисмертности. Мывидим, чтовпроцессестабилизацииисходныевозрастныепирамиды: водномслучае — классическаяпирамида, отличающаястранысвысокимуровнемрождаемости, вдругом — пирамида, формакоторойсильнодеформированавойнами, — постепенноразмываются, приобретаясовершенноиныеочертания. Посколькузамбийскоеироссийскоенаселение, поусловию, подчиняютсяодинаковымрежимамрождаемостиисмертности, постолькуихстольнепохожиевначалевозрастныеструктурыстремятсяксовершенноодинаковымпредельнымвозрастнымструктурам. 18.3.ЧИСЛЕННОСТЬ НАСЕЛЕНИЯ, ЧИСЛА РОДИВШИХСЯИ УМЕРШИХ В СТАБИЛЬНОМ НАСЕЛЕНИИ[97]
1. Общие коэффициенты рождаемости и смертности стабильного населения постоянны. Общиекоэффициентырождаемостиnисмертностиmω ω
можновыразитьформуламиn = ∑ fx ⋅cxиm = ∑mx ⋅cx , гдеfxи
x=0 x=0
mx — соответственно, возрастныекоэффициентырождаемости, аcx — долялицввозрастеотxдоx +1 лет. Изпостоянстваэтихвозрастныххарактеристикрождаемости, смертностиивозрастногосостававстабильномнаселениивытекаетпостоянствообщихкоэффициентоврождаемостиисмертности.
2. Коэффициент естественного прироста стабильного населения постоянен. Изравенстваr =n−m , гдеnиm — постоянныевеличины, следуетпостоянствоикоэффициентаестественногоприростаrстабильногонаселения.
3. Стабильное население растет по экспоненциальному закону (илив геометрической прогрессии). Вглаве «Ростнаселения» былопоказано, чточисленностьнаселенияизменяетсяпоэтимзаконам, еслиегокоэффициентприростанеизмененвовремени:
P(t) = P(0)⋅er⋅t . (18.1)
Рис. 18.1. Стабилизация возрастной структуры на примере России (слева)
и Замбии, предполагая, что в обеих странах в течении 100 лет сохраняется режим рождаемости и порядок вымирания, наблюдаемые в России в 1995 г.:TFR =1,344 ,e0муж. = 58,27лет,e0жен. = 71,7лет.
4. Числа родившихсяиумершихвстабильномнаселенииизменяются поэкспоненциальномузакону (иливгеометрическойпрогрессии). ОбозначимчерезP(0) иP(t) — численностьнаселениявмоментывремени 0 иt , черезN(0) иN(t) — соответствующиечислародившихся. ИзпостоянстваобщегокоэффициентарождаемостиможнозаписатьпропорциюNP((tt)) = NP((00)) , азатемвыражениеN(t) = P(t)⋅N(0) P(0). Соотношение (18.1) позволяетнамполучитьискомоеутверждение:
N(t) = N(0)⋅er⋅t . (18.2)
Аналогичнымобразомвыводитсязаконизменениячислаумершихвстабильномнаселении M(t) = M(0)⋅er⋅t , гдеD(0) иD(t) — соответствующиечислаумерших.
18.4.ВОЗРАСТНАЯ СТРУКТУРА СТАБИЛЬНОГО НАСЕЛЕНИЯДоля возрастной группы x в общей численности стабильного населения определяется по формуле c(x) = n⋅l(x)⋅e−r⋅x .Долявозрастнойгруппывточномвозрастеx (иливвозрастеотxдоx + ∆x , где∆x — бесконечномалаявеличина) вобщейчисленностинаселенияопределяетсяпоформулес(x) = P(x,t) P(t) , гдеP(x,t) — численностьлюдейввозрастеxвмоментt .
ФункцияP(x,t) представляетсобойпроизведениечислародившихся xлетназадивероятностиихдожитиядовозрастаx , т.е. P(x,t) = B(t −x)⋅l(x) [98]. Числородившихсяxлетназадравнопроизведениюобщегокоэффициентарождаемостинаобщуючисленностьнаселениявмоментt −x : N(t −x) = n⋅P(t −x).Изсоотношения (18.1) легкополучить, что
P(t −x) = P(t)⋅e−r⋅x . ПослевсехнеобходимыхподстановокполучаемP(x,t) = n⋅P(t)⋅l(x)⋅e−r⋅x . РазделивобечастинаP(t) , мывитогеполучаемматематическоевыражениевозрастнойструктурывстабильномнаселении:
c(x) = n⋅l(x)⋅e−r⋅x . (18.3)
Изформулы (18.3) следует, чтообщийкоэффициентрождаемостира-
венn = c(0) .
Длярасчетовфункциивозрастнойструктурыc(x) стабильногонаселенияследуетиспользоватьдискретноеприближениеформулы (18.3):
c(x,x + τ) ≈ n⋅e−r⋅(x+τ 2) ⋅L(x,x + τ) , (18.5)
гдеx + τ 2 — серединавозрастногоинтервала.
Так, дляпятилетнеговозрастногоинтервалаимеемc(x, x + 5) ≈ n⋅e−r⋅(x+2,5) ⋅L(x,x + 5) .
Вставка 18.1.Пустьнаселениеразбитонаτ -летниевозрастныегруппы. Долякаждойвозрастнойгруппывобщейчисленностинаселениябудетравнасуммевсех возрастоввτ -летнеминтервалеилиинтегралуотxдоx + τ : с 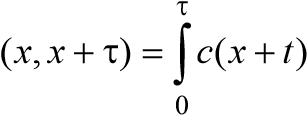 dtили, послеподстановкиформулы (18.3), cdt . (18.4) dtили, послеподстановкиформулы (18.3), cdt . (18.4) 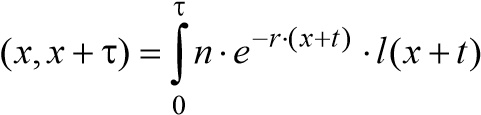 Послерядапреобразованийподынтегральнойфункцииполучаетсярасчетная формула (18.5). Послерядапреобразованийподынтегральнойфункцииполучаетсярасчетная формула (18.5). |
Приr = 0 изформулы (18.4) получаетсявозрастнаяструктурастационарногонаселения: τ
c(x,x + τ) = n⋅∫l(x + t)dt .
Изформулы (18.3) следует, чтовозрастнаяструктуразависитотдвухпеременных: порядкавымиранияl(x) иодногоиздвухвзаимосвязанныхкоэффициентов — общегокоэффициентарождаемостиикоэффициентаестественногоприроста. Приэтом, чем выше, при прочих равных условиях, коэффициент естественного прироста или общий коэффициент рождаемости, тем ниже доля лиц старших возрастов в общей численности населения. Этазависимостьотраженанарис. 18.2. Режимсмертноститрехпопуляций, расположенныхвверхнейчастирисунка, определяетсяфункциейдожитиятиповойтаблицысмертностиООНсожидаемойпродолжительностьюжизниприрождениидлядвухполов, равной 40 лет. Популяцииразличаютсяпокоэффициентамприростанаселения. Видно, чтосамаямолодаявозрастнаяструктуранаблюдаетсяунаселенияснаибольшимкоэффициентоместественногоприроста, равнымr = 2%, самаястарая — устационарногонаселения ( r = 0 ). Аналогичнаязакономерностьнаблюдаетсяутрехнижнихпопуляцийснизкимуровнемсмертности. РежимсмертностивданномслучаезадаетсятиповойтаблицейсмертностиООН сожидаемойпродолжительностьюжизниприрождениидлядвухполов, равной 70 годам. Изрисунка 18.2 видно, чтоприодномитомжеуровнеестественногоприростатепопуляции, гдепродолжительностьжизнивыше, имеютболеенизкуюдолюдетскихиболеевысокуюдолюстаршихвозрастоввобщейчисленностинаселения.
Рис. 18.2. Возрастные пирамиды стабильных популяций с высокой
(e0жен. = 40 ) и низкой (e0жен. = 70 ) смертностью и истинным коэффициентом приростаr = 0%,1%, 2% .
