Показатели отклонений от средней величины: методика расчета и особенности применения

Средняя величина используется для обобщающей характеристики варьирующегося признака совокупности. Это показатель, который одним числом характеризует всю совокупность в целом. Однако для того, чтобы судить о типичности средней для данной совокупности её следует дополнить показателями, характеризующими вариацию величины изучаемого признака. Ведь в ряде случаев ряды распределения, построенные по одному и тому же признаку, могут при одной и той же величине его среднего уровня иметь разную степень вариации этого признака. Покажем на примере:

Количество счетов физических лиц, обслуживаемых филиалами коммерческих банков (тыс. ед.)

Филиалы банков	Банк 1	Банк 2
	6,0	12,4
	2,5	1,5
	5,2	3,2
	5,6	2,0
	9,3	9,5
Итого	28,6	28,6
Средняя	5,7	5,7

Здесь видно, что среднее число обслуживаемых одним филиалом счетов физических лиц в каждом банке одинаковое – 5,7 тыс.ед. Вместе с тем различия (вариация) по количеству обслуживаемых счетов клиентов более резко выражены у филиалов банка 2.

Для измерения степени вариации единиц совокупности по изучаемому признаку используют абсолютные и относительные показатели.

Абсолютные: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.

R – Размах вариации

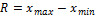
d – среднее линейное отклонение

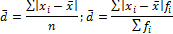
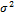– средний квадрат отклонений от средней или дисперсия

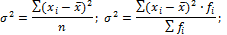
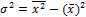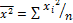А также , где или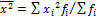

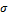- среднее квадратическое отклонение

s w:val="20"/></w:rPr><m:t> </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">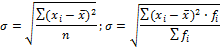

Относительныехарактеристики вариации рассчитываются как отношение абсолютных показателей степени вариации к среднему уровню изучаемого признака. Так относительный размах вариации

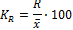
Относительное линейное отклонение

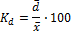
V – коэффициент вариации

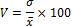
Размах вариации интересен, когда важно знать пределы вариации признака. Например, пределы вариации ставок процента по кредитам и депозитам кредитных организаций одного и того же региона. Или при анализе инвестиционных проектов в условиях риска: из двух проектов тот считается более рискованным, у которого размах вариации экспертной оценки ожидаемого эффекта выше.

В нашем примере у банка 2 размах вариации значительно выше, чем у банка 1: 10,9 тыс. ед. против 6,8 тыс. ед Очевидно, что деловая активность банка два складывалась под влиянием более разнообразных условий. Следовательно, возникает вопрос, насколько точно рассчитанная для филиалов банка 2 средняя величина обслуживаемых счетов клиентов характеризует его индивидуальный уровень отдельных филиалов., т.е. вопрос о типичности средней. Однако характеристика вариации только с помощью размаха недостаточна, так как величина этого показателя зависит от значений только двух крайних вариант признака. Для обобщения всех величин признака в изучаемой совокупности используют показатели среднего линейного и среднего квадратического отклонений, которые имеют те же единицы измерений, что и варианты признака. В формуле среднего линейного отклонения стоит модуль, так как по свойству средней сумма отклонений от средней равна нулю, а если поставить модуль то мы можем охарактеризовать вариацию признака в совокупности. Однако более широкое применение получило среднее квадратическое отклонение.

Дисперсию и среднее квадратическое отклонение используют при расчетах, связанных с организацией выборочного наблюдения, оценке полученных на основе выборки статистических показателей и т.д.