Статистическое изучение вариации в рядах распределения

Вариацией признака называется различие численных значений признака у отдельных единиц совокупности. Размеры вариации позволяют судить, насколько однородна изучаемая группа и, следовательно, насколько характерна средняя по группе. Изучение отклонений от средних имеет большое практическое и теоретическое значение, так как в отклонениях проявляется развитие явления.

Статистические данные представлены в рядах распределения. В зависимости от признака, положенного в основу группировки данных, различают атрибутивные и вариационные ряды. Числовые значения признака, встречающееся в данной совокупности называется вариантами значений. Статистические данные без какой-либо систематизации образуют первичный ряд.

Пример.

№ ТЭЦ
Себестоимость 1 кВт.ч, тыс. руб.	5,8	6,6	5,9	6,7	6,6

При наличии достаточно большого количества вариантов значений признака для его изучения необходимо упорядочения первичный ряд, т.е. проранжировать – расположить все варианты ряда в возрастающем (или убывающем) порядке.

№ ТЭЦ
Себестоимость 1 кВт.ч, тыс. руб.	5,8	5,9	6,6	6,6	6,7

При рассмотрении ранжированных данных можно увидеть, что варианты значений признака у отдельных единиц повторяются. Число повторений отдельных вариантов называют частотой повторения ( ).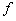

По характеру вариации различают дискретные и непрерывные признаки. Дискретные признаки отличаются друг от друга на некоторое прерывное число.

Таблица 16

Распределение рабочих цеха по квалификации

Тарифный разряд ( 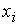)	Число рабочих 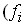)	Частости ( 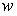)	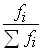Накопленные частоты (Fi)
II		0,05
III		0,25
IV		0,40
V		0,20
VI		0,10
Итого:		1,00

Вместо абсолютного числа рабочих, имеющих определенный разряд, можно установить долю рабочих этого разряда. Частоты, представленные в относительном выражении, называют частостями и обозначают :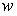

.

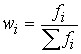Частости могут быть выражены в долях единицы или в процентах. Накопленные частоты определяют последовательным суммированием частот.

Непрерывные признаки могут отличаться один от другого на сколь угодно малую величину и в определенных границах принимать любые значения. Для построения ряда распределения непрерывных признаков, значения вариантов указываются в интервалах «от – до». При построении интервальных рядов необходимо определить число интервалов и определить величину интервала:

.

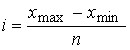Если вариационный ряд дан в неравных интервалах, то для правильного представления о характере распределения необходимо рассчитать абсолютную и относительную плотности распределения. Абсолютная плотность:

,

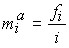где 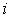– величина интервала.

Относительная плотность:

,

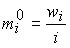где 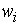– частость.

Эти показатели используют для преобразования интервалов, если данные собраны по различным совокупностям и по разному обработаны:

.

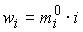Для характеристики размера вариации используются специальные показатели колеблемости: размах вариации, средне линейное отклонение, среднее квадратическое отклонение, коэффициент вариации.

Размах вариации – величина разности между максимальным и минимальным значениями признака:

.

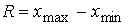Достоинством этого показателя является простота расчета. Недостаток заключается в том, что данный показатель опирается только на два крайних значения признака и не учитывает степени колеблемости основной массы членов ряда.

Среднее линейное отклонение – это средняя арифметическая из абсолютных отклонений индивидуальных значений признака от среднего значения.

Для первичного ряда: .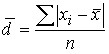

Для ряда распределения: .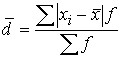

Так как согласно свойству средней арифметической алгебраическая сумма отклонений индивидуальных значений признака от средней арифметической равна нулю, то для расчета 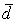суммируются абсолютные значения индивидуальных отклонений независимо от знака.

Среднее линейное отклонение показывает, насколько в среднем отличаются индивидуальные значения признака от среднего их значения.

Среднее квадратическое отклонение равно квадратному корню из среднего квадрата отклонений индивидуальных значений признака от средней арифметической.

Для первичного ряда: .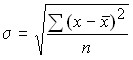

Для ряда распределения: .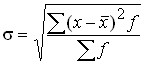

Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем колеблется величина признака у единиц изучаемой совокупности: 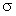> 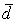. Для умеренно асимметричных рядов распределения установлено следующее соотношение: 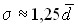или .

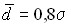Дисперсия имеет самостоятельное значение в статистике и относится к числу важнейших показателей:

Для первичного ряда: .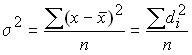

Для вариационного ряда: .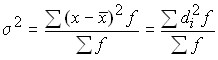

Следовательно: .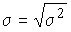

В статистике часто возникает необходимость сравнения вариации различных признаков. В таких случаях используют показатель относительного рассеяния – коэффициент вариации:

.

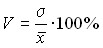Коэффициент вариации показывает, на сколько процентов в среднем индивидуальные значения отличаются от средней арифметической. Он является критерием надежности средней: если он превышает 40%, то это свидетельствует о большой колеблемости признака и, следовательно, средняя недостаточно надежна.

Линейный коэффициент вариации: .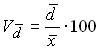

Коэффициент осцилляции: .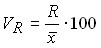

Дисперсия обладает рядом свойств.

1. Дисперсия постоянного числа равна нулю. Если 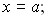то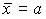

.

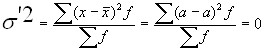2. Если все варианты одного ряда увеличить или уменьшить на какое-либо число, то дисперсия нового ряда не изменится.

Пусть 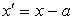, но тогда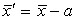

.

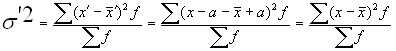3. Если все варианты ряда уменьшить или увеличить в 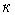раз, то дисперсия нового ряда уменьшится (или увеличится) в .

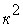Пусть 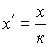, тогда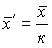

.

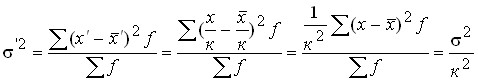Моментом распределения называется средняя арифметическая тех или иных степеней отклонений индивидуальных значений признака от определенной исходной величины. В общем виде момент можно записать следующим образом:

,

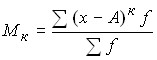где А – величина, от которой определяются отклонения;

к – степень отклонения (порядок момента).

В зависимости от величины к моменты могут быть рассчитаны любого порядка, но практическое применение находят моменты первых четырех порядков.

В качестве постоянной величины А может быть принято любое число. В зависимости от того, что принимается за постоянную величину, различают следующие три вида моментов:

1) если в качестве постоянной величины принят нуль, т.е. А = 0, то моменты именуют начальными. В общем виде их можно записать:

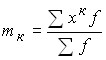и соответственно моменты первых четырех порядков;
;
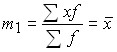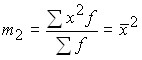– средняя арифметическая из квадратов вариантов;
;
.

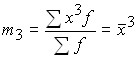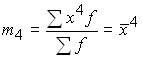2) если в качестве постоянной величины принята средняя арифметическая ряда, т.е. А = 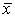, то моменты именуют центральными:

;
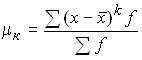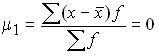согласно свойству средней арифметической;
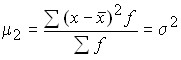дисперсия;
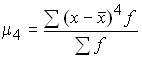для расчета показателя эксцесса.

3) если в качестве постоянной величины принято любое число, отличное от нуля, то момент именуют условным:

;
;
;
;
.

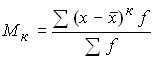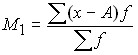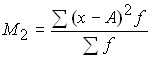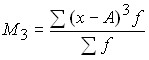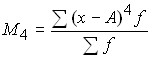Используя начальные моменты первого и второго порядка можно получить формулу для расчета дисперсии:

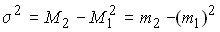
Вычислить дисперсию можно также следующим образом:

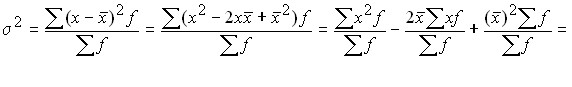
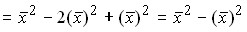
Следовательно, дисперсия может быть определена как разность среднего квадрата вариантов и квадрата их средней.

В вариационных рядах с равными интервалами дисперсия может быть вычислена способом моментов и способом отсчета от условного нуля.

Расчет производится по формуле:

,

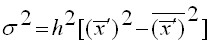где:

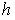- ширина интервала;
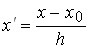, х0 – условный нуль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
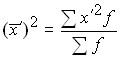– момент второго порядка;
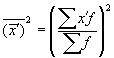– квадрат момента первого порядка.

Единицы изучаемых явлений могут характеризоваться такими признаками, которыми одни единицы совокупности обладают, а другие – нет. Такой признак называется альтернативным.

Наличие признака обозначается единицей, а его отсутствие – нулем. Доля единиц, обладающих этим признаком, обозначается p, а доля, им не обладающая – q. Следовательно, p + q = 1, q = 1 – p. Среднее значение альтернативного признака равно:

.

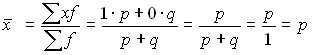Таким образом, среднее значение альтернативного признака равно величине той доли единиц, которая им обладает.

Определим дисперсию:

.
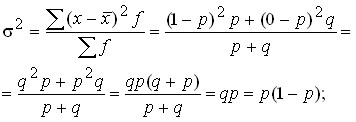
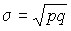