Сущность средних величин и их значение в статистическом анализе.

Теория статистики

1. Понятие статистики. Предмет и метод статистики.

Статистика – практическая деятельность по сбору, накоплению, обработке и анализу цифровых данных, характеризующих население, культуру, политику и другие сферы общественной жизни.

Статистика – это наука, изучающая количественную сторону явлений в жизни общества. Наука и практика тесно взаимосвязаны. Наука основываясь на практических данных разрабатывает методы проведения статистических исследований. Практика не использует эти методы в решениях задач.

Предмет статистики это массовые общественные явления и процессы, а также закономерности их развития. Статистика изучает влияние природных и технических факторов на изменение количественных характеристик социально-экономических явлений и влияние жизнедеятельности человека и общества на среду.

Явления и процессы изучаются с помощью статистических показателей.

Статистическийпоказатель – количественная оценка свойства, изучаемого явления.

Изучая предмет статистики выявляется статистическая совокупность, т.е. множество единиц изучаемого явления, объединенных в соответствии с задачей исследования единой качественной основы.

Основным методом является диалектический, т.е. все явления и процессы, происходящие в жизни общества рассматриваются во взаимосвязи и развитии (динамике). К методам относятся:

1. Метод массовых статистических наблюдений.

Статистическое наблюдение заключается в сборе первич­ного статистического материала, в научно организованной регистрации всех существенных фактов, относящихся к рассмат­риваемому объекту. Это первый этап всякого статистического исследования.

2. Группировочный метод.

Метод группировок дает возможность все собранные в результате массового статистического наблюдения факты подвергать систематизации и классификации. Это второй этап статистического исследования.

3. Метод обобщающих статистических показателей.

Метод обобщающих показателей позволяет харак­теризовать изучаемые явления и процессы при помощи статистических величин —абсолютных, относительных и средних. На этом этапе статистического исследования выявляются взаимосвязи и масштабы явлений, определяются законо­мерности их развития, даются прогнозные оценки. - абсолютных; –относительных; –средних

4. Математические методы.

Математи́ческая стати́стика — наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.

Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала (напр., оценить необходимый объём выборки для получения результатов требуемой точности при выборочном обследовании).

1. Понятие метода массовых статистических наблюдений. Организационные формы и виды статистических наблюдений. Виды ошибок статистических наблюдений.

Статистическое наблюдение - это предварительная стадия статистического исследования, которая представляет собой планомерный, научно организованный учет (сбор) первичных статистических данных о массовых социально-экономических явлениях и процессах.

Статистическое наблюдение (сбор первичного статистического материала) состоит из трех основных этапов:

1. подготовка статистического наблюдения;

2. организация и производство наблюдения;

3. контроль полученных первичных данных.

Программой наблюдения называют перечень вопросов, которые подлежат регистрации при проведении наблюдения. Чтобы программа наблюдения была научно обоснована и правильно составлена, к ней предъявляются следующие требования:

- четкая и конкретная формулировка главной цели наблюдения;

- определение места и времени наблюдения, где определяются критический момент (дата или интервал времени, по состоянию на который проводится регистрация признаков) и срок (период заполнения статистического формуляра);

- выделение ряда наиболее существенных признаков объекта наблюдения;

- комплексное определение типа, основных черт и свойств изучаемого явления;

- вопросы, сформулированные в программе, не должны носить двусмысленный характер;

- соблюдение логического принципа последовательности вопросов;

- включение в программу вопросов контрольного характера для проверки собираемых статистических данных;

- сочетание закрытых и открытых вопросов программы.

На втором этапе решаются важнейшие организационные вопросы статистического наблюдения. Они заключаются в том, чтобы выбрать соответствующие целям и задачам конкретного статистического наблюдения организационные формы наблюдения, виды наблюдения и способы получения статистической информации.

По видам статистического наблюдения:

а) по времени регистрации фактов.

б) по охвату единиц совокупности.

По способам получения статистической информации:

- непосредственное наблюдение; когда можно установить факт, подлежащий регистрации.

- документальный способ; основанный на использовании в качестве источника информации различных документов учетного характера (счета, рекламации и т.д.) и способствующий получению точной информации.

- опрос - экспедиционный, Устный опрос может быть как прямым (непосредственное общение счетчика с респондентом), так опосредованным (например, по телефону).

- анкетный, определенное число респондентов получают специальные вопросники либо лично, либо через средства печати. Данный вид опроса применяется в исследованиях, где нужны ориентировочные результаты, не претендующие на высокую точность (изучение общественного мнения).

- явочный; используется в сплошном наблюдении, когда необходимо личное присутствие (регистрация браков, разводов, рождений и т.д.).

- корреспондентский, сведения сообщаются штатом добровольных корреспондентов, в силу чего полученный материал не всегда носит качественный характер.

- саморегистрация. формуляры заполняются самими респондентами, а счетчики консультируют и собирают формуляры. В статистической практике различные виды статистических наблюдений могут сочетаться, дополняя друг друга.

Основной формой статистического наблюдения является отчетность. Если первичный учет (первичный учетный документ) регистрирует различные факты, то отчетность является обобщением первичного учета.

Отчетность - официальный документ, который скрепляется подписями лиц, ответственных за предоставление и достоверность собранных сведений, и утверждается органами государственной статистики.

К специально организованному статистическому наблюдению можно отнести перепись. Перепись - наблюдение, повторяющееся через равные промежутки времени, задачей которого является не только определение численности и состава исследуемой совокупности, но и анализ количественных изменений в период между двумя обследованиями.

Формой непрерывного статистического наблюдения является регистровое наблюдение (регистр), объектами которого являются долговременные процессы, имеющие фиксированное начало, стадию развития и фиксированное время завершения.

Регистр основан на системе отслеживания состояния переменных и постоянных показателей. В статистической практике различают регистры населения и регистры предприятий.

Виды статистического наблюдения по времени регистрации фактов.

Непрерывное (текущее) статистическое наблюдение - это систематическая регистрация фактов или явлений по мере их поступления с целью изучения их динамики.

Видами прерывного наблюдения являются единовременное и периодическое. Первое есть разовое сплошное наблюдение для сбора количественных характеристик явления или процесса в момент его исследования. Периодическое наблюдение проводится через определенные промежутки времени по схожим программе и инструментарию.

По охвату единиц совокупности статистическое наблюдение бывает сплошным и несплошным.

Сплошное наблюдение охватывает все единицы исследуемой совокупности (например, общая перепись населения).

В свою очередь, несплошное наблюдение охватывает только часть исследуемой совокупности. В зависимости от того, как выбрана эта часть, несплошное наблюдение можно подразделить на выборочное (основано на принципе случайного отбора), метод основного массива (исследуются самые существенные или наиболее крупные единицы изучаемой совокупности) и так называемое монографическое наблюдение (подробное исследование отдельных единиц изучаемой совокупности с целью выявления намечающихся тенденций).

На третьем этапе собранный статистический материал должен пройти контроль. Целью этого этапа является как счетный, так и логический контроль полученных первичных данных. Расхождение между расчетным и действительным значениями исследуемой величины в статистике называют ошибкой наблюдения. В зависимости от причин возникновения различают ошибки регистрации и ошибки репрезентативности.

Ошибки регистрации могут быть случайными и систематическими. Случайные ошибки не имеют определенной направленности и возникают под действием случайных факторов. При обобщении массового материала эти ошибки взаимопогашаются.

Систематические ошибки регистрации имеют определенную направленность, могут либо завышать, либо занижать конкретное значение показателя, что в итоге приводит к искажению действительного положения.

Для выявления ошибок используется счетный контроль, особенно для проверки итоговых сумм. Помимо счетного используется и логический контроль, который может поставить под сомнение правильность полученных данных, поскольку основан на логической взаимосвязи между признаками.

Если ошибки регистрации свойственны любому наблюдению (сплошному и несплошному), то ошибки репрезентативности - только несплошному наблюдению. Они характеризуют расхождения между значениями показателя, полученного в обследуемой совокупности, и его значением по исходной (генеральной) совокупности. Ошибки репрезентативности также могут быть случайными и систематическими. Случайные ошибки возникают, если отобранная совокупность не полностью воспроизводит все признаки генеральной совокупности и величину этих ошибок можно оценить. Систематические ошибки репрезентативности могут возникать, если нарушен сам принцип отбора единиц из исходной совокупности. Контрольной проверкой собранных данных завершается статистическое наблюдение.

3. Понятие группировки и ее виды. Ряды распределения. Полигон и гистограмма.

Статистическая сводка – систематизация единичных фактов, позволяющая перейти к обобщающим показателям изучаемой совокупности и ее частям, а также осуществить анализ и прогнозирование изучаемых явлений и процессов.

Различают сводку в широком и узком смысле слова.

Сводка в узком смысле слова, т.е. в простом представляет собой ранжирование, т.е. упорядочение в порядке возрастания или убывания данных, а также суммирование по всем единицам наблюдения.

Сводка в широком смысле предполагает разделение на качественно однородные группы, для характеристики этих групп по ряду существенных признаков. Элементами сводки в широком смысле являются:

1. Программа сводки;

2. Исчисление обобщающих показателей по каждой группе и по всей совокупности в целом;

3. Оформление конечных результатов сводки в статистические таблицы или графики.

Группировка – объединение единицы совокупности в качественно однородные группы для изучения структуры совокупности, связи между признаками для характеристики различных типов изучаемых явлений.

Всякая группировка имеет основной группировочный признак – факторный, который служит основанием для распределения признаков по группам, а для характеристики по взаимосвязи между отдельными явлениями и процессами добавляются значения результативного признака, который зависит от факторного.

От цели экономического анализа и от исходной информации – группировки делят:

- Аналитические; имеют количественно выраженный признак.

- Типологические; признак не имеет количественного значения, а означает какое-то понятие, т.е. тип.

- Структурные; исследуют цель определения структуры изучаемого явления и помогают выявить соответствие входящих в изучаемую совокупность составных частей

- Комбинированные; Различное сочетание первых трех видов.

-Территориальные. Группировка по географическому признаку.

Результаты сводки и группировки материалов статистического наблюдения оформляются в виде рядов распределения и таблиц. Статистические ряды распределения представляют собой упорядоченное расположение единиц совокупности по группам и группировкам.

Ряды распределения изучают структуру совокупности, позволяют изучить ее однородность, размах и границы. Ряды распределения, образованные по качественным признакам, называют атрибутивные(заработная плата, объем товарооборота). При группировке по количественному признаку выделяются вариационные.

Вариационные ряды по строению бывают:

1. Дискретными (прерывными) – основанные на прерывных вариациях признака (2 кассы, 3 отдела).

2. Интервальные (непрерывные) – имеющие любые, в том числе и дробные количественные выражения (стаж работы от 5 до 10 лет).

- с равными интервалами

- с неравными интервалами

При построении вариационных рядов пользуются понятиями:

1. Варианта (x); Варианта – отдельное значение варьируемого признака, которое он принимает в ряду распределения.

2. Частота (f); Частота – численность отдельных вариант или каждой группы вариационного ряда. Частоты, выраженные в % или долях процента называются частостями.

3. Частость. Накопленная частота.

В практике экономической работы возникает потребность в преобразовании рядов распределения в куммулятивные ряды, строящиеся по накопленным частотам. Накопленные частоты определяются путем последовательного прибавления к частотам I группы показателей последующих групп ряда распределения. Комуляту часто изображают графически . С помощью комулятивных кривых можно изображать процесс концентрации. Если варианта ряда распределения имеет незначительные колебания и распределение носит довольно равномерный характер, то при построении рядов распределения используют равновеликие интервалы, которые определяются по формуле:

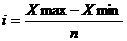; R= xmax - xmin – Размах вариации.

где Xmax и Xmin – наибольшие и наименьшие значения вариант в ряду;

n – число групп;

разность (Xmax – Xmin) – размах вариации;

i – равновеликий интервал. (шаг)

Если совокупность больше 100 единиц для определения оптимального количества групп рекомендуется использовать формулу Стерджесса:

n=1+3,322lgN , где N – количество единиц в совокупности.

Интервальный вариационный ряд изображается при помощи гистограммы. Где по оси ох откладывается признак, а по оси оу - частота.

Гистограмма может быть преобразована в полигон распределения.

Полигон частот образуется ломаной линией, соединяющей точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов, срединные значения откладываются по оси х, а частоты – по оси у.

Из сравнения двух рассмотренных способов графического представления эмпирических распределений следует, что для получения полигона частот из построенной гистограммы нужно середины вершин прямоугольников, образующих гистограмму, соединить отрезками прямых.

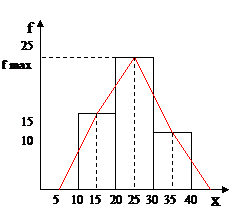
График изображения полигона на гистограмме.

Дискретный вариационный ряд тоже может быть показан на полигоне, только точки построения это не средние величины интервалов, а конкретное значение.

4. Абсолютные статистические показатели.

В итоге статистической сводки образуются обобщающие показатели, характеризующие результаты познания количественной стороны общественных явлений. К таким показателям относят абсолютные, относительные и средние величины. Абсолютные величины бывают двух видов

1. индивидуальные;

2. суммарные.

Индивидуальные характеризуют размеры отдельных единиц совокупности. Индивидуальные абсолютные величины получают в результате статистического наблюдения и фиксируют в первичных документах.

Суммарные абсолютные величины определяют путем суммирования отдельных индивидуальных величин.

Абсолютные величины отражают естественную основу явлений, они выражаются либо численностью единиц совокупности, либо в их абсолютных размерах в натуральных единицах, вытекающих из физических свойств. Абсолютные величины измеряются в следующих единицах измерения:

1. натуральных (тонны, кг., гр., шт.);

2. в трудовых (часы, дни, месяца, человеко-часы, человеко-дни);

3. стоимостные (руб., млн. руб.);

4. комбинированные (тон. км., цент/га.).

При определении суммарных показателей, когда индивидуальные величины характеризуют отдельные разновидности продукции, близкие по своим свойствам, применяются условные натуральные измерители.

При определении абсолютных показателей их могут сравнивать, при этом рассчитывая абсолютные отклонения.

5. Относительные статистические показатели.

Одной из наиболее распространенных обобщающих величин в статистике является относительная величина.

Относительные величины представляют собой меру количественного соотношения конкретных явлений в общественной жизни.

Относительная величина рассчитывается как отношение двух взаимосвязанных показателей. При этом в числителе находится сравниваемая величина, а знаменатель содержит базу относительного сравнения. Если база сравнения принята за единицу, то рассчитываемый показатель называется коэффициент. Если база сравнения принята за сто, то называется процент. Если база принимается за тысячу, то исчисляемая величина называется промилей. Если за десять тысяч, то продецемилей. Относительные величины бывают следующих видов:

1. Процент выполнения плана: факт/план 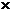100%

2. Относительная величина структуры – характеризует долю отдельных частей в общей совокупности. Относительные величины структуры называют удельным весом единиц в общей совокупности. 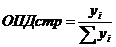, где i – число частей целого.

3. Относительные величины динамики, они характеризуют изменения явлений во времени по сравнению с уровнем, принятым за базу сравнения.

Относительные величины динамики принято называть темпами роста (Т).

Цепные темпы роста ; ; ;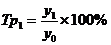

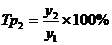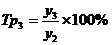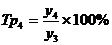
Базисные темпы роста - за основу принимается постоянная база сравнения, т.е. начальный уровень ряда динамики.

; ; ;

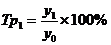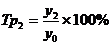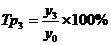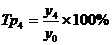
4. Относительные величины координации, характеризующие отношения отдельных частей совокупности с одной из них, принятой за базу сравнения (численность сел. жителей на 100 человек городских жителей). 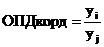, где i,j – число частей одного целого.

5. Относительные величины интенсивности – показатели, характеризующие меру распространения или развития данного явления в определенной среде, они рассчитываются как отношение абсолютной величины к размеру среды, в которой они находятся.

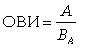, где А – степень распространение явления; ВА - среда распространения явления А.

6. Относительная величина планового задания (ОВПЗ) используется для расчета в процентном отношении увеличения (уменьшения) величины показателя плана по сравнению с его базовым уровнем в предшествующем периоде, для чего используется формула

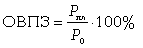
7. Относительные величины сравнения, получаются путем сравнения одноименных уровней, относящихся к разным объектам, территориям за один и тот же период или на один и тот же момент времени.

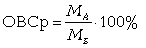, где МА - показатель первого одноименного исследуемого объекта; МБ - показатель второго одноименного исследуемого объекта (база сравнения).

6. Средние величины: степенные и структурные. Виды средних степенных (арифметическая, геометрическая, квадратическая, гармоническая, простая и взвешенная). Правило мажорантности.

Свойства дисперсии.

Если из всех значений вариант вычесть какое-то постоянное число, то средний квадрат отклонений не изменится:

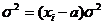
Если все значения вариант разделить на какое-то постоянное число, то средний квадрат отклонений уменьшиться в а раз:

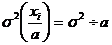
Если средний квадрат отклонений от любой величины а – которая отличается от средней арифметической х, то он будет всегда больше среднего квадрата отклонений от средней арифметической: 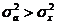, но больше на определенную величину, а эта величина определена, как квадрат разности между средней и этой, условно взятой величиной:

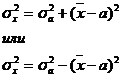
используя 2-ое свойство дисперсии в математической статистике можно рассчитать дисперсию способом моментов. Средний квадрат отклонений от средней величины имеет свойства min, т.е. дисперсия от средней всегда меньше дисперсий исчисляемых от других величин. В этом случае, если а – постоянное число = 0, то, следовательно, средний квадрат отклонений будет определяться по формуле:

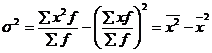
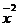- ср. квадрат значений признака;

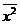- квадрат среднего значения признака.

Значит, средний квадрат отклонений 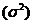равен разности между средним квадратом значения признака и квадратом ср. значения признака.

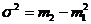
Также способ моментов называется способом отсчета от условного нуля. Данный способ можно применять только в тех случаях, если в вариационных интервальных рядах интервалы одинаковы.

Используя 2-ое свойство дисперсии, разделив все варианты на величину интервала, получим формулу дисперсии:

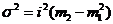где i – величина интервала для данной совокупности ;

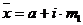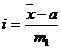
Рис. 5. Кривая нормального распределения

Выравнивание фактического распределения по кривой нормального распределения.

Cостоит из нескольких этапов:

сравнивают фактические и теоретические частоты. По фактическим данным определяют теоретические частоты кривой нормального распределения, которая является функцией нормированного отклонения;

проверяют на сколько распределение признака соответствует нормальному.

Критерии согласия.

Математическая статистика дает несколько показателей, по которым можно судить, на сколько фактическое распределение согласуется с нормальным. Эти показатели называются критериисогласия.

Критерий согласия Колмагорова (критерий 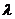) определяется путем деления max разности коммулятивных частот на корень квадратный из числа наблюдений:

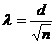, где d – максимальное отклонение фактической частоты от фактической частоты;

n – число наблюдений.

По специальной таблице вероятности для критерия согласия 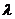определяют, что значение 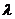=0,59 соответствует вероятности 0,88. Это значит, что с вероятностью 0,88 можно судить об отклонении фактических частот от теоретических, которые являются случайными.

Корреляционный анализ

Различают:

- парную корреляцию – это зависимость между результативным и факторным признаком;

- частную корреляцию – это зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков;

- множественную – многофакторное влияние в статической модели .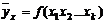

К простейшим показателям тесноты связи относятся:

- линейный коэффициент корреляции Пирсона;

- коэффициент детерминации;

коэффициенты корреляции знаков – для оценки тесноты связи качественных признаков (непараметрические методы), Г. Фехнера, К. Спирмэна, М. Кэндэла.

Коэффициент Фехнера (коэффициент корреляции знаков).

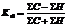, Как и любой показатель тесноты связи коэффициент Фехнера может принимать значения от –1 до +1 ( 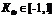). Если ΣН=0, знаки всех отклонений совпадают и К_ф = 1. Если ΣС=0, знаки всех отклонений не совпадают и К_ф = 0.

Линейный коэффициент корреляциипредставляет собой среднюю величину из произведений нормированных отклонений для х и у: 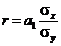, где a₁ – коэффициент регрессии в уравнении связи. Линейный коэффициент корреляции может принимать
значения от –1 до +1 ( 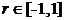) Оценка линейного коэффициента корреляции

Значение r	Характер связи	Интерпретация связи
r = 0	Отсутствует	Изменение x не влияет на изменения y
0 < r < 1	Прямая	С увеличением x увеличивается y
–1 > r > 0	Обратная	С увеличением x уменьшается y и наоборот
r = 1	Функциональная	Каждому значению факторного признака строго соответствует одно значение результативного

Определяется расчетное значение t-критерия Стьюдента:

,

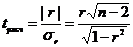Регрессионный анализ

Парная регрессия

линейная 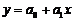. полулогарифмическая ;

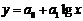показательная 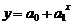; степенная ;

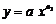параболическая 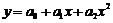; гиперболическая .

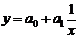Для оценки параметров уравнений регрессии наиболее часто применяют метод наименьших квадратов (МНК)суть которого (для линейной зависимости):

Отсюда можно выразить коэффициенты регрессии:

; .

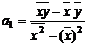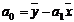Коэффициент регрессии а₀ иногда называют константой уравнения связи.

Коэффициент эластичности Э

.

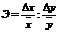Для линейной регрессии .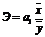

Более точно коэффициент эластичности определяют ,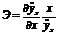

где 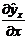– первая производная уравнения регрессии у по х. Для линейной зависимости , .

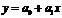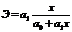Множественная регрессия

Линейное уравнение множественной регрессии

.

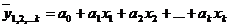Система нормальных линейных уравнений МНК для оценки коэффициентов двухфакторной регрессии 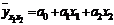имеет вид:

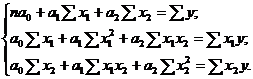
Классификация индексов.

Индексы классифицируются по ряду признаков:

1. В зависимости от объектов исследования:

индексы объема (структуры);

качественные индексы (индексы цены, себестоимости).

2. По охвату:

индивидуальные индексы;

общие индексы;

групповые индексы.

Индивидуальныеиндексы – дают сравнительную характеристику отдельных элементов совокупности (индекс физического объема, себестоимости, производительности и т.д.).

Обозначается i.

Общие индексы – характеризуют изменение совокупности в целом, обозначают J.

Групповые индексы – охватывают не все элементы совокупности, а только отдельные части.

Групповые индексы рассчитывают с помощью метода группировок, собирая и группируя данные за период.

3. В зависимости от методологии расчета общие и групповые индексы делят на:

агрегатные;

средние из индивидуальных.

Прикладная статистика

Статистика населения

21. Понятие Населения. Среднегодовая численность населения.

Основные показатели численности населения и методика их расчета

Для развития национальной экономики в целом и для развития ее основных отраслей необходима статистическая информация о населении. Как статистическая категория население представляет собой совокупность людей, проживающих на данной территории. Оно непрерывно изменяется за счет рождения и смертей.

Информация о населении включает его естественный прирост, его естественное движение, его профессиональный состав, возрастной состав, численность трудоспособного населения. Единицей наблюдения или единицей учета в статистике населения может быть как отдельный человек, так и семья, а также домохозяйство и населенный пункт.

Основным источником информации о населении является текущий учет (сплошная перепись) населения, который, как правило, проводится раз в десять лет. Отдельные сведения собираются на основе выборочной переписи населения. При переписи населения учитываются две категории населения: наличное население(лица, фактически находящиеся на момент переписи в данном населенном пункте, включая временно проживающих) и постоянное население (лица, для которых данный населенный пункт является местом постоянного проживания, включая временно отсутствующих).

В ходе статистического обследования населения определяется численность населения на момент проведения переписи. Сведения о наличном населении очень важны для населенных пунктов, где сильно влияние сезонного фактора (курортные районы) или для поселков, где используется рабочая сила вахтовым методом.

По результатам переписи исчисляется такой показатель, как среднегодовая численность населения, которая представляет собой среднюю арифметическую из численности на начало и конец календарного периода. Показатель среднегодовой численности широко используется для расчетов среднедушевых показателей (потребления, доходов, обеспечения транспортными коммуникациями, товарами потребления, услугами и т.д.).

В основу отечественной статистики положено деление населения на городское и сельское.

К городскому населению относятся жители городских поселений, поселков городского типа, дачных поселков.

Сельское население проживает в населенных пунктах, которые классифицируются как сельские поселения.

Возрастной анализ населения, отражающий процесс воспроизводства населения, широко используется при разработке экономической и социальной политики. Выделяются:

лица моложе трудоспособного возраста;

лица трудоспособного возраста;

лица старше трудоспособного возраста.

Чем больше доля численности детей, а также лиц трудоспособного возраста, тем больше повода говорить о стабильной структуре данного общества. В противном случае речь может идти об ухудшении демографической ситуации, а следовательно, и об отсутствии позитивной перспективы для экономического развития.

Под домохозяйством понимается группа лиц, которые совместно проживают в жилищной единице и которые полностью или частично объединили свои индивидуальные бюджеты в общий бюджет, подчиняясь общим правилам как связанных, так и не связанных отношениями родства. Домохозяйства, соответствующие данным критериям, принято относить к частным домохозяйствам (домохозяйство может состоять и из одного человека, проживающего самостоятельно).

Кроме частных имеются и коллективные (групповые) домохозяйства. В этом случае речь идет о группе лиц, проживающих в одной жилищной единице, совместно питающихся, но не имеющих индивидуальных бюджетов, подчиняющихся общим правилам и обычно не связанных родственными отношениями (дома-интернаты, детские дома, дома ребенка, религиозные учреждения, воинские части и т.д.).

22. Естественное движение населения. Понятие естественного прироста населения, естественного оборота. Показатели рождаемости, плодовитости и смертности.

Изменение численности населения между переписями отслеживается с помощью текущего учета населения, который основывается на статистике естественного и миграционного (механического) движения населения.

Естественное движение населения - изменение численности населения за счет рождения и смертей. В статистике широко используется показатель естественного прироста населения, который определяют как разность между числом родившихся живыми и числом умерших за определенный период, имея в виду прежде всего положительный результат (число родившихся должно превышать численность умерших). Если разница имеет отрицательный результат, то речь идет о показателе естественной убыли населения.

Воспроизводство населения измеряется с помощью общего коэффициента рождаемости и общего коэффициента смертности (рассчитываются на 1000 человек, т.е. в промилле, ‰).

Общий коэффициент рождаемости характеризует интенсивность деторождения по отношению к населению в целом (всех возрастов) и вычисляется как отношение числа родившихся живыми в течение года (N) к среднегодовой численности населения ( ):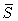

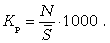(13.1)

Интенсивность смертности населения измеряется общим коэффициентом смертности, который представляет собой отношение общего числа умерших в течение года (М) к среднегодовой численности населения:

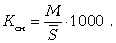(13.2)

В статистике населения используется также коэффициент естественного прироста (убыли), который представляет собой разность между коэффициентом рождаемости и коэффициентом смертности.

Большое значение для анализа естественного движения населения имеет расчет возрастных коэффициентов рождаемости (коэффициентов для отдельных возрастных групп женщин) и суммарного коэффициента рождаемости, который характеризует среднее число детей, рожденных женщиной за свою жизнь. В последние годы в России суммарный коэффициент рождаемости имеет тенденцию к снижению (суммарный коэффициент рождаемости снизился с 2,00 в 1970 г. до 1,24 в 1998 г.).

Важнейшей частью статистической информации о смертности населения является показатель смертности детей на первом году жизни. Речь идет о коэффициенте младенческой смертности, который представляет собой отношение числа умерших в возрасте до одного года (М0 ) к числу родивши