Измерение степени тесноты связи между признаками (парная корреляция).

После обнаружения корреляц. связи возникает задача установления степени тесноты

этой связи, т.е. зависимости вариации результативного признака от вариации признака факторного. К простейшим показателям степени тесноты корреляц. связи относится коэффициент корреляции знаков, предложенный Г.Фехнером, основанный на оценке степени согласованности в отклонениях отдельных значений факторного и ему соответствующего результативного признака от средних значений этих признаков:

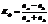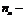, где число совпадений знаков, 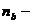число несовпадений знаков.

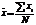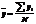; ,где N- полное число всевозможных сочетаний.

Коэффициент корреляции знаков может принимать значения от +1 до -1.Если знаки всех отклонений совпадут, то 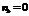, , 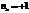если все знаки различны, то 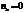, 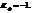Случай, когда 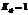, соответствует наличию между признаками прямой корреляц. связи.

Если 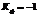, то можно предположить наличие обратной связи.

Значение 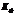не зависит от величины отклонений от средних значений, поэтому о степени тесноты связи судить не позволяет.

Более совершенным показателем степени тесноты связи является линейный коэффициент корреляции Карла Пирсона (r). При его расчёте учитывают не только знаки, но и величину отклонений от средних значений факторного и результативного признаков: 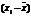, 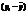. Однако непосредственно сопоставить их между собой нельзя из-за разной размерности, поэтому сравнению подлежат относительные величины отклонений, которые представляют собой нормированные отклонения:

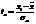-нормированное отклонение фактического,

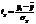- нормированное отклонение результативного.

Характеристикой степени тесноты связи между признаками для всей совокупности является среднее произведение нормированных отклонений:

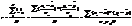
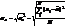- дисперсия.

Линейный коэффициент корреляции может принимать любые значения от -1 до +1.Чем ближе он по абсолютной величине к 1, тем теснее связь между признаками. Знаки «-« или «+»указывают на направление связи: «+» - связь прямая, «-« - связь обратная.

При r = 0 линейная связь между признаками отсутствует, а при 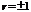связь функциональная (каждому значению факторного соответствует определённое значение результативного).

Показатель тесноты связи, найденный по данным ограниченной статистич. совокупности, может искажаться под действием случайных причин. Принципиально возможный случай, когда отклонение линейного коэффициента корреляции r от 0 целиком обусловлено случайными колебаниями выборочных данных, особенно при малом объёме выборки. Это требует проверки существенности значений r. Прежде, чем распространять результаты его распред. на генеральные совокупности.

Для оценки значимости (существенности) коэф-та r используют t- критерий Стьюдента в форме: 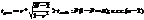. Их сравнивают с табл.

Если расч. знач. t больше, чем табл., то практически маловероятно, что найденное отклонение линейного коэф-та корреляции от 0 обусловлено случайными факторами.

Если 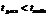, то линейная корреляция между признаками отсутствует с той же самой вероятностью.

Коэф-т линейной корреляции r довольно точно оценивает степень тесноты связи между факторным и результативным признаками, если между ними существует линейная зависимость.

Если зависимость отличается от линейной, то называется криволинейной, то r недооценивает степень тесноты связи, и в таких случаях рекомендуют использовать для характеристики тесноты связи м/д признаками хорошо известное эмпирическое корреляционное отклонение ( 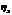) , расчет которого основан на теореме сложения дисперсий: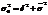

Межгрупповая дисперсия характеризует ту часть колеблемости результативного признака, которая складывается под влиянием изменения признака факторного, положенного в основу группировки.

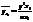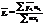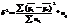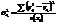; ; ; - внутригрупповая дисперси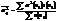я; .

Вторая составляющая 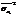оценивает ту часть вариации результативного признака, которая обусловлена действием других случайных причин: .

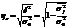Эмпирическое корреляционное отношение может изменяться в диапазоне от 0 до 1.

0 означает, что 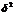близок к 0, т.е. факторный признак не оправдывает заметного влияния на рассматриваемый.

Если 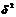близок к 1- это означает, что близка к 0 средняя внутригрупповая дисперсия, т.е. вся вариация результативного признака обусловлена действием факторного.

Промежуточные значения эмпирического корреляционного отношения от 0 до 1 дают разную степень корреляции, которую оценивают по шкале Чэддока. Эмпирическое корреляционное отношение не позволяет установить направление связи (прямая, обратная, корреляционная). Для установления направления используют данные корреляционной таблицы.

Различие м/д внутригрупповыми и межгрупповыми дисперсиями может носить случайный характер, поэтому значимость рассчит. корреляц. отношения оценивают с помощью критерия Фишера (F), табличные значения которого указывают предельное значение F- критерия для различных комбинаций числа степеней свободы сравниваемых дисперсий и уровней значимости: 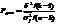, где n- общее число вариантов, k- число групп.

- Если 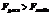, то с соответствующей вероятностью можно утверждать, что различие в величине дисперсий существенно и сделать вывод о существовании корреляции м/д факторным и результативным признаками.

- Если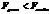

- Если 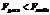,то различия м/д дисперсиями носят случайный характер с той же вероятностью.

Результат. признак слабо зависит от факторного.

Когда связь м/д признаками отклоняется от линейной формы, то эмпирическое корреляц. отношение и линейный коэффициент корреляции отлич. по величине, причем .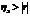

Чтобы прверить возможность использования линейной ф-ции в качестве формы уравнения связи, опред. разность квадратов м/д: .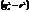

Если 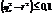, то считается возможным применение линейного уравнения для описания корреляц. зависимости м/д признаками.