Развертка поверхностей

Ранее мы отмечали, что под поверхностью понимаем границу материального тела, не имеющую третьего измерения – толщины. С позиций разверток поверхностей ее целесообразно рассматривать как гибкую нерастяжимую пленку, которая путем изгибания может быть совмещена с плоскостью. Процесс совмещения поверхности с плоскостью называется развертыванием поверхности. Поверхность, которая может быть совмещена с плоскостью без разрывов и складок, называется развертывающейся, а полученная при этом плоская фигура – разверткой. С позиций конструирования, разверткой называется такая плоская фигура, которая будучи свернута по определенному алгоритму, образует с наперед заданной точностью искомую поверхность. К развертывающимся относятся все гранные и кривые линейчатые поверхности.

Развертывание поверхностей по способу триангуляции (треугольников)

Этот способ применяется для развертывания пирамидальных и конических поверхностей.

Развертка пирамиды

Развертка полной поверхности пирамиды представляет собой совокупность основания пирамиды (плоский многоугольник) и всех ее граней (треугольников). Чтобы совместить поверхность пирамиды с плоскостью, надо найти натуральный вид всех ее граней (плоскостей). Сущность способа триангуляции заключается в приеме построения натурального вида треугольников по трем его сторонам. Для этого необходимо найти истинную величину всех его ребер.

На рис.6.1 представлена наклонная трехгранная пирамида. Для нахождения натуральной величины ребер пирамиды воспользуемся способом вращения вокруг проецирующих осей (см. рис. 2.3).

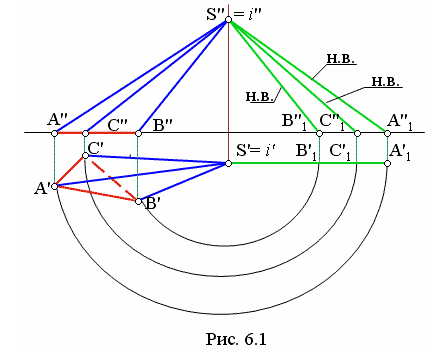
На рис. 6.1 горизонтальные проекции ребер поворачиваются вокруг i' в положение параллельное оси Х (S'В'₁; S'С'₁; S'А'₁). На фронтальной плоскости их проекции S"В"₁; S"С"₁; S"А"₁ отобразились в натуральную величину. Основание АВС расположено параллельно горизонтальной плоскости, следовательно, А'В'С'также отобразилось в натуральную величину.

На рис. 6.2 показана развертка полной поверхности пирамиды. Боковые грани (треугольники S₀A₀B₀, S₀B₀C₀, S₀A₀C₀) построены по трем сторонам.

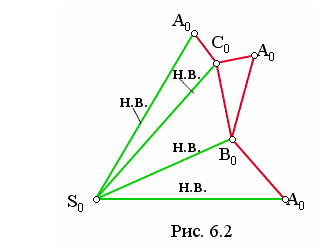
Развертка конической поверхности

Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор радиуса L c углом при вершине равным 360° *R/L [8, стр. 207]

Для построения приближенной развертки наклонного (эллиптического) конуса в поверхность вписывают не менее чем двенадцатигранную пирамиду и строят развертку по приведенному выше способу триангуляции. При этом ломаную линию основания A₀B₀C₀A₀, а также основание A₀B₀C₀ сглаживают лекальной кривой.

Развертывание поверхностей по способу нормального сечения

Способ нормального сечения применяется для развертывания призматических и цилиндрических поверхностей.

Развертка призмы

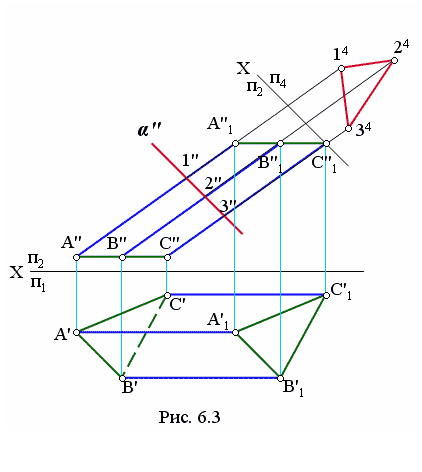
Нормальным сечением призмы называется ее сечение плоскостью α", проведенной перпендикулярно к ребрам граней. На рис. 6.3 это сечение 1" 2" 3". Чтобы найти натуральную величину этого сечения надо выполнить замену плоскостей проекций: вводим новую π₄ перпендикулярно к π₂ и располагаем ее параллельно α". На горизонтальной плоскости измеряем расстояния от ребер АВС до оси Х и откладываем в плоскости п₄.

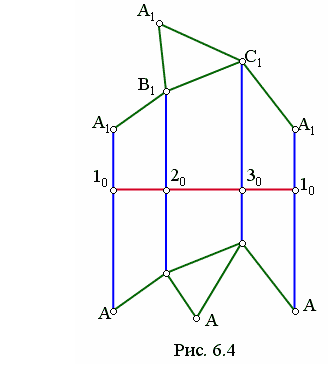
На рис. 6.4 выполнено построение развертки призмы, где ломаная линия нормального сечения 1⁴ 2⁴ 3⁴1⁴ развернута в прямую. Из точек 1₀ 2₀ 3₀ 1₀ проведены перпендикуляры, на которых соответственно отложена натуральная величина расстояний от точек А" до 1" (на рис. 6.4 это А 1₀ ) и от 1" до А "₁ (на рис. 6.4 это 1₀А₁). Аналогичные построения выполнены для остальных ребер. Основание построено по способу триангуляции.

На рис. 6.3 призма задана таким образом, что ее боковые ребра являются прямыми уровня и на фронтальной плоскости они отобразились в натуральную величину. Если же ребра будут прямыми общего положения, чертеж надо преобразовать способом замены так, чтобы они стали прямыми уровня и после этого выполнить построение развертки.