Прямоугольное (ортогональное) проецирование
Метод проекций
Образование проекций
В основу метода Начертательной геометрии положен Метод проецирования. Слово «проецирование» - латинского происхождения, что означает «бросать вдаль». Таким образом, под проекцией предмета на плоскость подразумевают его изображение, «отброшенное» на эту плоскость с помощью лучей, подобно тому, как предмет, освещенный солнцем, отбрасывает свою тень на землю.
Центральное и параллельное проецирование
Из сказанного следует, что для построения проекций необходим аппарат проецирования, который включает в себя (рис.1.1):
o источник лучей, пусть это будет точка S (в дальнейшем лучи будем называть проецирующими);
o плоскость, на которой будем получать изображение – π0 (в дальнейшем - плоскость проекций);
o проецируемый объект, пусть это будет точка А . Для построения проекции проводим проецирующий луч из центра S через точку А до пересечения с плоскостью π0 .
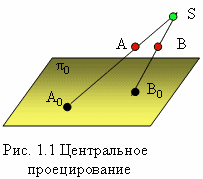
Точка А0 – является проекцией точки А на плоскость π0 из центра S . Данный вид проецирования называется центральным .
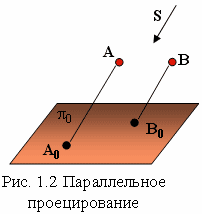
Если центр проекций удален в бесконечность, то проецирующие лучи будут параллельны друг другу. В этом случае направление проецирования задается стрелкой (рис. 1.2.), а проецирование называется параллельным .
Геометрические фигуры в общем случае проецируются на плоскость проекций с искажением. Проекции не сохраняют линейные и угловые величины оригинала. Характер этих искажений зависит от положения геометрической фигуры в пространстве, от аппарата проецирования и от положения плоскости проекций.
Однако некоторые геометрические свойства фигур остаются неизменными в процессе проецирования. Такие свойства называются независимыми или инвариантными для данного аппарата проецирования.
Основные свойства параллельного проецирования приведены в работе [2 , стр. 8]., см. также в работе Андрющенко К.Е. «Метод проекций».
Прямоугольное (ортогональное) проецирование
Прямоугольное проецирование является частным случаем параллельного проецирования, когда направление проецирующих лучей Sперпендикулярно к плоскости проекций π0, рис. 1.3.
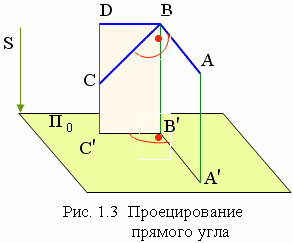
Для прямоугольного проецирования справедливы все свойства параллельных проекций. Кроме того, для прямоугольного проецирования необходимо отметить еще одно очень важное свойство: если одна сторона прямого угла (AB)параллельна плоскости проекций (π0), а другая (BC) не перпендикулярна, то на эту плоскость проекций (рис.1.3) прямой угол проецируется без искажения, то есть в свою натуральную величину (Н.В.): угол АВС равен углуА'В'С'. О проецировании плоских углов см. [2, стр. 31]
При рассматриваемом аппарате проецирования каждой точке пространства соответствует только одна точка на плоскости. Однако при проецировании на одну плоскость не выполняется требование Начертательной геометрии о том, что чертеж должен быть обратимым, поскольку одной точке на плоскости может соответствовать бесконечное множество точек, расположенных на восстановленном проецирующем луче.
