Поверхности вращения. Главные линии поверхности. Принадлежность точки к поверхности

Поверхностью вращения называют поверхность, которая образуется произвольной кривой при ее вращении вокруг неподвижной оси. Ниже приведены примеры поверхностей вращения.

На рис. 3.3 – 3.4 представлены разновидности тора. Тором называется поверхность, которая получается при вращении окружности вокруг оси. Открытый тор (или кольцо), когда окружность не пересекается с осью. Если окружность пересекается с осью или касается ее, поверхность называется закрытым тором. Глобоид – поверхность, образованная вращением дуги окружности вокруг оси, расположенной с внешней стороны дуги. Параболоид образуется при вращении параболы вокруг ее оси. Однополостный гиперболоид образуется при вращении гиперболы вокруг мнимой оси или при вращении прямой линии (отрезка) вокруг оси, скрещивающейся с этой прямой.

Сфера образуется при вращении окружности вокруг оси, проходящей через ее центр.

На рис. 3.9 представлен чертеж сферы. При проецировании сферы на горизонтальную плоскость часть проецирующих лучей (выделены синим цветом), осветят верхнюю половину сферы, а часть лучей коснется поверхности.

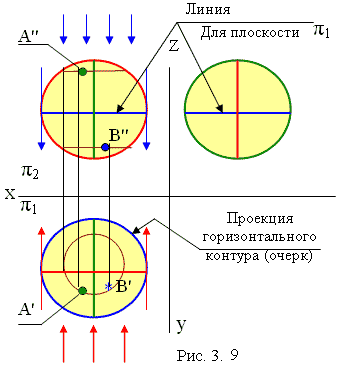
Линия касания проецирующих лучей с поверхностью называется контурной линией. Проекция контурной линии на одну плоскость (в данном случае на горизонтальную) дает очертание (очерк)поверхности, а на другую (на фронтальную) – линию видимости. Аналогично при проецировании на фронтальную плоскость - контурная линия красного цвета; на профильную – зеленого.

Для построения точки, принадлежащей поверхности, через точку проводят линию (на поверхности сферы это окружность) и по линиям связи строят вторую проекцию точки.

На чертеже условимся обозначать видимые точки в виде окружности . Невидимые - в виде звездочки *.

Пусть задана фронтальная проекция точки А (А") - рис. 3.9. По условию точка принадлежит поверхности и на фронтальной она видимая. Для построения ее горизонтальной проекции через точку проводим параллель, то есть линию, параллельную горизонтальному контуру. По линиям связи строим горизонтальную проекцию параллели (окружность). Точка А принадлежит данной параллели. Принимая во внимание, что точка А расположена выше линии видимости для плоскости π₁, изображаем ее горизонтальную проекцию как видимую. Кроме того, чтобы она была видимой и на фронтальной плоскости (она так задана по нашему условию), располагаем ниже красной линии видимости для плоскости π₂.

Точка В (В") на фронтальной плоскости расположена ниже линии видимости для π₁, следовательно, ее горизонтальная проекция изображена звездочкой, то есть невидимой точкой. Но на горизонтальной - она так же, как и точка А, расположена ниже красной линии, так как по условию данной задачи на фронтальной она задана как видимая.