Процессы изменения состояния газов
Л.М. Дыскин, Н.Т. Пузиков
РАСЧЕТ ТЕРМОДИНАМИЧЕСКИХ ЦИКЛОВ
Учебное пособие
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
НИЖЕГОРОДСКИЙ ГСУДАРСТВЕННЫЙ АРХИТЕКТУРНО – СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Л.М. Дыскин, Н.Т. Пузиков
РАСЧЕТ ТЕРМОДИНАМИЧЕСКИХ ЦИКЛОВ
Учебное пособие
Нижний Новгород, 2000
ББК 38. 113
Д 87
П 88
Дыскин Л.М., Пузиков Н.Т. Расчет термодинамических циклов:
Учебное пособие. – Н.Новгород: Нижегород. гос. архит. – строит. ун – т, 2000. – 87 с. ISBN – 5 – 87941 – 123 – 0.
Приведены теоретические сведения о термодинамических процессах, рассмотрены методики расчета газовых, паровых и холодильных циклов, даны примеры расчета термодинамических циклов и варианты контрольных заданий.
Предназначено для студентов специальности 290700 “Теплогазоснабжение и вентиляция” и является дополнением к курсу “Техническая термодинамика”.
Тем. план 2000 ББК 38. 113
ISBN 5 – 87941 – 123 – 0 ã Дыскин Л.М.,
Пузиков Н.Т., 2000.
ВВЕДЕНИЕ
Важная роль в разработке новых устройств и технологических процессов принадлежит теплотехнике, в теоретическую базу которой входит техническая термодинамика. Наиболее существенную роль в термодинамике играют тепловые процессы, поэтому изучению таких процессов придается большое значение. Глубокое знание термодинамических процессов позволяет создавать и эксплуатировать теплотехническое оборудование строительной индустрии на более высоком качественном уровне.
Учебное пособие состоит из трех частей: расчет газового цикла, расчет парового цикла и расчет холодильного цикла. Рассмотрены теоретические основы, приведены аналитические зависимости и примеры расчетов циклов. Даны варианты домашних заданий.
Задание 1. РАСЧЕТ ГАЗОВОГО ЦИКЛА
Цикл отнесен к 1 кг воздуха. Принимаем Ср = 1,0 кДж/кг·К, Сv = 0,71 кДж/кг·К и R = 290 Дж/кг·К.
Требуется:
1. Определить параметры p, v, T, u, h всех основных точек цикла.
2. Для каждого процесса, входящего в состав цикла, определить n, c, Δu, Δh, Δs, l, q, а также a и b (доли теплоты процесса, идущие на изменение внутренней энергии и на работу).
3. Построить цикл в масштабе в p – v, T – s, lg p – lg v – координатах. При построении наносят основные точки цикла; кривые процессов строятся по трем промежуточным точкам, а одну из политроп в p – v - координатах строят по логарифмическим координатам.
4. Определить работу цикла lц, термический к.п.д. ht и среднее индикаторное давление pi.
5. Полученные данные поместить в таблицы, формы которых приведены в примере расчета газового цикла.
Примечание. Данные к заданию № 1 составлены в форме циклов, приведенных ниже. Вариант задания выбирается по указанию преподавателя.
Процессы изменения состояния газов
Все реальные процессы изменения состояния газа, происходящие в различных тепловых установках, являются неравновесными. Однако в технической термодинамике для упрощения расчетов их заменяют соответствующими равновесными процессами.
К основным процессам, имеющим важное значение как для теоретических исследований, так и для практических работ, относятся изохорный, изобарный, изотермический и адиабатный. Кроме того, существует обобщающий процесс (политропный), по отношению к которому перечисленные процессы являются частными случаями.
Для всех процессов устанавливается общий метод исследований, состоящий в следующем:
1. Записывают уравнение кривой процесса в p-v и T-s – координатах.
2. Устанавливают зависимость между основными параметрами рабочего
тела в начале и конце процесса.
3. Определяют изменение внутренней энергии по формуле, справедливой
для всех процессов идеального газа
t2 t2 t1
Δu = u1 - u2 =∫Cvdt = Cvm│t2 - Cvm│t1 (1.1)
t1 0 0
или при постоянной теплоемкости
u2 - u1 = Cv(t2 - t1). (1.2)
4. Определяют работу изменения объема газа
v2
l = ∫pdv. (1.3)
v1
5. Определяют количество теплоты, участвующей в процессе
t2 t2 t1
q1-2 =∫Cxdt=Cxm│t2 - Cxm│t1 (1.4)
t1 0 0
6. Определяют изменение энтальпии по формуле, справедливой для всех процессов идеального газа
t2 t1
h1-h2 = Cpm│t2-Cpm│t1 (1.5)
0 0
или при постоянной теплоемкости
h2-h1=Cp(t2-t1) (1.6)
7. Определяют изменение энтропии идеального газа
S2-S1 = Cv ln 
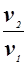= Cp 
- 
(1.7)
Изохорный процесс
Процесс, протекающий при постоянном объеме, называют изохорным.
Уравнение кривой процесса в диаграмме p-v имеет вид v = const, а линия, изображающая этот процесс графически, называется изохорой (рис.1.1). Примером изохорного процесса может служить охлаждение или нагревание газа в закрытом сосуде. Связь между термическими параметрами начального и конечного состояния газа выражается законом Шарля
(1.8)
Внешняя работа газа при постоянном объеме
v2
l = ∫ pdv = 0, (1.9)
v1
так как dv = 0. Это значит, что в изохорном процессе вся подведенная ( или отведенная) теплота идет на увеличение ( или уменьшение) внутренней энергии, т.е.
qv = ΔUv
 |
6
Следовательно, количество теплоты, участвующей в процессе при постоянной теплоемкости, равно
qv1-2 = Cv(T2-T1)= u2-u1 (1.10)
В некоторых случаях следует учитывать зависимость теплоемкости от температуры. Тогда теплота изохорного процесса определится следующим образом:
t2 t1
qv1-2 = u2-u1= Cvm│t2 - Cvm│t1 (1.11)
0 0
Изменение энтропии в изохорном процессе определится из следующего уравнения:
S2 -S1 = Cv ln 
= Cv ln 
(1.12)
Изохора на T-s – диаграмме представляет собой логарифмическую кривую (рис.1.1.).
Изобарный процесс.
Процесс, протекающий при постоянном давлении, называется изобарным. Линия, изображающая этот процесс графически, называется изобарой и в координатах p-v выражается уравнением p = const (рис 1.1.). В соответствии с
законом Гей-Люссака связь между термическими параметрами начального и конечного состояний выразится следующим образом:
= 
. (1.13)
Удельная работа изменения объема в изобарном процессе
v2
l = p ∫dv = p(v2-v1), (1.14)
v1
или
l = R·(T2-T1). (1.15)
Количество теплоты, сообщенной телу в изохорном процессе при постоянной теплоемкости,
qp1-2 = Cp(t2-t1)=h2-h1, (1.16)
при переменной теплоемкости
t2 t1
qp1-2 =Cpm│t2-Сpm│t1 = h2-h1. (1.17)
0 0
Изменение энтропии при p = const
S2-S1 =Cp ln 
Cp ln 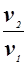. (1.18)
Изобара на T-s – диаграмме изображается логарифмической кривой (рис. 1.1.), более пологой, чем изохора.