Последовательность решения задачи. ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ

ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ

1. В соответствии с заданием начертить чертеж фигуры сложной формы в масштабе и проставить ее размеры.

2. Разбить чертёж фигуры на простейшие составные части, показать центр тяжести каждой из них.

3. Провести оси координат так, чтобы они охватывали всю фигуру (если фигура не симметричная, желательно располагать плоскую фигуру в первой четверти системы координатных осей).

4.Используя знания по определению центра тяжести простейших плоских фигур (рис. 1), заполнить таблицу 1

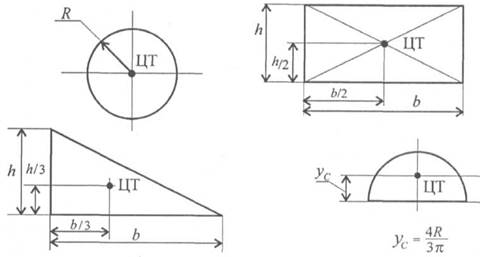
Рис. 1 - Центры тяжести простейших плоских фигур

Таблица 1

№ п/п	Простейшая фигура	Площадь сечения, Аi, см2	Расстояние до центра тяжести простой фигуры
по оси абсцисс, хi, см	по оси ординат, yi, см

5. Вычислить координаты центра тяжести всей фигуры аналитическим способом.

Координаты центра тяжести всей фигуры Х _с и У_с определяют по формулам:

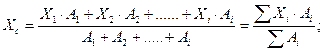
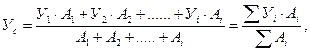
где Х ₁, Х ₂….Х _i - расстояние от оси У до центра тяжести простой фигуры, см;

У ₁, У ₂….У _i - расстояние от оси Х до центра тяжести простой фигуры, см;

А ₁, А ₂….А _i - площадь простой фигуры, см ².

Если сложная фигура имеет отверстие в виде геометрических фигур, то эти площади необходимо ввести в формулу со знаком «минус». Этот метод называется методом отрицательных площадей.

6. Проверить правильность решения задачи, используя другой метод разбивки.

Пример 1.Определить координаты центра тяжести плоской фигуры, изображённой на рисунке 2, если известно a = 40 см, b =100 см, r = 20 см .

Рис. 2 - Схема задачи

Решение:

1. Разбиваем чертёж фигуры на простейшие составные части: прямоугольник, треугольник, полукруг, обозначаем центр тяжести каждой из них и располагаем чертёж фигуры в первой четверти координатных осей (рис. 3).

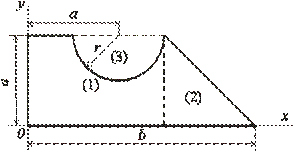
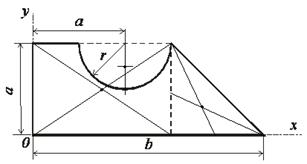
Рис. 3 - Разбиение на части

2. Заполняем таблицу

№ п/п	Простейшая фигура	Площадь сечения, Аi, см2	Расстояние до центра тяжести простой фигуры
по оси абсцисс, хi, см	по оси ординат, yi, см
	прямоугольник
	треугольник		73,3	13,3
	- полукруг			31,5

а) Площади сечения простейших фигур

для прямоугольника А₁ = 40 × 60 = 2400 см²

для треугольника А₂ = 40 × 40 / 2 = 800 см²

для полукруга А₁ = p × 20² / 2 = 628 см²

б) Центры тяжестей рассматриваемых частей фигуры имеют следующие координаты:

для прямоугольника х₁ = 30 см, y₁ = 20 см;

для треугольника х₂ = 60+40/3=73,3 см, y₂ = 40/3=13,3 см;

для полукруга х₃ = 40 см, y₃ = 40-4·20/(3·π) =31,5 см.

3. Вычисляем координаты центра тяжести фигуры по формулам

Х_с = (2400×30 + 800×73,3 - 628×40) / (2400 + 800 - 628) = 41 см

Y_c = (2400×20 + 800×13,3 - 628×31,5) / (2400 + 800 - 628) = 15,1 см

Ответ: С (41;15,1)

Проверка:

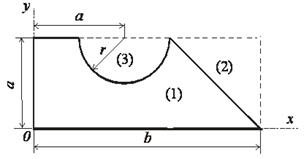
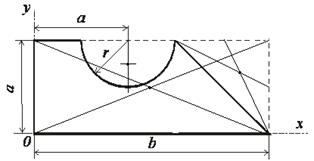
№ п/п	Простейшая фигура	Площадь сечения, Аi, см2	Расстояние до центра тяжести простой фигуры
по оси абсцисс, хi, см	по оси ординат, yi, см
	прямоугольник
	- треугольник		86,7	26,7
	- полукруг			31,5

Х_с = (4000×50 - 800×86,7 - 628×40) / (4000 - 800 - 628) = 41 см

Y_c = (4000×20 - 800×26,7 - 628×31,5) / (4000 - 800 - 628) = 15,1 см

Ответ: С (41;15,1)

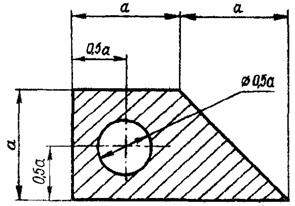
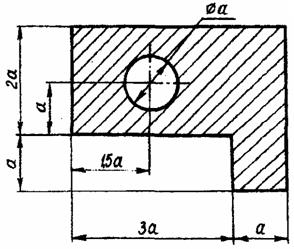
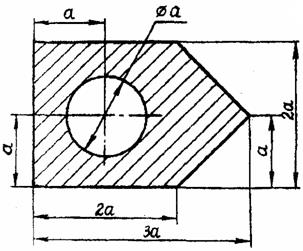
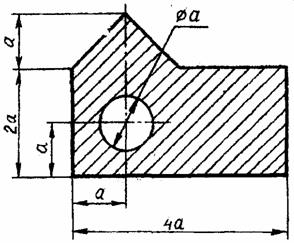
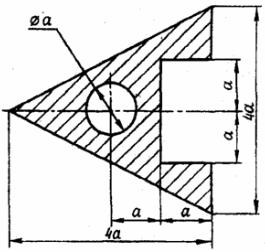
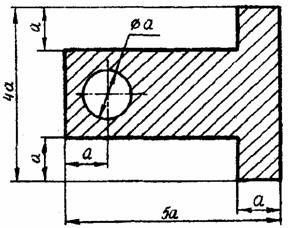
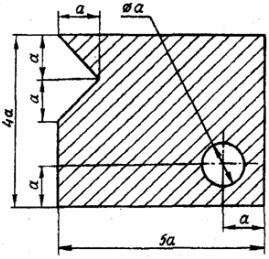
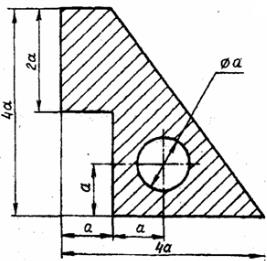
Задача 1. Определить координаты центра тяжести плоской фигуры (рисунок 4). Данные своего варианта взять из таблицы 2

Таблица 2 - Исходные данные

Номер схемы на рисунке 4	a
Варианты	см

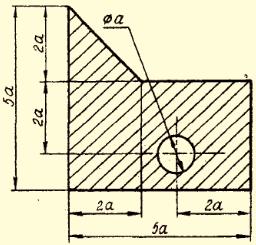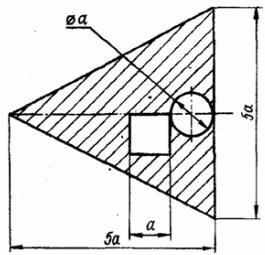Рис. 4 - Схема задачи

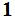
Задача 2. Определить координаты центра тяжести плоской фигуры (рисунок 5). Данные своего варианта взять из таблицы 3

Таблица 3 - Исходные данные

Номер схемы на рисунке 5

a

b

r

Варианты

см

см

см

1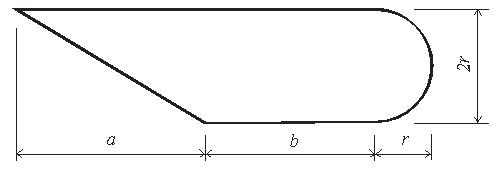
2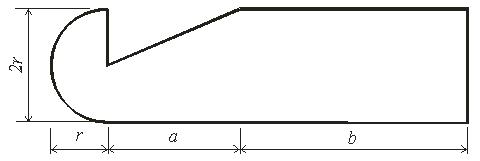
3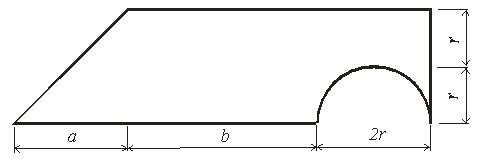
4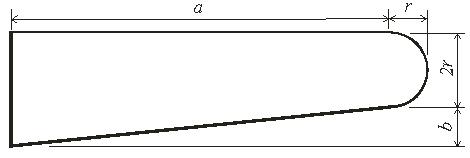
5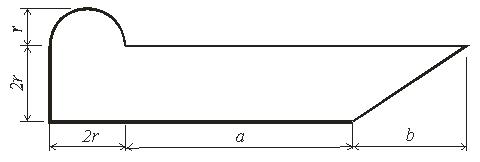
6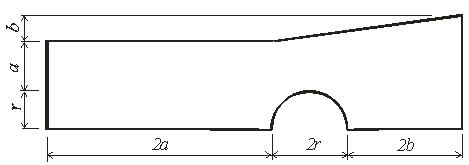
7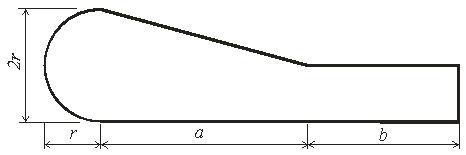
8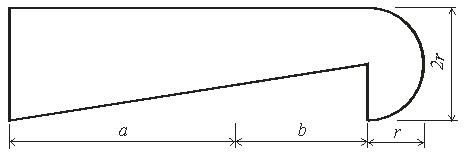
9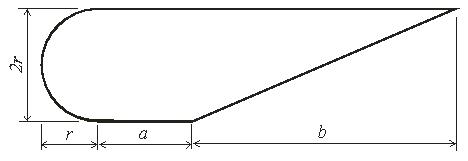
10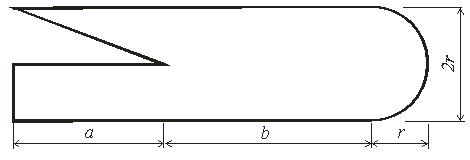

Рис. 5 - Схема задачи