Аксонометрические проекции

Во многих случаях при выполнении технических чертежей наряду с изображением предметов в ортогональных проекциях требуется иметь их более наглядные изображения. Для построения таких изображений применяют проекции, называемые аксонометрическими. Способ аксонометрического проецирования состоит в том, что данная фигура вместе с осями прямоугольных координат, к которым она отнесена, параллельно проецируется на некоторую плоскость, которую иногда называют картинной.

Если направление проецирующих лучей перпендикулярно к картинной плоскости, аксонометрию называют прямоугольной, в противном случае косоугольной. При проецировании на картинную плоскость значения прямоугольных координат всех точек предмета искажаются. Величина этих искажений называется показателями или коэффициентами искажений. Если коэффициенты искажений по всем трем осям (Х,Y,Z) не равны между собой – аксонометрия называется триметрией. Если коэффициенты искажений по каким либо двум осям равны - аксонометрия называется диметрией. Если коэффициенты по всем трем осям равны - аксонометрия называется изометрией.

Государственный стандарт устанавливает пять видов аксонометрических проекций: два вида прямоугольных и три косоугольных аксонометрических проекций.

Более подробно порядок построения точек и предметов в аксонометрических проекциях можно посмотреть в работах [1, стр.234] и [8, стр. 219].

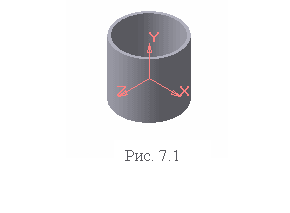
На рис. 7.1 изображена прямоугольная изометрия прямого кругового цилиндра.

Вопросы для подготовки к экзаменам по Начертательной геометрии и Инженерной графике
(Знать с обязательным приведением примеров - чертежей)

1. Метод проекций. Центральное и параллельное проецирование. Основные свойства параллельного проецирования. Обратимость чертежей. Пространственная и плоская модель координатных плоскостей пространства. Точка в системе трех плоскостей проекций. Проекции точек, расположенных в различных углах (октантах) пространства.

2. Прямоугольные проекции геометрических фигур. Чертеж отрезков прямых. Прямые общего (О.П.) и частного (Ч.П.) положения. Взаимное положение прямых. Определение видимости точек на чертеже (конкурирующие точки). Следы прямой.

3. Плоскость. Способы задания плоскости на чертеже. Следы плоскости. Плоскости О.П. и Ч.П. Принадлежность прямой и точки к плоскости. Главные линии плоскости (горизонталь, фронталь, линия наибольшего ската).

4. Поверхность. Главные линии поверхности. Контурная линия. Проекции контурных линий на чертеже (очертание, линия видимости). Принадлежность точки к поверхности.

5. Поверхности вращения. Принадлежность точки к поверхности. Разнообразие форм поверхностей вращения.

6. Линейчатые поверхности. Наклонный (эллиптический) конус. Наклонный (эллиптический) цилиндр. Принадлежность точки к поверхности.

7. Призматические и пирамидальные поверхности. Определение видимости ребер поверхностей. Принадлежность точки к поверхности.

8. Способы преобразования прямоугольных проекций. Способ перемены плоскостей: Задача 1. Прямую О. П. преобразовать в прямую уровня. Задача 2. Прямую О. П. преобразовать в проецирующую прямую. Задача 3. Плоскость О. П. преобразовать в проецирующую. Задача 4. Плоскость О. П. преобразовать в плоскость уровня.

9. Способы преобразования прямоугольных проекций. Способ вращения. Вращение вокруг осей, расположенных перпендикулярно к плоскостям проекций: прямую О. П. преобразовать в прямую уровня.

10. Способы преобразования прямоугольных проекций. Способ вращения вокруг осей, расположенных параллельно к плоскостям проекций: плоскость О. П. преобразовать в плоскость уровня.

11. Позиционные задачи. Общий алгоритм нахождения точек, одновременно принадлежащих двум множествам. Пересечение прямой О. П. с плоскостью О. П.

12. Позиционные задачи. Взаимное пересечение плоскостей.

13. Позиционные задачи. Пересечение поверхностей проецирующей плоскостью и построение натурального вида (Н. В.) плоского сечения.

14. Позиционные задачи. Пересечение прямой О. П. с поверхностями.

15. Позиционные задачи. Пересечение поверхностей. Способ секущих плоскостей.

16. Позиционные задачи. Пересечение поверхностей. Способ концентрических сфер.

17. Позиционные задачи. Пересечение поверхностей. Способ эксцентрических сфер.

18. Метрические задачи. Проецирование прямого угла. Условие перпендикулярности прямой и плоскости.

19. Метрические задачи. Определение расстояний между: двумя точками; точкой и прямой; двумя параллельными прямыми; точкой и плоскостью; плоскостью и параллельной ей прямой.

20. Метрические задачи. Условие перпендикулярности двух плоскостей.

21. Метрические задачи. Определение углов наклона прямых уровня и прямых О. П. к плоскостям проекций.

22. Метрические задачи. Определение углов между прямыми О. П. и плоскостями О. П.

23. Метрические задачи. Определение углов между двумя плоскостями О. П.

24. Метрические задачи. Определение расстояний от точки до плоскости О. П.

25. Метрические задачи. Определение расстояний от точки до прямой О. П.

26. Аксонометрические проекции.

27. Развертывание поверхностей. Способ триангуляции (треугольников).

28. Развертывание поверхностей. Способ нормального сечения.

Уметь (по заданным исходным чертежам):

o Определять местоположение точек, расположенных в различных углах пространства.

o Строить следы плоскости, заданной: тремя точками; точкой и прямой; двумя параллельными прямыми, пересекающимися прямыми.

o Достраивать недостающую проекцию (фронтальную или горизонтальную) точки (А), лежащей в плоскости, заданной: тремя точками; двумя параллельными прямыми; точкой и прямой; следами.

o Достраивать недостающую проекцию (фронтальную или горизонтальную) плоских фигур (треугольника или многоугольника), принадлежащих плоскости.

o Определять точки пересечения прямой О. П. с поверхностями: конуса (прямого и наклонного); цилиндра; сферы; с гранными (пирамида, призма).

o Строить линию взаимного пересечения двух плоскостей, в том числе, заданных следами.

o Определять Н. В. плоской фигуры способами перемены плоскостей проекций, вращением вокруг оси, расположенной параллельно плоскостям проекций.

o Строить горизонтальные, фронтальные сечения поверхностей конуса, цилиндра, сферы, пирамиды, призмы проецирующими плоскостями.

o Строить линии пересечения поверхностей конуса, цилиндра, сферы, пирамиды, призмы плоскостями О. П.

o Строить линии взаимного пересечения поверхностей (второго порядка, линейчатых, призматических, пирамидальных).

o Строить развертки поверхностей.

Тема 10

Инженерная графика. Раздел "Инженерная графика"