Изотермический процесс

Процесс, протекающий при постоянной температуре, называется изотермическим. Линия, изображающая изотермический процесс графически,

называется изотермой и в p-v – диаграмме представляет собой гиперболу, которая соединяет точки начального и конечного состояния газа (рис. 1.1.).

Для изотермического процесса идеального газа

p₁v₁ = p₂v₂ , (1.19)

или

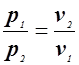. (1.20)

При T = const количество подведенной к рабочему телу теплоты численно равно работе изменения объема, т.е.

q_t1-2 = l = p₁v₁ ln 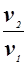= p₁v₁ ln 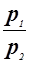. (1.21)

Энтальпия и внутренняя энергия идеального газа в изотермическом процессе не меняются и равны нулю

dh=0; du=0.

Изотермический процесс на T-s – диаграмме изображается прямой, параллельной оси абсцисс (рис.1.1.).

Изменение энтропии определится из следующего уравнения:

S₂-S₁=R ln 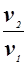= R ln 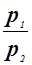. (1.22)

Теплоту, участвующую в изотермическом процессе, можно определить по формуле:

q = T(S₂-S₁). (1.23)

Адиабатный процесс

Адиабатным называется процесс, в котором к системе не подводится и от системы не отводится теплота, т.е. процесс протекает без теплообмена с окружающей средой, поэтому

dq = 0. (1.24)

Обратимый адиабатный процесс можно осуществить в цилиндре с абсолютно нетеплопроводными стенками при бесконечно медленном перемещении поршня. В общем случае для обратимого процесса

dq = T·ds, (1.25)

поэтому для обратимого адиабатного процесса

ds = 0 и s = const, (1.26)

т.е. энтропия системы сохраняется постоянной. Обратимый адиабатный процесс является одновременно изоэнтропным процессом.

Уравнение адиабаты идеального газа записывается в следующем виде:

Pv^k = const, (1.27)

где k – показатель адиабаты.

На диаграмме p-v адиабата протекает круче изотермы и является неравнобокой гиперболой (рис.1.1.), а на диаграмме T-s изображается вертикальной прямой.

Из уравнения адиабаты следует, что

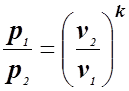
и 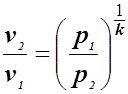. (1.28)

Эти выражения дают возможность получить соотношения между температурами и объемами

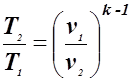, (1.29)

или между температурами и давлениями

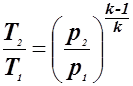. (1.30)

Работа при адиабатном процессе совершается только за счет уменьшения внутренней энергии

l = u₁-u₂ (1.31)

и её можно определить из следующих выражений:

l = 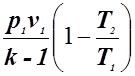; (1.32)

l = 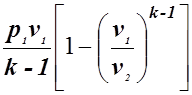; (1.33)

l = 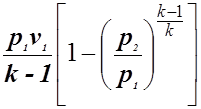. (1.34)

Все записанные выше зависимости между p, T, v справедливы при условии k = const. В реальных процессах показатель адиабаты k = 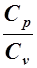зависит от температуры. Тогда в расчетах принимают среднее значение k, которое соответствует изменению температуры в процессе

k = C_P

Политропные процессы

Политропным процессом является такой термодинамический процесс изменения параметров состояния рабочего тела, при котором в течение всего процесса теплоемкость с и показатель политропы n, который может иметь любое значение в пределах от - ∞ до + ∞, остаются постоянными.

Уравнение политропного процесса имеет вид

pv 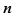= const, (1.36)

где n – показатель политропы.

Политропный процесс является обобщающим по отношению к рассмотренным термодинамическим процессам – изохорному, изобарному, изотермическому, адиабатному. Каждому частному процессу соответствует следующее значение величины показателя политропы n:

изохорному – n = ± ∞;

изобарному – n = 0;

изотермическому – n = 1;

адиабатному – n = k = const.

Физический смысл показателя политропы определяется следующим уравнением :

12

n = 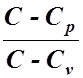. (1.37)

Значения показателя политропы n определяет расположение и характер протекания политропного процесса (рис.1.1.).

Связь между параметрами газа в двух состояниях при политропном процессе выражается формулами

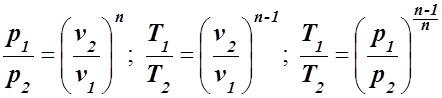(1.38)