Пример выполнения работы. Практикум (лабораторный)

Практикум (лабораторный)

Практикум состоит из 9 лабораторных работ.

Для успешного выполнения лабораторных работ необходимо изучение соответствующих модулей теоретического блока (лекций).

Общие требования к содержанию, оформлению и порядку выполнения

Перед выполнением лабораторной работы необходимо создать папку «Ваша фамилия_Lab №_variant№_» (Использовать только буквы латинского алфавита. Например: «Ivanov I.P. Lab №1_variant№5»). В эту папку в ходе выполнения работы необходимо сохранять требуемые материалы.

Лабораторные работы необходимо выполнять согласно своему варианту. Вариант назначается преподавателем.

Перед выполнением лабораторной работы изучите теоретическую часть, далее необходимо изучить пример выполнения лабораторной работы, а затем приступать к выполнению своего варианта лабораторной работы.

Задания лабораторной работы необходимо выполнять последовательно, при необходимости результат выполнения сохранять в свою папку. Папку с результатами необходимо заархивировать, создав один файл архива в формате ZIP. Файлу архива необходимо дать имя в формате: «Ваша фамилия_Lab №_variant№_.zip» (Использовать только буквы латинского алфавита. Например: «Ivanov I.P. Lab №1_variant№5.zip»). Полученный файл архива необходимо загрузить на страницу задания «Лабораторная работа №__».

Способ оценки результатов выполненных работ:

Лабораторная работа №1-4. Построение комплексных чертежей

Цель работы:

Изучить методы построения комплексных чертежей

Теоретическая часть

Материал темы 1

Общая постановка задачи

1. Построить три проекции пирамиды по координатам ее вершин, заданным в таблице 1.

2. Определить положение ребер и граней пирамиды относитель­но плоскостей проекций П₁, П₂, П₃.

3.Построить развертку поверхности пирамиды

3. Определить натуральную величину всех ребер пирамиды.

4. Через точку К, заданную координатами в таблице, провести фронтально-проецирующую плоскость Σ под углом 30 к плоскости П 1.

5. Достроить проекции и натуральный вид сечения пирамиды плоскостью Σ.

Натуральную величину ребер общего положения и натуральный вид сечения пирамида определить способом замены плоскостей проекций.

Список индивидуальных данных

Таблица 1 - Координаты точек, мм

Ва-ри-ант

А

В

С

S

К

x

y

z

x

y

z

x

y

z

x

y

z

x

y

z

Пример выполнения работы

Образец выполненной работы приведен на рис.1.

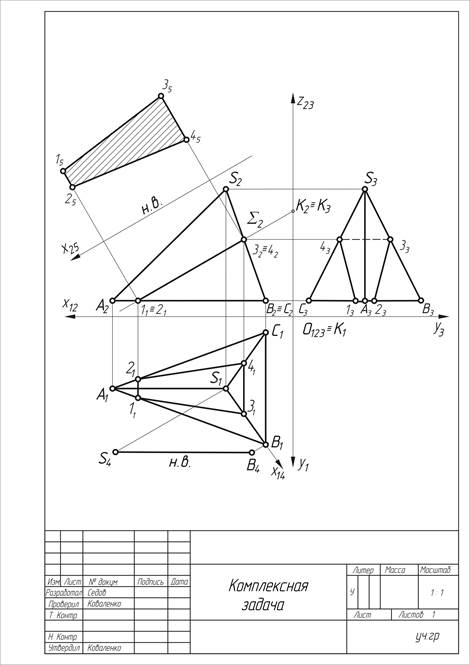
Рис.1. Образец графической работы

Комплексная задача выполняется на листе формата А4 в масштабе 1:1 в следующем порядке:

1) оформить лист формата А4 рамками с основной надписью по форме 1 (рис.3), приведенной в хрестоматии;

2) разместить проекции осей:

Х_1,2 - посредине свободного поля;

Z_2,3 - на расстоянии максимального значения координаты «Y» плюс 5 мм от правой линии рамки;

3) построить три проекции точки А (рис.2).Для этого отложить

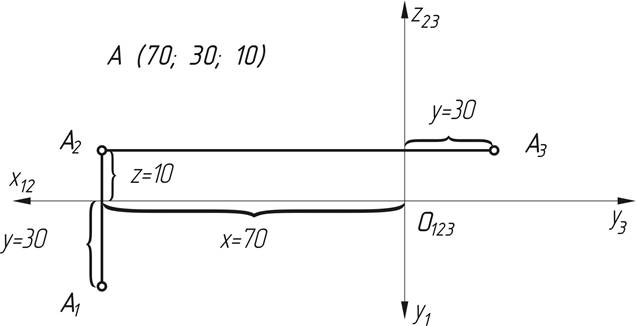
Рис.2. Построение комплексного чертежа вершины А

координату "Х" на оси Х₁₂, через полученную точку провести вертикальную линию связи; на линии связи вверх от оси Х₁₂ отло­жить координату "Z" и обозначить проекцию А₂; вниз на линии свя­зи отложить координату "У" и обозначить А₁; через А₂ провести го­ризонтальную линию связи; на ней от оси Z₂₃ отложить координа­ту "У" и обозначить А₃;

4) аналогично построить три проекции точек В, С, S ;

5) одноименные проекции вершин соединить прямыми линиями (рис.3);

6) определить положение и натуральную величину (н.в.) ребер пирамиды частного положения (рис.4,5);

7) определить натуральную величину ребра общего положения (рис.6);

8) построить три проекции точки К и провести фронтальную проекцию плоскости Σ (рис.7);

9) определить проекции сечения пирамиды плоскостью Σ, как фигуру, полученную путем соединения прямыми линиями точек пересе­чения плоскости Σ с рёбрами пирамиды;

10) построить натуральную величину сечения пирамиды плос­костью Σ (рис.8);

11) обвести построение, изобразив точки окружностями диа­метром до 2 мм, линии связи и оси - тонкими сплошными линиями, видимые ребра пирамиды и проекции сечения - толстыми сплошными, невидимые ребра пирамиды и проекции сечения - штриховыми;

12) выполнить обозначения согласно образцу (рис.1) и рис.9 шрифтом 5 мм.

13) заполнить основную надпись: графы 1,2,9 - шрифтом 7 мм с обязательным выполнением вспомогательной сетки (рис.10), все остальные графы - шрифтом 3,5 мм.

14) на обратной стороне листа выполнить развертку поверхности пирамиды, используя натуральные величины ребер.

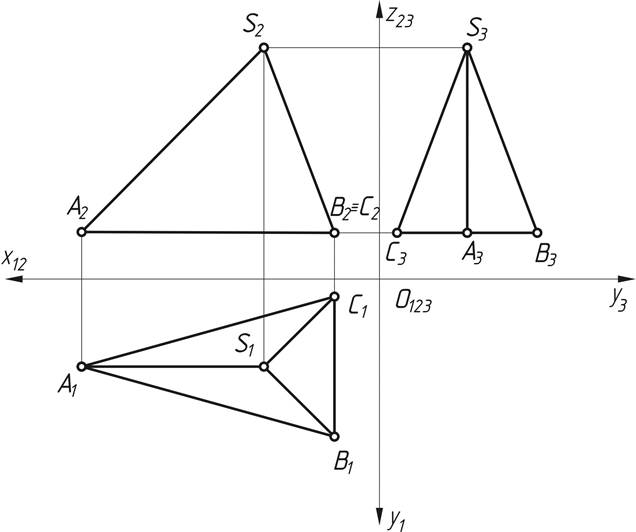
Рис.3. Построение комплексного чертежа пирамиды

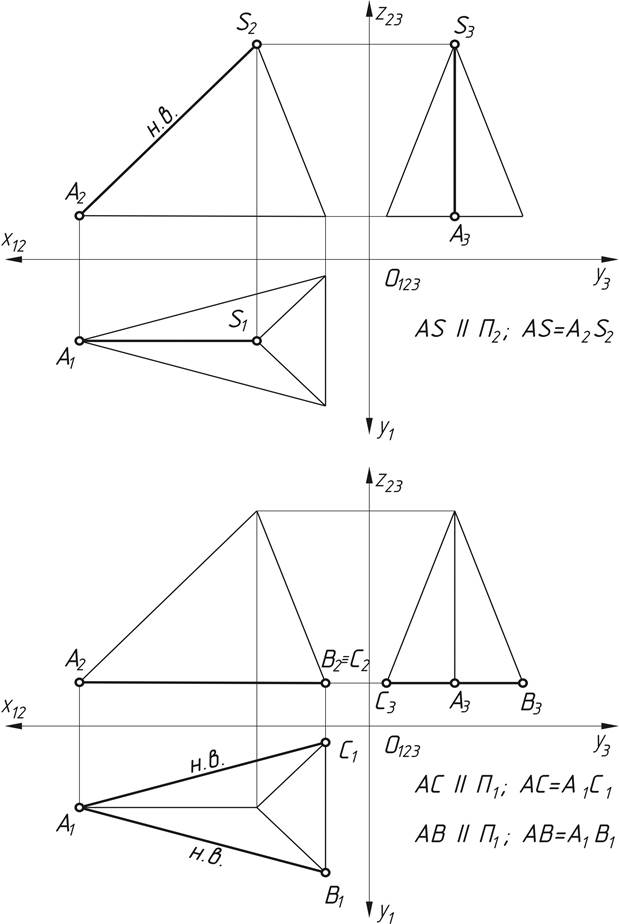
Рис.4. Определение натуральной величины ребер частного положе­ния

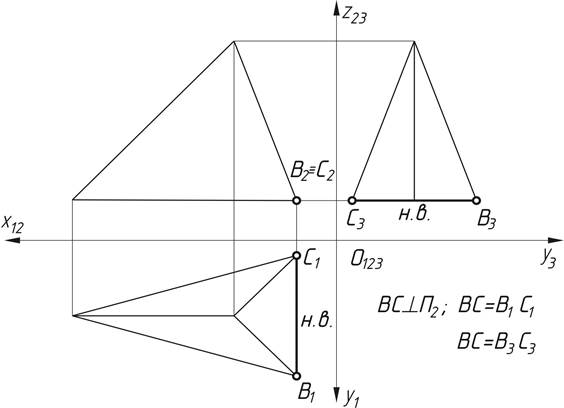
Рис.5. Определение натуральной величины ребра частного положения

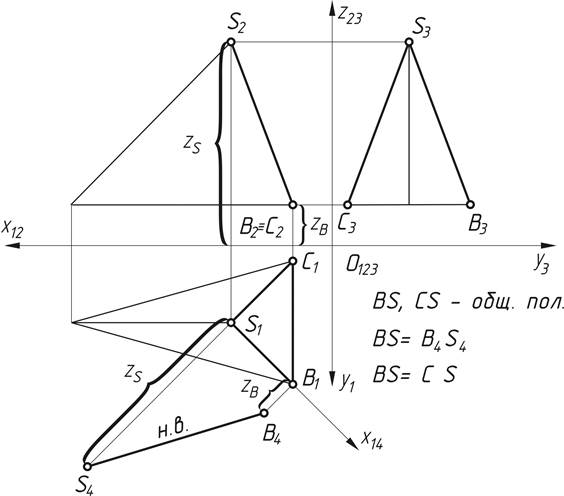
Рис.6.Построение натуральной величины ребра общего положения

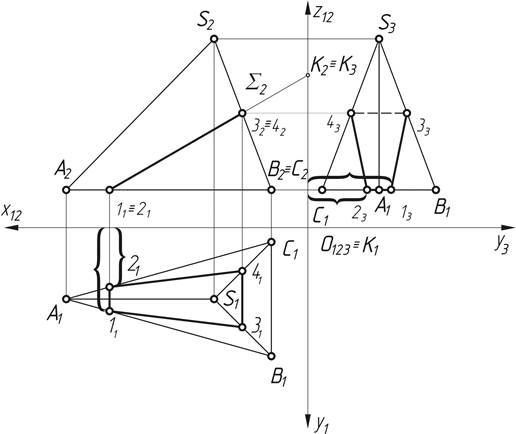
Рис.7. Построение проекций сечения пирамиды

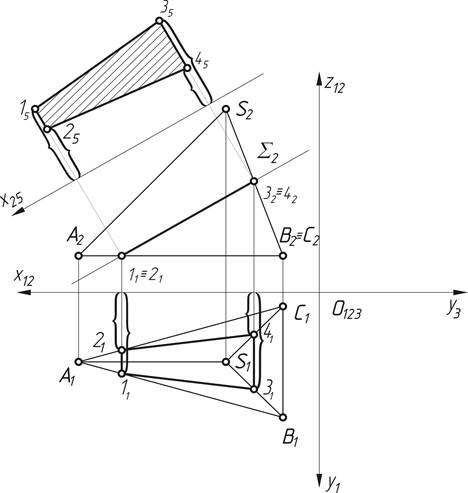
Рис.8. Построение натурального вида сечения пирамиды

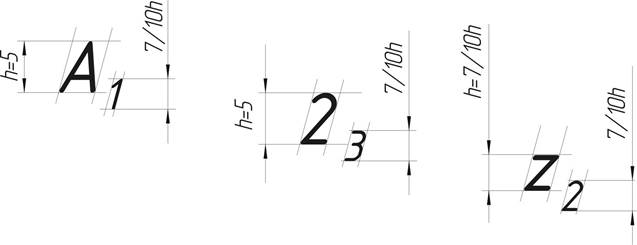
Рис. 9. Обозначение проекций точек, линий, осей

Рис.10. Вспомогательная сетка для надписей

Контрольные вопросы к защите

1. Может ли одна проекция фигуры обеспечить обратимость чертежа?

2. Что принимается за основные плоскости проекций?

3. Как может быть задана линия на комплексном чертеже?

4. Какие прямые являются прямыми общего положения, а какие - частного?

5. Сколько проекций необходимо для задания пря­мой общего положения на комплексном чертеже?

6. В чем состоит особенность изображения прямых уровня на комплексном чертеже?

7. Как называется прямая, одна из проекций которой изображается точкой?

8. Какими способами можно определить величину отрезков прямых общего положения на комплексном чертеже?

9. Как может быть задана плоскость на комплексном чертеже?

10. Какая плоскость называется плоскостью общего положения и по каким признакам ее можно отли­чить на комплексном чертеже?

11. Какие плоскости называются проецирующими, плос­костями уровня и по каким признакам их можно определить на комплексном чертеже?

12. Как можно определить натуральную величину плос­кой фигуры?

13. Какие разновидности криволинейных поверхностей?

14. Как могут быть заданы криволинейные поверхности на плоскостях проекций?

15. Каким образом могут быть созданы поверхности вращения?

16. Как проверить на комплексном чертеже, принадлежит ли точка поверхности вращения?

17. Как определить точки сечения прямой с телом вращения на комплексном чертеже?

18. Какие кривые можно получить, если плоскость пересекает прямой круговой цилиндр?

19. Какие кривые можно получить, если плоскость пересекает круговой конус?

20. В чем суть общего способа построения линии пересечения поверхностей?