Порядок выполнения лабораторной работы 5

1. Включить источник света.

2. Открыть крышку камеры 2 сахариметра и убедитесь, что трубка с раствором сахара вынута.

3. Вращением ручки 12 установить анализатор на темноту с одинаковым затемнением обеих половинок поля зрения, смотря в окуляр 10.

4. В окуляре прибора 10 наблюдать шкалу с нониусом (при правильной установке jдолжно быть равно 0).

5. Определить постоянную прибора следующим образом: поместить трубку с раствором сахара известной концентрации C₀ и известной длины L₀ (длину трубки принято выражать в дециметрах, измерьте самостоятельно) в камеру сахариметра, закрыть крышку и, вращая ручку 12, добиться того, чтобы обе половины поля зрения поляриметра были одинаково затемнены, как это было при начальной установке прибора.

6. По шкале окуляра 10 отсчитать угол поворота плоскости поляризации j₀.

7. Подставляя найденное значение j₀, известные значения C₀ и L₀ в формулу (5.1), вычислить постоянную прибора [α]. Измерения угла j₀ сделайте 5 раз и найти пять соответствующих значений для K. Из пяти значений определите среднее.

8. Взять другую трубку с раствором сахара неизвестной концентрации и, помещая в поляриметр, найие значение угла j₁.

9. Подставляя измеренное значение j₁, вычисленное среднее значение [α] и измеренное значение L₁ в формулу (5.1), определить концентрацию С₁.

Контрольные вопросы к лабораторной работе 5

1. Какие существуют способы получения плоскополяризованного света?

2. Какие вещества называются оптически активными?

3. Чем полутеневой метод определения угла поворота плоскости поляризации отличается от метода скрещенных поляризатора и анализатора?

4. Что такое двойное лучепреломление?

5. Чем отличается эллиптически поляризованный свет от линейно-поляризованного?

6. Как изготавливается призма Николя и в чем заключается принцип ее работы?

7. Какие материалы применяются для изготовления поляроидов?

8. Какие кристаллы называются положительными, а какие отрицательными?

9. Как устроен используемый в работе сахариметр и на чем основывается его принцип действия?

Рекомендуемая литература: [1], [4], [5], [8], [9], [10], [11].

Лабораторная работа 6

ИЗУЧЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ

Задание 6.1. Изучение дифракции на щели

Приборы и принадлежности: источник света – He-Ne лазер (l= 6328 Å); регулируемая щель; матовый экран; фотодиод, установленный на оптический столик; универсальный вольтметр.

Цель задания:ознакомление с явлениями дифракции Фраунгофера, экспериментальное исследование распределения освещенности при дифракции света на щели.

Краткая теория

Дифракцией называется явление огибания световыми волнами стоящих на их пути преград, соизмеримых с длиной волны. В зависимости от схемы наблюдения дифракционные явления условно разделяются на дифракцию Френеля и дифракцию Фраунгофера.

Дифракция Френеля наблюдается в расходящихся пучках лучей, когда на пути фронта световой волны располагается лишь непрозрачный экран, частично его загораживающий (рис. 6.1).

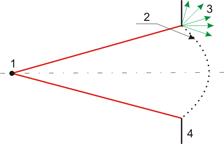
Рис. 6.1. Дифракция Френеля: 1 – источник света; 2 – фронт волны; 3 – дифрагировавшие лучи; 4 – преграда

Дифракция Фраунгофера наблюдается в параллельных лучах, причем рассматривается картина, возникающая в фокальной плоскости линзы, собирающей плоские световые волны, частично загороженные тем или иным непрозрачным экраном (рис. 6.2).

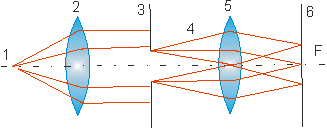
Рис. 6.2. Дифракция Фраунгофера: 1 – источник света; 2 – линза; 3 – щель; 4 – дифрагировавшие лучи; 5 – линза; 6 – фокальная плоскость

Рассмотрим дифракцию Фраунгофера на щели. Пусть монохроматический источник света 1 (рис. 6.3), находящийся в фокальной плоскости линзы 2, освещает щель 3. Выйдя из линзы, параллельный пучок лучей падает на щель 3, расположенную перпендикулярно плоскости рисунка.

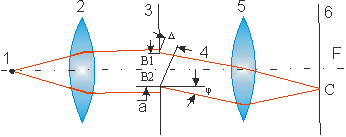
Рис. 6.3. Схема к расчету дифракции на щели: 1 – источник света; 2 – линза; 3 – щель; 4 – дифрагировавшие лучи; 5 – линза; 6 - фокальная плоскость

Каждая точка волнового фронта, достигшего щели, согласно принципу Гюйгенса, является источником вторичных волн, распространяющихся во все стороны. Эти волны называются дифрагировавшими, а углы, образованные соответствующими им лучами с первоначальным направлением, называются углами дифракции. Если ширина щели соизмерима с длиной l в пределах нескольких порядков, то на экране 6, помещенном в фокальной плоскости линзы 5, наблюдается дифракционная картина, представляющая собой дифракционное изображение щели 3.

Найдем освещенность в точке С (рис. 6.3). В этой точке соберутся лучи, дифрагировавшие под углом j. Для определения освещенности в точке С необходимо вычислить суммарную амплитуду всех дифрагировавших волн, пришедших в эту точку. Для этого разобьем волновой фронт B₁В₂ на зоны в виде узких полосок одинаковой ширины, параллельных краям щели, и припишем колебаниям, идущим от каждой зоны, амплитуду 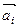. Так как световые волны, идущие от каждой зоны до точки С, проходят пути разной длины, то они придут в эту точку с разными фазами. Положим начальную фазу колебаний, приходящих в точку С от крайней нижней зоны (луч В₂С), равной нулю. Тогда начальная фаза колебаний, приходящих в точку С от каждой следующей зоны, будет постепенно увеличиваться до некоторого значения d. Графически вектор амплитуды 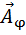суммарного колебания равен
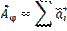и изобразится замыкающей ломаной линией, образованной векторами .

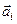Если разность хода лучей B₁C и В₂С равна D, то, как известно, начальная фаза d будет связана с разностью хода лучей D соотношением

,

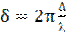где l — длина волны падающего света; с другой стороны (рис. 6.3)

D = b sinj,где b — ширина щели. Следовательно,
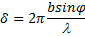(6.1)

Освещенность в точке С будет различной при различных значениях d, а следовательно, и углах дифракции j.

В главном фокусе F линзы 5 угол j = 0. Ему соответствует d=0, это означает, что все векторы направлены в одну сторону, как показано на графике (рис. 6.4, а). В этом случае амплитуда результирующих колебаний 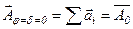является максимальной. Таким образом, в центре дифракционной картины получается максимальная освещенность. При d = 2p ломанная линия, образованная векторами 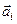, замыкается (рис. 6.4).

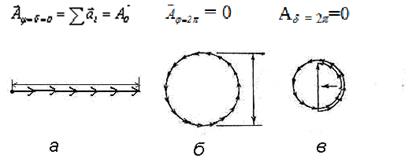
Рис. 6.4. Расчет дифракционной картины методом графического сложения амплитуд: а-d = 0; б- d = 2p; в-d = 3p

результирующих колебаний 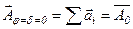является максимальной. Таким образом, в центре дифракционной картины получается максимальная освещенность. При d = 2p ломанная линия, образованная векторами 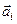, замыкается (рис. 6.4). Этому соответствует минимальное значение освещенности, равное нулю, так как 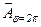= 0. Положение этого минимума определяется по формуле (6.1) значением угла j, удовлетворяющего условию, bsinj=l или sinj = l/b.

Очевидно, что такой же минимум расположится по другую сторону от центрального максимума при sinj = –l/a. При этом d = – 2p. Результирующая амплитуда 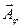окажется равной 0 каждый раз, когда d = 2kp, где k — целое число. Между двумя соседними минимумами расположатся относительные максимумы. Очевидно, 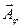будетмаксимальной каждый раз, когда d = ± p; ±3p;...; ±(2k+1)p(рис. 6.4, в, г), а следовательно, при

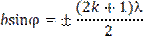; k = 1,2,3… (6.2)

Освещенность в этих максимумах, пропорциональная квадрату амплитуды, будет тем меньше, чем больше угол j.

Окончательно получаем такой вид дифракционной картины от одной щели (рис. 65): в центре (j = 0) светлая полоса – максимум освещенности, а по обе стороны расположены вторичные, относительно слабые, максимумы, их относительная освещённость указана на рис. 6.5. Эти максимумы разделены минимумами, освещенность которых равна нулю.

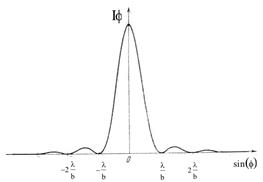
Рис. 6.5. Зависимость относительного распределения освещенности дифракционной картины от sin j при дифракции на щели шириной b

Положение минимумов определяется условием

bsinφ=±kl; k = 1,2,3 (6.3)

Следует заметить, что при смещении щели B₁B₂ параллельно самой себе в той же плоскости дифракционная картина не меняется, положения максимумов и минимумов и относительное распределение освещенности остаются неизменными.