Построения угловых сумм
ВВЕДЕНИЕ
В разделе 6.1 мы узнали, что двумерное преобразование Фурье - это один из способов разложения волнового поля на его плосковолновые составляющие, каждая из которых имеет уникальную частоту и распространяется под определенным углом к вертикали. В этой главе рассматривается область параметра луча и другой способ разложения волнового поля на плосковолновые составляющие. Это разложение волнового поля (например, выборки ОПВ) можно получить, применив линейное приращение (LMO) и суммирование амплитуд по оси удалений "взрыв-прибор". Такая процедура носит название углового суммирования (slant stacking). В основе углового суммирования лежит предположение о горизонтально-слоистом разрезе. Общепринятая обработка выполнятся в координатах "средняя точка-вынос". При угловом суммировании ось выносов замещается осью параметров луча p. Параметр луча представляет собой величину, обратную горизонтальной фазовой скорости. Семейство трасс с диапазоном значений p называется выборкой угловых сумм (slant stack gather).
Создано несколько методик обработки в координатах "средняя точка-параметр луча". В качестве примеров можно привести интерполяцию между трассами (Раздел 7.2), фильтрацию наклонов (Раздел 7.4),, подавление кратных волн (Раздел 7.5), обращение преломленной волны (refraction inversion) (Приложение Е), миграцию и скоростной анализ. Taner (1977) первым ввел координаты "средняя точка-параметр луча". Он рассмотрел использование сумм плоских волн для интерпретации, когда несколько разрезов с постоянным p накладываются друг на друга в ограниченном диапазоне величин p с целью улучшения вступлений, обусловленных наклонными поверхностями. Позднее были исследованы другие методы обработки, такие как миграция (Ottolini, 1982) и скоростной анализ (Schultz и Claerbout, 1978; Diebold и Stoffa, 1981а; Gonzalez-Serrano, 1982). Alam и Losocki (1981а) и Alam и Austin (1981b) обсудили возможное применение соответственно при интерполяции между трассами и подавлении кратных волн. Clayton и McMechan (1981) разработали метод обращения поля преломленных волн, который включает продолжение вниз в области наклонной суммы. McMechan и Yedlin (1981) разработали метод получения кривых фазовой скорости для диспергированных волн с помощью преобразования угловых сумм. Основываясь на продолжении вниз выборки угловых сумм, Schultz (1982) разработал оценку интервальных скоростей.
Исследуем физические аспекты построения выборки угловых сумм, которая обычно упоминается как тау-p-выборка или p-выборка. Каждая трасса в этой выборке представляет плоскую волну, которая распространяется под определенным углом к вертикали. В реальных условиях при взрыве заряда ВВ энергия распространяется под всеми углами (рис.7.1). Отраженная энергия поступает на различные группы сейсмоприемников под различными углами, поскольку между точками взрыва и приема существует удаление. Чем больше удаление взрыв-прибор или чем меньше глубина отражающей поверхности, тем более наклонным является восходящий волновой фронт.
Чтобы было легче определить схему построения выборки угловых сумм, сначала рассмотрим, как могут формироваться плоские волны. На рис.7.2 показан профиль точечных источников. Допустим, что все заряды на этом профиле взрываются одновременно, и каждый из них формирует сферическое волновое поле. На некотором расстоянии от поверхности земли сферические волновые фронты накладываются друг на друга, и получается плоская волна, которая распространяется вертикально вниз. Эта плоская волна отражается от границы раздела и регистрируется сейсмоприемником на поверхности земли. Такие типы источников как Геофлекс (Geoflex - торговая марка Imperial Chemical Industries) и Примакорд (Primacord - торговая марка Ensign-Bickford) можно представить как короткопрофильные источники.
Плоскую волну, которая распространяется под нужным углом к вертикали, можно сформировать, используя такой же профиль точечных источников (рис.7.3). Для этого источники должны быть приведены в действие последовательно, начиная с одного конца профиля при одинаковых временных задержках. При взрыве определенного точечного источника волновой фронт, сформированный предыдущим источником, уже пройдет некоторое расстояние. При наложении сферических волновых фронтов, сформированных различными источниками, получается наклонный плоский волновой фронт (рис.7.3). Эта плоская волна распространяется, отражается от границы раздела и регистрируется сейсмоприемником на поверхности.
Величиной наклона волнового фронта (или углом распространения плоской волны) можно управлять. Рассмотрим геометрические построения на рис.7.4. К моменту, когда волновой фронт, сформированный источником S1, достигнет точки А в разрезе, точечный источник S2 должен быть взорван так, чтобы получился нужный угол. Определим расстояние между S1 и S2 как Dх, а скорость, с которой в среде распространяется волна, - как v. Если волновой фронт проходит от S1 до А за время Dt, угол наклона q плоской волны можно определить как
| sinq = vDt/Dx | (7.1) |
Точка, в которой произошел взрыв, должна перемещаться со скоростью Dx/Dt=v/sinq в горизонтальном направлении, а точечный источник S2 должен быть взорван при достижении волновым фронтом от S1 точки А. Скорость, с которой должна перемещаться точка расположения источника, называется горизонтальной фазовой скоростью (horizontal phase velocity).
Из рис.7.2 и 7.3 следует, что плоская волна, которая распространяется под углом к вертикали, может быть сформирована:
1. 1. Путем размещения точечных источников на поверхности земли
2. 2. Путем последовательного инициирования точечных источников с задержкой во времени
3. 3. Путем суперпозиции откликов, имеющих форму сферических волновых фронтов
Отклик, полученный в результате суперпозиции, регистрируется одним сейсмоприемником (рис.7.3) и имеет форму плоской волны, которая отражается от поверхности. Суперпозиция означает суммирование по оси источников для данной точки приема. Используя принцип взаимности, суммирование можно также выполнить по оси точек приема для данной точки взрыва.
Приведенные выше рассуждения показывают, каким образом выборка ОПВ, рассматриваемая как поле одной волны, может быть разложена на плосковолновые составляющие. Заменяя ось точек взрыва на рис.7.4 осью точек приема, получаем геометрию луча, показанную на рис.7.5. Временная задержка, ассоциированная с плоской волной, которая распространяется под углом q к вертикали, имеет вид:
| Dt = (sinq/v)Dx | (7.2) |
Согласно закону Снеллиуса, значение sinq/v, которое представляет собой величину, обратную горизонтальной фазовой скорости, является постоянным вдоль луча в слоистой среде (рис.7.6). Эта постоянная называется параметром луча p. Перепишем ур. (7.2):
| Dt = pDx | (7.3) |
Угол распространения плоской волны определяется величиной p.p=0 соответствует плоской волне, распространяющейся по вертикали. Если задать p и скоростную модель для слоистого разреза, можно построить семейство лучей, ассоциированных с определенной величиной p (рис.7.7). Плоская волна, которая распространяется в слоистой среде, называется волной Снеллиуса (Claerbout, 1978). Плоская волна этого типа изменяет направление распространения на границе каждого слоя согласно закону Снеллиуса (рис.7.6). Для одного значенияp сигнал регистрируется на нескольких удалениях взрыв-прибор (рис.7.7). В общем случае приемники на всех удалениях регистрируют плоские волны со многими величинами p. Чтобы разложить выборку общего выноса на плосковолновые составляющие, все амплитуды в выборке должны быть суммированы по нескольким наклонным лучам, каждый из которых характеризуется общей временной задержкой, определенной уравнением (7.3).
Мы рассмотрели разложение волнового поля выборки ОПВ на плосковолновые составляющие. Пока отсутствует наклон отражающих поверхностей, годографы в выборках ОПВ и ОГТ неразличимы (рис.7.8). Поскольку выборка ОГТ не является отдельным волновым полем, может показаться, что разложение на плосковолновые составляющие нельзя применить к выборкам ОГТ. Однако эквивалентность выборок ОГТ и ОПВ в горизонтально-слоистой среде дает основание для применения разложения на плосковолновые составляющие к обоим типам выборок.
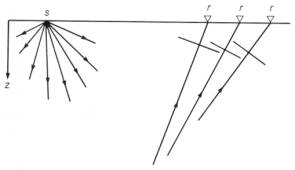 Рис.7.1 Сейсмический источник формирует волны, распространяющиеся во всех направлениях; такие волны регистрируются сейсмоприемниками, расположенными в различных точках. Рис.7.1 Сейсмический источник формирует волны, распространяющиеся во всех направлениях; такие волны регистрируются сейсмоприемниками, расположенными в различных точках. | 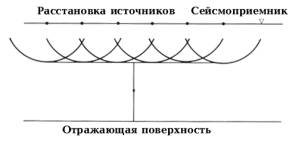 Рис.7.2 Вертикально падающая волна формируется путем одновременного инициирования нескольких источников. Рис.7.2 Вертикально падающая волна формируется путем одновременного инициирования нескольких источников. |
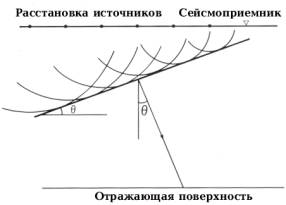 Рис.7.3 Плоская волна, распространяющаяся под углом q к вертикали, формируется путем инициирования нескольких источников (начиная с левого) с определенным временным интервалом. Рис.7.3 Плоская волна, распространяющаяся под углом q к вертикали, формируется путем инициирования нескольких источников (начиная с левого) с определенным временным интервалом. | 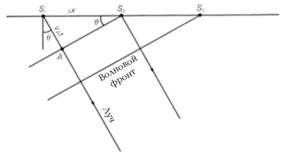 Рис.7.4 Расчет временного интервала инициирования источников (S) с целью формирования плоской волны на рис.7.3. Рис.7.4 Расчет временного интервала инициирования источников (S) с целью формирования плоской волны на рис.7.3. |
ПОСТРОЕНИЯ УГЛОВЫХ СУММ
Синтезирование плоских волн путем суммирования амплитуд в области выносов вдоль наклонных лучей обычно выполняется в два шага. Сначала к данным применяется поправка за линейное приращение (LMO) путем преобразования координат (Claerbout, 1978):
| t = t – px, | (7.4) |
где p - параметр луча, х - вынос, t - полное время пробега, t - линейно смещенное время. После применения поправки за линейное приращение отражение, наклонное на входе, становится горизонтальным. Далее, данные суммируются по оси выносов для получения:
S(p, t) = 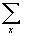 P(x, t + px) P(x, t + px) | (7.5) |
Здесь S(p, t) представляет плоскую волну с параметром луча p = sinq/v. Повторяя операцию ввода поправки за линейное приращение для различных величин p и суммирование [ур.(7.5)], можно построить полную выборку угловых сумм (или p-выборку), которая включает все составляющие наклона в первоначальных данных.
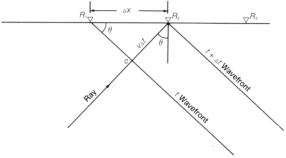 | Рис.7.5 Принцип взаимности, примененный к геометрическому построению на рис.7.4 для замещения источников (S) сейсмоприемниками (R) |
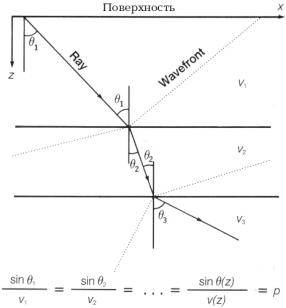 Рис.7.6 Если параметр луча p определен, можно построить луч в горизонтально-слоистой модели разреза с известной скоростной функцией Рис.7.6 Если параметр луча p определен, можно построить луч в горизонтально-слоистой модели разреза с известной скоростной функцией | 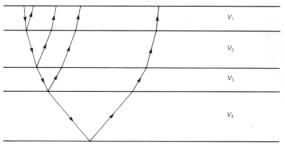 Рис.7.7 Некоторые лучи для данной величины p, соответствующей одной трассе в плоскости (p, t) Рис.7.7 Некоторые лучи для данной величины p, соответствующей одной трассе в плоскости (p, t) 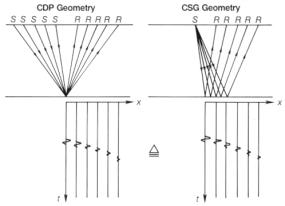 Рис.7.8 Лучи и времена пробега, ассоциированные с геометрией ОГТ и ОПВ Рис.7.8 Лучи и времена пробега, ассоциированные с геометрией ОГТ и ОПВ |
Угловая сумма и разложение волнового поля на плосковолновые составляющие не различаются между собой. Treitel и др. (1982) выполнил математический анализ процесса разложения на плосковолновые составляющие и сделал различие между общепринятой угловой суммой, рассмотренной здесь, и угловой суммой в собственном смысле. Общепринятая угловая сумма дает точное разложение на плосковолновые составляющие, когда мы имеем дело с линейными источниками; угловая сумма в собственном смысле дает точное разложение на плосковолновые составляющие, когда мы имеем дело с точечными источниками. Угловая сумма в собственном смысле формируется с использованием тех же шагов, которые рассмотрены для общепринятой угловой суммы; исключением является то, что свертка линейно смещенного волнового поля с оператором фильтра выполняется перед суммированием. Этот оператор вносит поправки за трехмерные эффекты, преобразуя волновое поле, полученное по точечному источнику, в волновое поле, полученное по линейному источнику. Пока дело касается кинематики, два типа углового суммирования являются эквивалентными. Они различаются только при обработке амплитуд (Treitel, персональное сообщение).
Схематическое описание распределения плоской волны с помощью ур.(7.4) и (7.5) показано на рис.7-9. Начнем с суммирования амплитуд в области удалений взрыв-прибор по горизонтальной траектории, p = 0. Эта линия пересекает годограф отраженной волны в окрестности точки А (вершины). Точка А попадает в точку А` на плоскости (p, t). При наклоне линии суммирования пересечение с годографом происходит в точке В, которая попадает в точку В`. Основной вклад в сумму вдоль наклонной траектории поступает в область точки касания В. Эта область называется зоной Френеля. Чем выше скорость и глубже отражения, тем шире зона Френеля. Фактически суммирование в ур.(7.5) может быть ограничено зоной Френеля. Траектория суммирования характеризуется небольшим наклоном: это
p = 1/v, т.е. асимптота гиперболы. Такая траектория соответствует лучам, отклоняющимся от вертикали на 90 град. Энергия вдоль асимптоты попадает в С` на оси p.При использовании описанного выше распределения гиперболические траектории в области (x, t) становятся эллиптическими траекториями в области (p, t) (Schultz и Claerbout, 1978; см. упр.7.1). В реальных условиях мы никогда не регистрируем годограф бесконечной протяженности и трассу с нулевым выносом. Следовательно, эллиптическая траектория в области наклонного суммирования никогда не бывает полной от A` до С`.
На рис.7.10 показан более сложный случай. Докритические отражения А и D (т.е. отражения с углом падения меньше критического) попадают в область пониженных значенийp, тогда как закритические отражения С попадают в область повышенных значений p. В идеальном случае линейное отражение в области удаления взрыв-прибор, такое как вступление преломленной волны В, становится точкой в области угловой суммы. И наоборот, линейное отражение в области угловой суммы становится точкой в области удаления взрыв-прибор (упр.7.2).
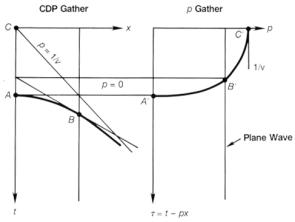 Рис.7.9 Гипербола на выборке ОГТ становится эллипсом на p-выборке Рис.7.9 Гипербола на выборке ОГТ становится эллипсом на p-выборке | 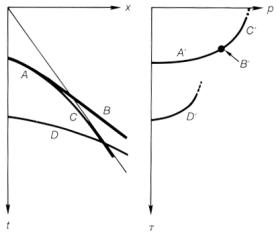 Рис.7-10 Различные вступления на выборке ОГТ распределяются в соответствующую p-выборку. Отражения A,B,C,D распределяются в A`,B`,C`,D` Рис.7-10 Различные вступления на выборке ОГТ распределяются в соответствующую p-выборку. Отражения A,B,C,D распределяются в A`,B`,C`,D` |
На рис.7.11 показан пример полевых данных, содержащих, в основном, отражения от дна и многократные отражения в тонком слое. Кроме отражений от дна W имеются два хорошо различимых отражения Р1 и Р2. Кратные отражения распределяются вдоль эллиптических траекторий, сходящихся при p = (1/1500)с/м (величина, обратная скорости в воде). Пример полевых данных, содержащих линейные отражения, показан на рис.7.12. Обратите внимание на интенсивные амплитуды на выборке угловых сумм, которые соответствуют канальным волнам, наблюдаемых в данных выноса. В обоих примерах полевых данных выборки угловых сумм были созданы с использованием только положительных величин p. Следовательно, энергия, рассеянная в обратном направлении в данных выноса на рис.7.12, не представлена в выборке угловых сумм.
Перейдем к взаимосвязям между различными областями, которые используются в обработке сейсмических данных. Рассмотрим отражение от наклонной границы в ограниченной полосе пропускания в области выносов (t, x), как показано на рис.7.13. Величина выноса изменяется от 250 до 5000м при шаге между трассами 50м. Это отражение распределяется вдоль хорошо различимой радиальной линии в f-k-области (w, kx). Наклон радиальной линии связан с горизонтальной фазовой скоростью соотношением:
| w/kx = v/sinq | (7.6) |
Подставим p = sinq/v, чтобы найти взаимосвязь между переменными в области преобразования:
| kx = pw | (7.7) |
На рис.7.13 также показано распределение отражения от наклонной границы в области угловой суммы. Одномерное преобразование Фурье трасс угловой суммы в направлении времени дает амплитудный спектр (p, w), который также показан на рис.7.13. Эта плоскость описывает зависимость горизонтальной фазовой скорости от частоты и используется при анализе канальных волн (Раздел 7.3). Энергия вдоль радиального направления АА` на плоскости (w, kx) эквивалентна энергии вдоль вертикального направления ВВ` на плоскости (p, w).
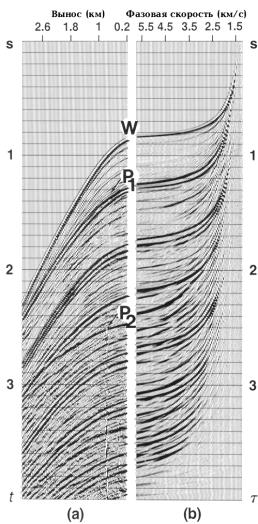 Рис.7.11 (а) Выборка ОПВ, содержащая интенсивные кратные волны; (b) соответствующая p-выборка. Горизонтальная ось в b представляет собой горизонтальную фазовую скорость (1/p). (Данные Shell и Esso). Рис.7.11 (а) Выборка ОПВ, содержащая интенсивные кратные волны; (b) соответствующая p-выборка. Горизонтальная ось в b представляет собой горизонтальную фазовую скорость (1/p). (Данные Shell и Esso). 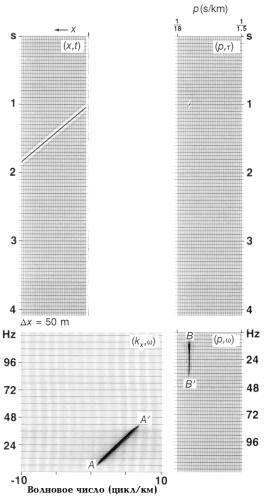 Рис.7.13 Одно отражение от наклонной границы в различных областях. Рис.7.13 Одно отражение от наклонной границы в различных областях. | 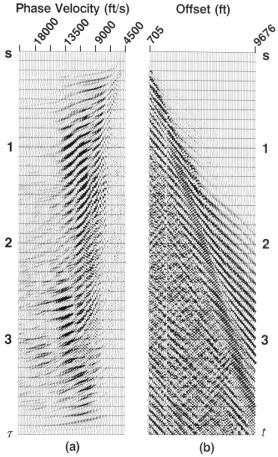 Рис.7.12 (b) Выборка ОПВ; (а) ее угловая сумма. Горизонтальная ось в b представляет собой горизонтальную фазовую скорость (1/p). Рис.7.12 (b) Выборка ОПВ; (а) ее угловая сумма. Горизонтальная ось в b представляет собой горизонтальную фазовую скорость (1/p). 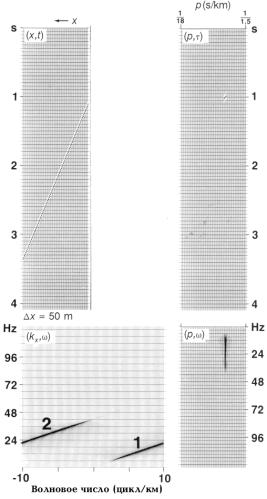 Рис.7.14 Пространственно неоднозначное отражение от наклонной границы в различных областях. Рис.7.14 Пространственно неоднозначное отражение от наклонной границы в различных областях. |
На рис.7.14 показана пространственно неоднозначная составляющая наклона. Циклический возврат (wraparound), наблюдаемый в плоскости (w, kx), является результатом неадекватной пространственной дискретизации сигнала. Обратите внимание, что составляющие с пространственной неоднозначностью и без нее (участки соответственно 1 и 2) попадают на одну p-трассу. Мы ожидаем, что пространственно неоднозначная часть попадет на ряд отрицательных p-трасс. Однако, диапазон частот с побочной составляющей (21-42Гц) будет отсутствовать на плоскости (p, w), в которую были включены только положительные величины p. На рис.7.14 показан случай одного наклона; восстановление диапазона наклонов рассмотрено на рис.7.17.
После выполнения определенного процесса в области наклонных сумм используется обратное распределение для восстановления данных в области выносов. Thorson (1978) предоставил детали процедуры восстановления. Для надлежащего восстановления амплитуд перед обратным распределением применяется ро-фильтрация. Это выполняется путем умножения амплитудного спектра каждой трассы угловой суммы на абсолютную величину частоты. Данное действие, в некоторой степени, аналогично дифференцированию волнового поля перед суммированием, которое включено в интегральную формулировку миграции [ур.(4.5)].
На рис.7.15 показана блок-схема обработки наклонной суммы.
 | На рис.7.16 можно видеть синтетическую выборку удалений взрыв-прибор, соответствующую угловую сумму и восстановленную выборку удалений взрыв-прибор без какого-либо примененного процесса за исключением ро-фильтрации. Распределение x в p носит обратимый характер (Thorson, 1978). Причиной появления полосок (СР) на выборке угловых сумм является конечная длина косы. Введение переходной зоны на обеих сторонах выборки выносов помогает подавить эти эффекты конечной длины косы. В процессе восстановления выборки (x, t) мы не должны использовать тот же интервал между трассами, который был взят для первоначальной выборки (x, t). Рассмотрим синтетическую выборку на рис.7.17а. |
Двумерный амплитудный спектр показывает, что частоты более 48Гц являются пространственно неоднозначными (рис.7.17b).Эта выборка может быть распределена в область угловых сумм (рис.7.17с) и восстановлена с применением меньшего интервала между трассами (рис.7.17d). Первоначальный интервал равен 25м; в восстановленной выборке он составляет 12.5м. Двумерный амплитудный спектр выборки с интерполяцией между трассами показывает отсутствие пространственно неоднозначных частот (рис.7.17е). Тем не менее, обратите внимание на пропущенную высокочастотную энергию при превышении 60Гц. Эта энергия в основном распределена вдоль годографа прямой волны во входной выборке (рис.7.17а) и отсутствует в выходной выборке (рис.7.17d). Мы видим, что восстановление может быть успешным даже для пространственно неоднозначных данных при условии изменения углов наклона в узких пределах.
