Момент инерции маховика

Таблица 2.1

Nп	pa	ab	pb	de	ps2	ps3	ps4	pe	pm	pk	pn
									-21
									-15
									-24
									-10
								-11		-2	-14
								-24		-5	-30
								-47		-13	-55
								-75		-24	-78
								-71	-5	-25	-67
								-65	-28	-25	-57
								-46	-70	-19	-39

Прикладываем в точке (е) силу полезного сопротивления Q и силу тяжести G₅, в точках s₂, s₃, s₄ силы тяжести G₂, G₃, G₄ соответственно.

Приведенный момент этих сил определяется по формуле

Mc = (Q×<pe> ± G₂×<pm> ± G₃×<pk> ± G₄×<pn> ± G₅×<pe>)×OA/<pa>, Нм,

где <pe>, <pm>, <pk>, <pn> - плечи сил относительно полюса плана, мм.

Например, в положении 1

Mc = (150×74 - 58,86×15 + 98,1×26 + 58,86×69 + 49,05×74)×0,1/40 = 51,177 Нм.

Значения приведенного момента сил заносим в табл. 2.2.

2.2. Приведенный момент инерции

Приведенный момент инерции определяется как момент, которым должен обладать кривошип относительно своей оси вращения, чтобы его кинетическая энергия равнялась кинетической энергии механизма.

Таким образом, приведенный момент инерции нашего механизма

Jп = 2T/w₁² = Js₁ + m₂×(Vs₂/w₁)² + Js₂×(w₂/w₁)² + Js₃×(w₃/w₁)² + m₄×(Vs₄/w₁)² + Js₄×(w₄/w₁)² + m₅×(Vs₅/w₁)² , кгм².

Отношения скоростей могут быть найдены по данным таблицы 2.1:

Vs₂/w₁ = OA×<ps₂>/<pa>, м;

w₂/w₁ = OA×<ab>/<pa>/AB;

w₃/w₁ = OA×<pb>/<pa>/BC;

Vs₄/w₁ = OA×<ps₄>/<pa>, м;

w₄/w₁ = OA×<de>/<pa>/DE;

Vs₅/w₁ = OA×<pe>/<pa>, м.

Таблица 2.2

Nп	Mc	Jп	DT	w	w(м)
	30,924	0,305		18,339	19,935
	51,177	0,646	-11,467	11,104	18,578
	27,523	0,356	-22,045	12,818	19,337
	11,812	0,190	-22,316	17,464	19,946
	5,148	0,135	-16,730	22,627	20,272
	3,159	0,129	-8,878	25,643	20,449
	4,606	0,159	-0,884	25,180	20,482
	7,180	0,220	6,057	22,833	20,372
	14,395	0,299	10,435	20,319	20,151
	27,291	0,353	9,548	18,566	19,935
	34,218	0,307	3,472	18,888	19,992
	12,358	0,153	1,305	26,220	20,549

Приведем пример вычисления приведенного момента инерции механизма в положении 1:

Vs₂/w₁ = 0,1×42/40 = 0,105 м;

w₂/w₁ = 0,1×65/40/0,35 = 0,464;

w₃/w₁ = 0,1×67/40/0,2 = 0,838;

Vs₄/w₁ = 0,1×70/40 = 0,175 м;

w₄/w₁ = 0,1×14/40/0,35 = 0,1;

Vs₅/w₁ = 0,1×74/40 = 0,185 м.

Jп₁ = 0,1 + 6×0,105² + 0,09×0,464² + 0,15×0,838² + 6×0,175² + 0,09×0,1² + 5×0,185² = 0,646 кгм².

Значения приведенного момента инерции для всех положений сведены в таблицу 2.2. По этим значениям строим диаграмму приведенного момента инерции (Jп-j), выбирая масштабный коэффициент

m_J = 0,00538 кгм²/мм.

Диаграмму (Jп-j) строим повернутой на 90 градусов для удобства выполнения последующих графических операций.

2.3. Диаграммы приведенных моментов сил, работ и изменения кинетической энергии

По данным таблицы 2.2 строим диаграмму приведенного момента сил сопротивления в зависимости от угла поворота кривошипа (Mc - j). Предварительно выбираем масштабные коэффициенты осей

mм = 0,853 Нм/мм;

m_j = 0,035 рад/мм (2 град/мм).

Графическим интегрированием диаграммы (Мс-j) получаем диаграмму работы сил сопротивления (Ас-j). Методика графического интегрирования изложена в [1].

Масштабный коэффициент оси работ

m_A = m _j × mм × <po> = 0,035 × 0,853 × 30 = 0,893 Дж/мм,

где <po> - расстояние от центра координат до полюса интегрирования.

На вал кривошипа кроме приведенного момента сил сопротивления действует движущий момент. В случае «мягкой» характеристики двигателя (двигатель внутреннего сгорания) этот момент имеет постоянную величину (М_дв = const). Диаграмма работы постоянного момента представляет линейную функцию, имеющую одинаковые значения с работой сил сопротивления в начале и в конце цикла. Соединяем прямой начало и конец диаграммы (Ас-j) и получаем диаграмму работы движущего момента (А_дв-j).

Графическим дифференцированием диаграммы (А_дв-j) строим диаграмму движущего момента (М_дв-j), которая представляет собой горизонтальную прямую. Величина движущего момента

М_дв = <M_дв> × mм = 23 × 0,853 = 19,62 Нм.

Как известно изменение кинетической энергии механической системы равно алгебраической сумме работ действующих на систему внешних сил. Поэтому диаграмму изменения кинетической энергии механизма (DT - j) строим в виде разности ординат работ движущего момента и момента сил сопротивления, т.е.

<DT> = <А_дв> - <Ас>.

2.4. Расчет угловых скоростей кривошипа (без маховика)

Расчет угловых скоростей выполняем численным способом. Для этого используем уравнение кинетической энергии механизма в дискретном виде (индекс звена 1 у угловой скорости кривошипа опущен):

Jп_iw_i²/2 – Jп₀w₀²/2 = DT_i, i = 1..12.

Отсюда

w_i = Ö[(2 DT_i + Jп₀w₀²)/Jп_i], i = 1..12.

Начальную величину угловой скорости w₀ подбираем итерационным путем, используя Excel/подбор параметра, из условия ( 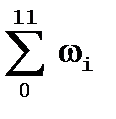)/12 » w_ср, где w_ср – заданное значение угловой скорости кривошипа 1 (см.Данные). Определяем коэффициент неравномерности движения

d = (w_max - w_min)/w_ср = (26,22-11,104)/20 = 0,756 > 0,1.

Поскольку величина d превышает заданное значение (d = 0,1), то выполняем расчет маховика методом Виттенбауэра.

2.5. Диаграмма Виттенбауэра. Момент инерции маховика

Строим диаграмму Виттенбауэра (DT-Jп) способом графического исключения угла (j) из диаграмм (DT-Jп) и (Jп-j). При этом масштабные коэффициенты осей DT и Jп сохраняются.

К диаграмме Виттенбауэра проводим касательные под углами Y_max и Y_min, значения которых:

tgY_max = m_J×w_ср²×(1+d)/(2×m_DT) =

= 0,00538×20²×(1+0,1)/(2×0,893) = 1,326; Y_max = 53 град;

tgY_min = m_J×w_ср²×(1-d)/(2× m_DT) =

= 0,00538×20²×(1-0,1)/(2×0,893) = 1,085; Y_min = 47,3 град.

Касательные отсекают на оси DT отрезок <kl> = 107 мм.

Момент инерции маховика

Jм = <kl>×m_DT /(w_ср²×d) = 107×0,893/(20²×0,1) = 2,385 кгм².

Повторяем итерационный расчет угловых скоростей кривошипа численным способом с учетом момента инерции маховика по уравнению:

w^(м)_i = Ö[(2 DT_i + (Jм+Jп₀)w^(м)₀²)/(Jм+Jп_i)], i = 1..12.

Определяем коэффициент неравномерности движения с маховиком

d^(м) = (w^(м)_max-w^(м)_min)/w_ср = (20,549-18,578)/20 = 0,099 » 0,1.