Что следует из соответствующего свойства несобственного интеграла
Заметим, что если интегралы справа абсолютно сходятся в разных полуплоскостях 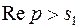 и
и 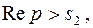 то интеграл слева сходится в их общей части.
то интеграл слева сходится в их общей части.
Разумеется, теорема линейности справедлива для любого конечного числа слагаемых:
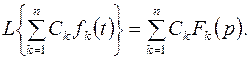
В частности, при 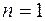 имеем
имеем 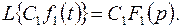
3.1.2. Изображения простейших функций. В качестве применения теоремы линейности найдем изображения функций 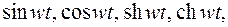 где
где  действительное число.
действительное число.
По формуле Эйлера имеем
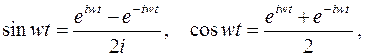
Применяя свойство линейности (3.1), где положено 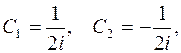 и пользуясь формулой – соответствием (1.3), где следует принять
и пользуясь формулой – соответствием (1.3), где следует принять 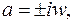
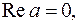 получим
получим
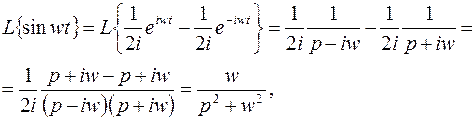
если 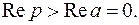
Аналогично получим
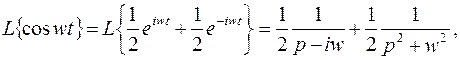
если 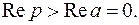
Итак,
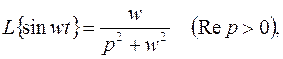 (3.2)
(3.2)
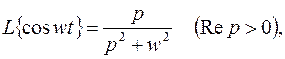 (3.3)
(3.3)
Исходя из определения гиперболических функций
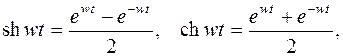
найдем их изображения, пользуясь (3.1) и (1.3):
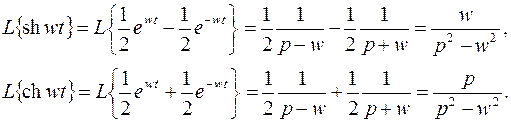
Это справедливо, когда одновременно выполняется  и
и 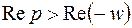 , т.е. когда
, т.е. когда 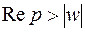 .
.
Итак,
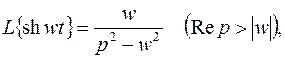 (3.4)
(3.4)
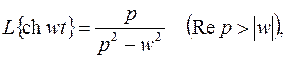 (3.5)
(3.5)
3.1.3. Теорема подобия.Если 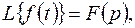 то для любого числа
то для любого числа 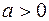
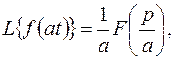 (3.6)
(3.6)
т.е. умножение аргумента оригинала на положительное число 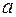 приводит к делению аргумента изображения и самого изображения
приводит к делению аргумента изображения и самого изображения  на это число.
на это число.
Доказательство.Найдем изображение функции 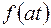 , т.е.
, т.е.
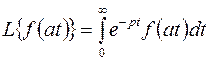 .
.
Сделаем замену переменной 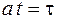 , откуда найдем
, откуда найдем 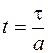 ,
, 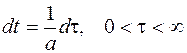 .
.
Тогда
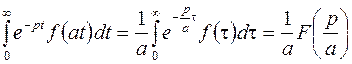 .
.
Таким образом,
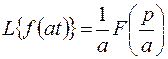 .
.
Проиллюстрируем применение этой теоремы на примере. Найти изображение функции 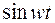 . Допустим, что нам известно соответствие (3.2) только для частного случая, когда
. Допустим, что нам известно соответствие (3.2) только для частного случая, когда 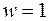 , т.е.
, т.е.
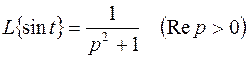 .
.
Применив теорему подобия к этому соответствию, найдем
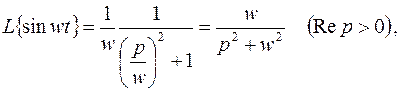
Что, естественно, совпадает с полученным ранее результатом.
3.1.4. Теорема смещения. Если 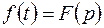 , то для любого числа
, то для любого числа 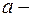 действительного или комплексного
действительного или комплексного 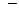 имеет место соотношение
имеет место соотношение
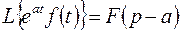 при
при 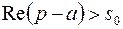 , (3.7)
, (3.7)
т.е. умножение оригинала на функцию 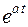 влечет за собой «смещение» аргумента изображения на
влечет за собой «смещение» аргумента изображения на 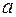 .
.
Доказательство.Если функция  является оригиналом, то при любом
является оригиналом, то при любом 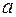 функция
функция 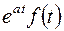 также является оригиналом, так как из оценки
также является оригиналом, так как из оценки 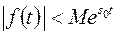 вытекает оценка
вытекает оценка
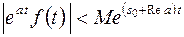 при
при  .
.
Значит показателем роста функции 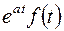 является число
является число 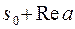 , а ее изображение определено в полуплоскости
, а ее изображение определено в полуплоскости 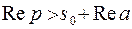 , иначе, для тех значений
, иначе, для тех значений 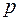 , для которых
, для которых 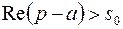 . Найдем изображение этой функции:
. Найдем изображение этой функции:
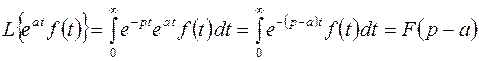 .
.
Легко заключить, что справедливо также соотношение
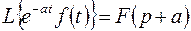 , если
, если 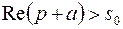 . (3.7 а)
. (3.7 а)
Теорема смещения дает возможность расширить таблицу соответствий: по известным операционным соотношениям находить изображения тех же функций, умноженных на экспоненту 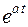 или
или 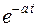 .
.
На основании теоремы (3.7) и полученных ранее соответствий (3.2), (3.3), найдем
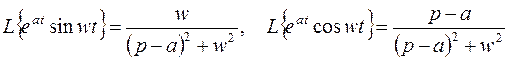 . (3.8)
. (3.8)
Используя (3.7а) и те же соответствия (3.2), (3.3), найдем изображения затухающих колебаний:
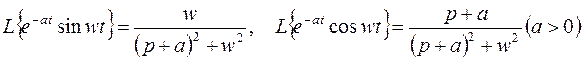 . (3.9)
. (3.9)
Аналогично из (3.4) и (3.5) получаем
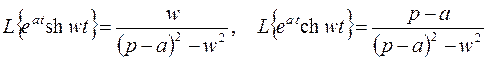 , (3.10)
, (3.10)
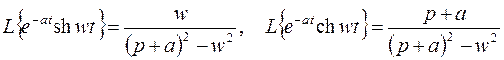 . (3.11)
. (3.11)
Область комплексной плоскости, в которой имеет место каждое из этих соответствий, оговорена в теореме смещения.
Пример 3.1. Найти изображение функций 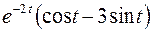 .
.
Решение. Используя свойство линейности и формулы  соответствия (3.9), получим
соответствия (3.9), получим
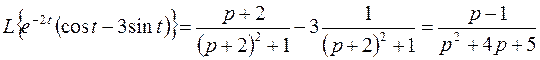 .
.
