Вероятностно-зональный критерий
Этот критерий является модификацией (и обобщением) предыдущего. В случае использования критерия максимальной ошибки считается, что все значения разностного сигнала (текущей ошибки) e = f – g лежат в диапазоне [–emax, emax], то есть распределение вероятностей для ε имеет, например, вид, показанный на рисунке 4.1.
Однако на практике во многих случаях это не выполняется. Простейшим примером является ситуация, когда изображение искажено аддитивным гауссовым шумом g = f + v, имеющим плотность распределения, которая нигде не обращается в нуль (см. рисунок 4.2):
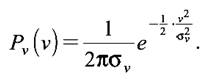
Разность e = f – g – имеет такое же распределение. Здесь можно оценить максимальную ошибку только с некоторой доверительной вероятностью p. Вероятностно-зональный критерий определяется парой чисел (emax, p).
Смысл этого критерия выражается формулой
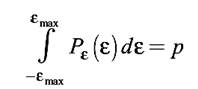
и иллюстрируется на рисунке 4.3.
Здесь, как и в предыдущем случае, часто возникают сложности при теоретической оценке. Значение такого показателя качества получают экспериментально, в результате анализа гистограммы распределения ошибки ε.
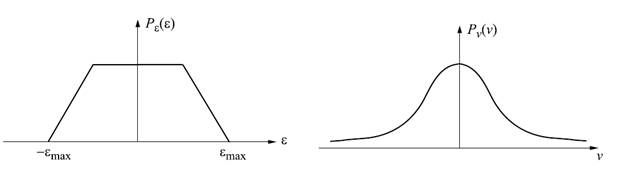
Рисунок 4.1 – Пример распределения вероятностей разностного сигнала
Рисунок 4.2 – Плотность распределения гауссова шума
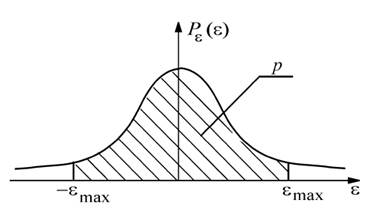
Рисунок 4.3 – Вероятностно-зональный критерий
ЛЕКЦИЯ 5. Точечные методы фильтрации изображений
Просветление.
Часто изображения бывают переэкспонированы или, наоборот, слишком затемнены. Для устранения данного эффекта выполняется операция просветления. К значению яркости каждого пикселя прибавляется некоторая величина, чаще всего определяемая по критерию визуального восприятия. В случае переэкспонирования данная величина отрицательная, при чрезмерном затемнении – положительная. При выполнении операции просветления необходимо осуществлять контроль за граничными значениями яркости, чтобы не уйти за верхний предел яркости пикселя или не получить отрицательные значения яркости.
Пороговая обработка.
Многие задачи обработки изображений связаны с преобразованием полутонового изображения в бинарное (двухградационное) или, по-другому, в графический препарат. Такое преобразование осуществляется для того, чтобы сократить информационную избыточность изображения, оставив в нем только ту информацию, которая нужна для решения конкретной задачи (например, очертания объектов), и исключив несущественные особенности (фон).
В ряде случаев требуемый графический препарат удается получить в результате пороговой обработки полутонового изображения. Она заключается в разделении всех отсчетов изображения на два класса по признаку яркости: объект и фон. Например, выполняется поэлементное преобразование вида
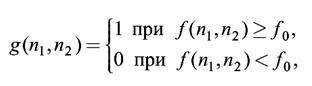
где f0 – некоторое «пороговое» значение яркости (рисунок 5.1). Основной проблемой здесь является выбор порога. Пусть исходное полутоновое изображение содержит интересующие нас объекты одной яркости на фоне другой яркости (типичные примеры: машинописный текст, чертежи, медицинские пробы под микроскопом и т.д.). Тогда плотность распределения вероятностей яркости должна выглядеть как два узких пика (в идеале два дельта-импульса); то есть так, как показано на рисунке 5.2а. В таком случае задача установления порога тривиальна: в качестве f0 можно взять любое значение между «пиками». На практике, однако, имеет место более сложный случай: изображение зашумлено, кроме того, как для объектов, так и для фона характерен некоторый разброс яркостей. В результате функция плотности распределения вероятностей размывается (рис. 5.2б).
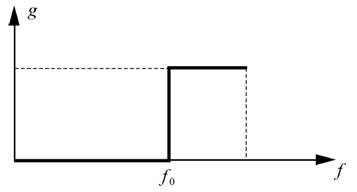
Рисунок 5.1 – Пример порогового преобразования яркости изображения
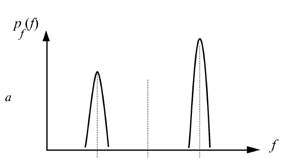
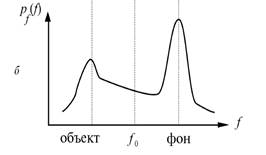
Рисунок 5.2 – Выбор порога при пороговой обработке
Часто бимодальность распределения тем не менее сохраняется. В такой ситуации можно выбрать порог f0, соответствующий положению минимума между максимумами (модами). В общем случае гистограммы распределения вероятностей яркостей, измеренные по реальным изображениям, могут оказаться унимодальными или, наоборот, иметь «изрезанный», полимодальный характер (рисунок 5.3).
Укажем некоторые методики определения порога в этих ситуациях. Методика 1 заключается в аппроксимации участка гистограммы между пиками какой-либо гладкой функцией, например, параболой, и нахождении ее минимума через производную (рисунок 5.3а). По существу такая аппроксимация реализует сглаживание гистограммы. Для этого сглаживания можно построить специальный фильтр низких частот.
Методика 2 основана на том, что иногда удается подобрать хорошие модели отдельно для плотностей распределения вероятностей яркости объекта и фона. Тогда можно произвести аппроксимацию гистограммы суммой этих плотностей вероятностей (рис. 5.3б):
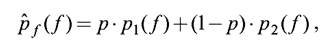
где p1(f), p2(f) – аналитически заданные функции плотности вероятностей для объекта и фона, p — вероятность объекта (точнее, доля площади изображения, занимаемая объектом). Эта вероятность и параметры указанных плотностей распределения вероятностей яркости, как правило, подлежат оценке.
После оценки параметров можно выбрать порог f0 в соответствии с принципом максимального правдоподобия, то есть из соотношения
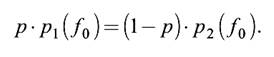
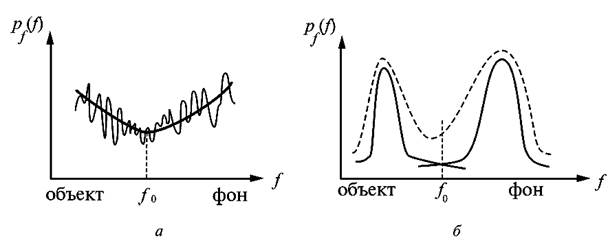
Рисунок 5.3 – Методики определения порога при пороговой обработке
Отметим, что данный способ определения порога сохраняет работоспособность и тогда, когда бимодальность гистограммы скрыта из-за большого разброса яркостей и малой вероятности p. Основным недостатком метода является сложность аппроксимации.
