Полосовой фильтр как последовательное соединение фильтров высоких и низких частот

При последовательном соединении фильтров высоких и низких частот их передаточные функции перемножаются. В результате получаем передаточную функцию полосового фильтра. Это наиболее простой способ получения полосового фильтра, но при этом повышается размерность.

Тангенциальный фильтр

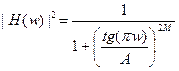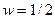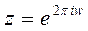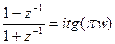Для случай фильтра низких частот в синусоидальном фильтре на конце интервала не достигался 0. Рассмотрим функцию . Теперь получается передаточная функция с нулем при . Если , то . Используя тот же прием, получим, что 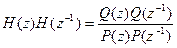. Для отыскания коэффициентов многочленов в числителе и знаменателе рассматривают нули и полюса передаточной функции.

ЛЕКЦИЯ 22. FIR фильтры

Полосовой фильтр на основе фильтра низких частот

В предыдущей лекции было показано, каким образом можно построить различные фильтры. Оказывается, любой из таких фильтров можно получить на основе фильтра низких частот с помощью универсальной процедуры.

Пусть имеется сигнал 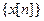с преобразованием Фурье 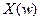. Рассмотрим новую последовательность 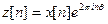. По определению 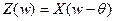. Если нам нужен полосовой фильтр, можем поступить следующим образом. Сдвиг осуществляется генератором на основе осциллятора, о котором будет сказано ниже. Обратный сдвиг осуществляется так же.

Сдвиг

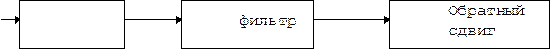Непосредственное применение указанного способа не удобно, поскольку приходится работать с комплексными числами, и в результате обратного сдвига получается, как правило, комплексный сигнал. Выход заключается в преобразовании 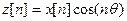. В результате 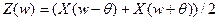. Если исходный сигнал имеет ограниченный спектр и 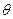выбран так, что носител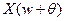и и 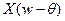не пресекаются, задача решается без применения комплексных чисел. Например, пусть спектр 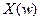находится в интервале 2kHz-4kHz, и требуется получить лишь часть сигнала в диапазоне 2.5kHz-3.5kHz. Выбираем 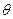=3kHz и используем фильтр низких частот с полосой пропускания 0.5kHz. После обратного сдвига придется использовать еще один фильтр низких частот с полосой пропускания 3.5kHz.

Фильтр как осциллятор

Выше отмечалось, что для сдвига спектра последовательности требуется источник, генерирующий последовательности вида 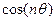. Обычный способ генерирования таких последовательностей не годится, поскольку возникает проблема подсчета фукнции от большого аргумента. Существует альтернативный способ генерации, основанный на теории фильтров.

Для устойчивости фильтра достаточно, чтобы все корни находились внутри единичной окружности. Если корни лежат на окружности, фильтр можно использовать для генерации. Рассмотрим уравнение

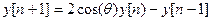(1)

Уравнение 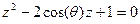имеет два корня 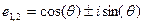, поэтому (1) можно записать в виде 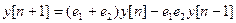. Из полученного равенства следуют два рекуррентных соотношения: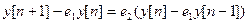 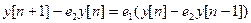. Вычитая из первого уравнения второе, получим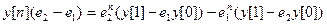

Полагая , получим 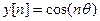. Аналогично, взяв 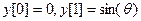, найдем, что .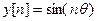