Используя свойство линейности и соответствия (10), (9) из таблицы оригиналов и их изображений, найдем

б) заметим, что  Согласно свойству линейности и соответствиям (1), (2) из таблицы получим, что
Согласно свойству линейности и соответствиям (1), (2) из таблицы получим, что  . Тогда для заданного изображения
. Тогда для заданного изображения  оригинал может быть найден с помощью теоремы запаздывания. Полагая в (3.12)
оригинал может быть найден с помощью теоремы запаздывания. Полагая в (3.12)  , получим
, получим
 .
.
Если изображение  представляем собой правильную рациональную дробь
представляем собой правильную рациональную дробь  , где
, где  и
и  многочлены от
многочлены от 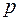 , причем степень числителя меньше степени знаменателя, то при нахождении оригинала поступают следующим образом: разлагают дробь на сумму простейших дробей вида
, причем степень числителя меньше степени знаменателя, то при нахождении оригинала поступают следующим образом: разлагают дробь на сумму простейших дробей вида

Находят оригинал для каждого слагаемого и, суммируя, получают оригинал данной функции.
Пример 4.3. Найти оригинал  для изображения
для изображения

Решение. Представим правильную рациональную дробь  в виде суммы простейших дробей
в виде суммы простейших дробей

Чтобы найти коэффициенты  приведем дроби к общему знаменателю, в результате чего будем иметь
приведем дроби к общему знаменателю, в результате чего будем иметь

Полагая  , найдем, что
, найдем, что  . Приравнивая коэффициенты при одинаковых степенях
. Приравнивая коэффициенты при одинаковых степенях 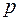 , получим систему уравнений
, получим систему уравнений


откуда найдем  Следовательно,
Следовательно,
 .
.
На основании свойства линейности и соответствий (2), (4), (6), (5) из таблицы получаем
 .
.
Рассмотренный прием отыскания оригинала путем разложения дробно-рациональной функции  на сумму простейших дробей хорош своей общностью, однако часто приводит к громоздким выкладкам при определении коэффициентов. В таких случаях более прост переход от изображения к оригиналу при помощи теоремы разложения, которая носит название второй теоремы разложения Хевисайда.
на сумму простейших дробей хорош своей общностью, однако часто приводит к громоздким выкладкам при определении коэффициентов. В таких случаях более прост переход от изображения к оригиналу при помощи теоремы разложения, которая носит название второй теоремы разложения Хевисайда.
Теорема разложения.
Пусть изображение представляет правильную рациональную дробь*)[41]
 *) (4.3)
*) (4.3)
При разложении  на простейшие дроби могут иметь место два случая: I. Корни знаменателя
на простейшие дроби могут иметь место два случая: I. Корни знаменателя  простые; II. Корни знаменателя кратные. Рассмотрим оба случая.
простые; II. Корни знаменателя кратные. Рассмотрим оба случая.
I. Знаменатель дроби (4.3) имеет только простые корни. Обозначим 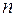 простых корней знаменателя
простых корней знаменателя  через
через  . Тогда имеет место разложение
. Тогда имеет место разложение

и  можно представить в виде суммы простейших дробей
можно представить в виде суммы простейших дробей
 (4.4)
(4.4)
Найдем коэффициенты  . Для определения
. Для определения 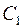 умножим почленно это равенство на
умножим почленно это равенство на  и затем перейдем к пределу при
и затем перейдем к пределу при  .
.

При  второе слагаемое в правой части равенства стремится к нулю, а его левая часть становится неопределенностью вида
второе слагаемое в правой части равенства стремится к нулю, а его левая часть становится неопределенностью вида  . Тогда
. Тогда

Аналогично определяется любой коэффициент  .
.
 откуда
откуда
 .
.
Подставляя  в равенство (4.4), получаем
в равенство (4.4), получаем

Воспользовавшись свойством линейности и соотношением  ,
,
Получим формулу для искомого оригинала
 (4.5)
(4.5)
Формула (4.5) представляет собой общую формулу теоремы разложения для случая простых корней знаменателя изображения.
Частный случай. В частном случае, когда один из корней знаменателя  равен нулю, формуле (4.5) можно придать несколько другой вид. Пусть
равен нулю, формуле (4.5) можно придать несколько другой вид. Пусть
 . (4.6)
. (4.6)
Обозначим корень, равный 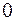 , через
, через  . Тогда корни
. Тогда корни  определяются из уравнения
определяются из уравнения  . Продифференцируем равенство (4.6) по
. Продифференцируем равенство (4.6) по 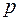 и найдем
и найдем 

