Задания и указания к их выполнению

МАТРИЧНЫЙ МЕТОД РАСЧЕТА ОПТИЧЕСКОЙ СИСТЕМЫ

Цель работы: ознакомление с матричным методом построения изображений в оптических системах, расчет характеристик элементов оптических систем.

Общие сведения

Траектория меридиональных лучей в оптической системе состоит из отрезков прямых линий между плоскими и сферическими границами раздела различных однородных сред. При этом в любой плоскости, перпендикулярной оптической оси (называемой в дальнейшем опорная плоскость ОП), луч можно полностью определить двумя параметрами: координатой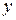точки его пересечения с опорной плоскостью и углом 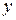, который луч составляет с оптической осью системы. 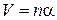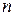В принятом в настоящее время методе расчета направление распространения характеризуется произведением , где - показатель преломления среды, в которой распространяется луч. При расчетах используется общее в геометрической оптике правило знаков.

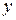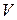Для параксиальной области преобразование параметров и при переходе от одной опорной плоскости к другой будет линейным:

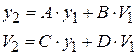.(3.1)

Это преобразование можно записать в матричном виде:

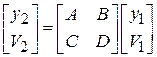. (3.2)

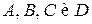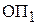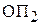Элементы матрицы зависят от того, какие преломляющие поверхности и какие среды находятся между и . Прохождение луча через оптическую систему может быть описано путем перемножения матриц соответствующих элементов. При этом достаточно использовать матрицы преобразования для трех основных элементов: участка однородной среды, преломляющей и отражающей поверхностей. Если заданы параметры луча в плоскост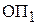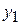и (и 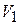), то параметры луча на выходе плоскости 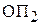могут быть вычислены по формуле (3.2).

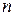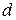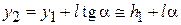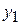Для участка однородной среды с показателем преломления и толщиной можно записать , где и 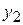высота луча в начале и конце участка соответственно, 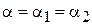– угол под которым распространяется луч (рис. 3.1). В матричной форме

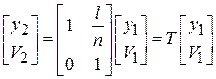. (3.3)

Матрица 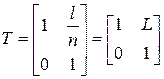, входящая в выражение (3.3)называется передаточной матрицей; 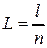– приведенная толщина оптического промежутка.

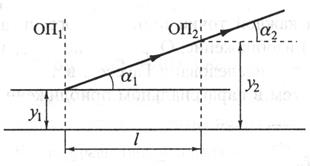
Рис. 3.1. Прохождение луча через участок однородной среды

Для сферической преломляющей поверхности с радиусом кривизны 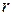разграничивающей среды с показателями преломления 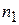и 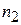в параксиальной области действительно уравнение нулевого луча 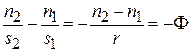, где 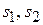– расстояния от вершины преломляющей поверхности до предметной точки на оптической оси и её изображения соответственно, 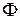– оптическая сила преломляющей поверхности (рис. 3.2). Учитывая, что 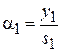, 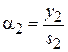и 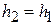уравнение нулевого луча также можно переписать в виде 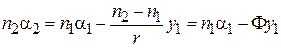. В матричной форме:

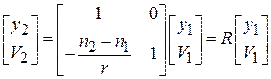. (3.4)

Матрица 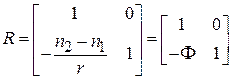называется преломляющей матрицей поверхности.

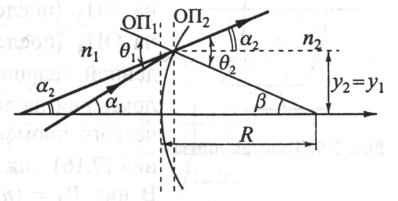
Рис. 3.2.Преломление луча на сферической границе раздела

Отражение света от сферической поверхности можно условно рассматривать как преломление в среду с отрицательным показателем преломления 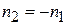. Следовательно, матрица, описывающая отражение от сферической поверхности, имеет точно такой же вид, как и преломляющая матрица поверхности, если 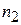заменить на 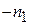, а именно 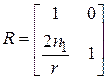. При расчете систем содержащих зеркала следует учитывать, что на участках где свет распространяется в направлении противоположном от первоначального (справа налево) показатели преломления и расстояния берутся с противоположным знаком, а знак радиусов кривизны не изменяется

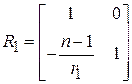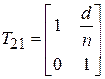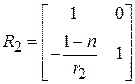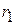Рассмотрим в качестве примера линзу – простейшую оптическую систему. Матрица линзы может быть получена перемножением трех матриц составляющих её элементов – преломляющей матрицы передней сферической поверхности , передаточной матрицы и преломляющей матрицы задней сферической поверхности где и 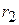- радиусы кривизны передней и задней поверхностей линзы, 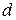– толщина линзы, 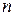– показатель преломления материала линзы. Результирующая матрица для толстой линзы имеет вид

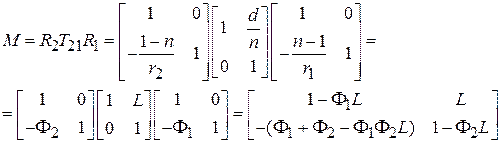. (3.5)

В случае тонкой линзы толщина линзы 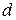считается пренебрежимо малой и выражение (3.5) существенно упрощается:

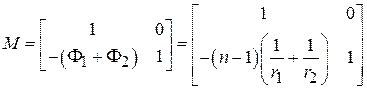. (3.6)

Отражение пучка от сферического зеркала можно условно представить как преломление в среду с отрицательным показателем преломления 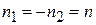. При этом матрица сферического зеркала принимает вид:

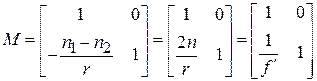. (3.7)

Матрица сложной оптической системы состоящей из 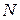элементов вычисляется как произведение матриц соответствующих элементов и передаточных матриц для воздушных промежутков между ними:

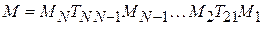. (3.8)

Пусть известны координаты луча в произвольной плоскости в пространстве предметов 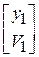, отстоящей от первой преломляющей поверхности оптической системы 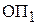на расстояние 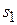. Найдем координаты луча в произвольной плоскости в пространстве изображений 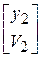, отстоящей от последней преломляющей поверхности оптической системы 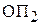на расстояние 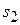, т.е. сделаем преобразование от плоскости предмета к плоскости изображения. Для этого необходимо перемножить три матрицы: передаточную матрицу от плоскости предмета до первой преломляющей поверхности оптической системы 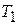, матрицу оптической системы 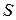и передаточную матрицу от последней преломляющей поверхности оптической системы до плоскости изображения :

,

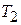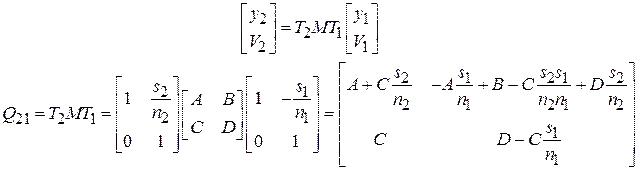где 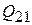– матрица преобразования от предмета к изображению.

Под изображением в идеальной оптической системе подразумевается такое отображение плоскости предмета, когда все лучи исходящие от точки предмета сходятся в одной точке плоскости изображения и все точки отображаются с одинаковым увеличением. Из формулы следует, что линейное увеличение 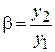зависит от угла наклона луча 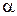, следовательно, при произвольном 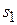и 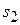четкого изображения не формируется. Чтобы это условие выполнялось, необходимо обнулить верхний элемент второго столбца матрицы 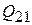: 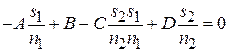. Полученное выражение позволяет при известном положении предметной плоскости 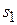найти положение сопряженной ей плоскости изображения 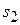. С учетом данного условия матрица 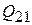приобретает вид

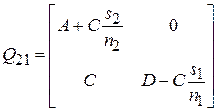. (3.9)

Из выражения (3.7) следует, что линейное увеличение равно 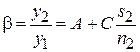. Нетрудно доказать, что определители матриц всех элементов оптической системы равны единице, откуда следует, что определитель матрицы 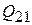также равен единице 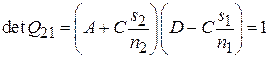, и её можно записать в виде .

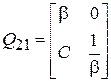Пара сопряженных плоскостей, для которых линейное увеличение в параксиальной области положительно и равно единице 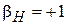называются передней 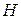и задней 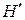главными плоскостями. Их пересечения с оптической осью – передняя и задняя главные точки.

Положение передней 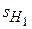и задней 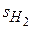главных плоскостей определяется из матрицы 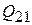для главных плоскостей:

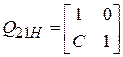
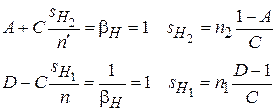. (3.10)

Главных плоскости и главные точки обладают двумя важными свойствами, которые широко используются при построении изображений:

– Если произвольный луч пересекает переднюю главную плоскость на некоторой высоте, то после прохождения через оптическую систему он пересекает заднюю главную плоскость на той же самой высоте.

– Если первая и последняя среды одинаковы 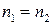, то всякий луч, входящий в оптическую систему через переднюю главную точку под некоторым углом, по выходе из системы пройдет через заднюю главную точку под тем же углом.

Пусть предметная точка находится на оптической оси слева в бесконечности, т.е в систему входит параллельный пучок лучей. Ее изображение будет в точке 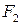, которая называется задним фокусом оптической системы. Плоскость, проведенная через задний фокус перпендикулярно оптической оси – задняя фокальная плоскость. Этому положению соответствует увеличение равное нулю 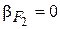. Положение заднего фокуса может быть найдено из матрицы преобразования от предмета к изображению:

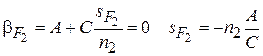. (3.11)

Теперь пусть предметная точка находится на оптической оси слева в точке 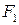так, что ее изображение удалено в бесконечность, т.е. из системы выходит параллельный пучок лучей. Точка 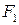называется передним фокусом; плоскость, проведенная через передний фокус перпендикулярно оптической оси – передняя фокальная плоскость. Этому положению соответствует увеличение равное бесконечности 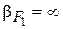. Положение переднего фокуса также может быть найдено из матрицы преобразования от предмета к изображению:

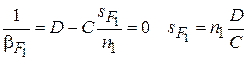. (3.3)

Расстояния от главных точек до соответствующих фокусов называются передним 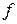и задним 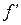фокусными расстояниями

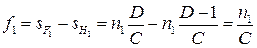
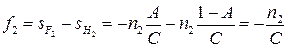. (3.13)

Возьмем отношение 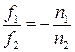. Так как 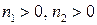, фокусные расстояния системы имеют разные знаки; если 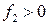система считается положительной (передний фокус левее передней главной плоскости, задний фокус правее задней главной плоскости), 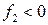– отрицательной ой (передний фокус правее передней главной плоскости, задний фокус левее задней главной плоскости). Если первая и последняя среды одинаковы, то .

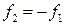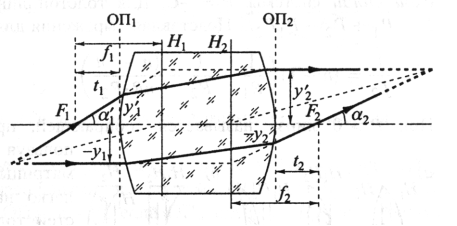
Рис. 3.3. Кардинальные элементы оптической системы

Фокусы и главные плоскости являются кардинальными элементами оптической системы (рис. 3.3). Их положение полностью определяется элементами матрицы оптической системы (таблица 3.1). Используя элементы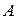и 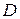, можно найти положение главных плоскостей оптической системы; фокусное расстояние оптической системы определяется элементом 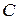матрицы преобразования лучей: при 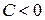– оптическая система положительна (собирающая линза), при 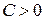– отрицательна (рассеивающая линза).

Таблица 3.1

Расстояние	Элементы матрицы при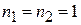

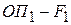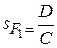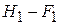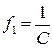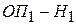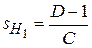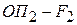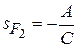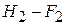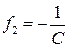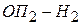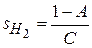При известном положении кардинальных элементов матрица преобразования от предмета к изображению может быть записана в виде:

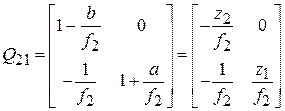, (3.14)

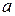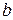где и – расстояния от передней главной плоскости до предмета и от задней главной плоскости до изображения; 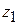и 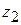– расстояния от передней фокальной плоскости до предмета и от задней фокальной плоскости до изображения.

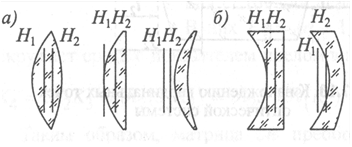
Рис. 3.4. Расположение главных плоскостей для толстых линз

Элементы матрицы 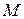позволяют определить положение кардинальных элементов оптической системы – главных и фокальных плоскостей. После этого любая сколь угодно сложная оптическая система может быть заменена эквивалентной линзой, положение главных и фокальных плоскостей которой совпадает с положением главных и фокальных плоскостей исследуемой системы. В дальнейшем при определении параметров лучей после прохождения оптической системы и построении изображений достаточно рассмотреть соответствующую эквивалентную линзу.

Матрица оптической системы может быть использована для преобразования параметров не только отдельных лучей, но и параксиальных пучков в целом. Рассмотрим гомоцентрический параксиальный пучок, точка схода которого расположена на оптической оси. На любой опорной плоскости его можно охарактеризовать приведенным радиусом кривизны волнового фронта 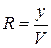. Значение радиуса кривизны изменятся при преломлении на сферической границе раздела и при прохождении участка однородной среды. Пусть на опорной плоскости 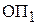пучок характеризуется радиусом кривизны 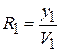. Тогда на опорной плоскости :

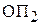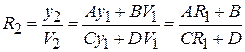. (3.15)

Соотношение (3.13), называемое правилом ABCD, позволяет вычислить приведенный радиус кривизны волнового фронта с центром на оптической оси при переходе от одной опорной плоскости к другой.

Правило ABCD применимо не только для гомоцентрических, но также и для гауссовых пучков. Гауссов пучок характеризуется двумя параметрами: радиусом кривизны волнового фронта 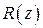и радиусом поперечного сечения 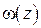. Поэтому вводят их комбинацию 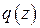называемую комплексным радиусом кривизны, таким образом, что

.

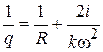При прохождении гауссова пучка через произвольную центрированную оптическую систему изменение комплексного радиуса кривизны можно находить с помощью того же правила ABCD, что и для вещественного :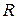

.

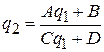Задания и указания к их выполнению

Лабораторная работа выполняется на компьютере в специальной программе, составленной в форме диалога. При выполнении расчетов в программу должны быть последовательно введены характеристики всех элементов рассматриваемой оптической системы, каждому из которых сопоставляется матрица одного из трех типов: матрица свободного пространства, матрица тонкой линзы или матрица толстой линзы. Также должны быть указаны показатели преломления сред на входе (до опорной плоскости 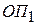) и выходе (после опорной плоскости 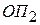). Поэтому первой и последней должны быть введены матрицы свободного пространства с 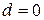и 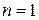, т.е. для воздуха.

Программа позволяет рассчитать элементы матрицы оптической системы, положение кардинальных элементов, а также координаты луча и кривизну волнового фронта на выходе из оптической системы по известным координатам луча на входе. Результаты расчета могут быть сохранены в html файл.

Задание 1. Определить положение главных плоскостей для следующих одиночных линз:

– двояковыпуклой: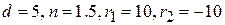

.

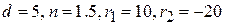– плосковыпуклой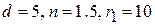

.

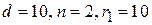– выпукловогнутой: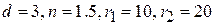

.

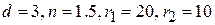– двояковогнутой: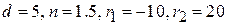

.

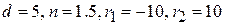– плосковогнутой: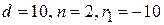

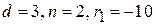
Для линз всех типов параметры луча на входе , .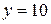

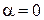Задание 2.Рассчитать характеристики заданной оптической системы, определить положение кардинальных элементов (главных плоскостей и фокусов) и вычислить параметры луча после прохождения оптической системы по известным параметрам на входе. Определить положение изображения по заданному положению предмета.

Тип оптической системы задается преподавателем для каждой бригады.

Содержание отчета

Отчет по работе должен содержать:

1. Описание матричного метода расчета оптических систем.

2. Итоговые таблицы результатов расчетов.

3. Оптические схемы положения главных плоскостей для толстых линз.

3.4 Контрольные вопросы

1. Что собой представляют кардинальные элементы оптической системы? Как отсчитываются фокусные расстояния?

2. Какой вид имеют матрицы участка однородной среды, сферической границы раздела, тонкой и толстой линзы?

3. Укажите особенности применения матричного метода при расчете систем содержащих зеркала.

4. Каким образом можно найти матрицу оптической системы?

5. Как из матрицы оптической системы определить положение кардинальных элементов?

6. Как расположены главные плоскости в различных толстых линзах?

Список рекомендуемой литературы

Бутиков Е. И. Оптика. СПб.: BHV., 2003.

Матвеев А. Н. Оптика. М.: Высш. шк., 1985.

Евтихиев Н. Н. Информационная оптика. М.: Изд-во МЭИ, 2000.