Упражнения для самостоятельной работы. 78. Вычислить интеграл , если

78. Вычислить интеграл 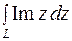, если

а) 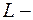отрезок действительной оси от точки 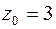до ;

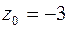б) 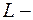полуокружность , .

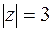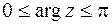79. Вычислить 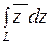, если

а) 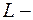отрезок прямой, соединяющий точк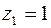и и ;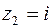

б) 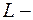дуга окружности 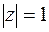от точки 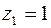до точки ;

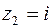в) 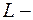замкнутый контур: , .

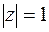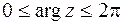80. Вычислить интеграл .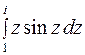

81. Вычислить 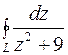, если

а) точки 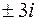вне контура ;

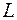б) точка 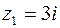лежит внутри, а 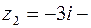вне контура ;

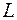в) точка 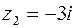лежит внутри, а 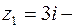вне контура;

г) точки 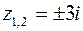лежат внутри контура .

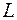82. Вычислить интеграл 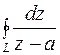, где 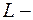окружность с центром в точке 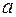и радиусом .

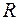83. Вычислить .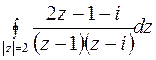

84. Вычислить:

а) ;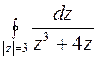

б) ;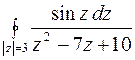

в) ;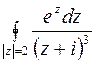

г) ;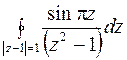

д) .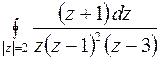

РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ

Ряды с комплексными членами

Ряд

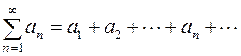, (6.1)

где 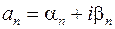, есть числовой ряд с комплексными членами.

Если сходится ряд 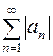, то сходится и ряд (6.1), называемый в этом случае абсолютно сходящимся.

Сходимость ряда (6.1) с комплексными членами эквивалентна сходимости рядов 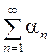и 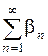с действительными членами. В силу этого ряд теорем, относящихся к рядам с действительными членами, в том числе признаки сходимости, переносятся на ряды с комплексными членами.

Функциональный ряд вида

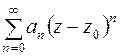, (6.2)

где 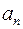, 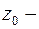комплексные числа, 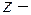комплексное переменное, называется степенным рядомпо степеням 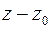. В частности, при 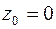имеем ряд 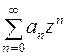по степеням .

Как следует из теоремы Абеля, областью степенного ряда (6.2) является круг 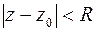с центром в точке , радиус 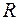которого может быть определен применением признаков Даламбера и Коши. Приведем их формулировки.

Признак Даламбера.Если существует конечный предел 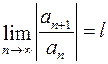, то при 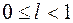ряд (6.1) сходится абсолютно, а при расходится (при 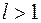расходится не только ряд 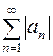, но и ряд (6.1)).

Признак Коши.Для числового ряда (6.1) положим 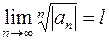. Тогда, если 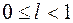, то ряд сходится абсолютно, если ряд расходится.

Обобщением степенного ряда (6.2) является ряд по целым отрицательным степеням 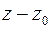вида

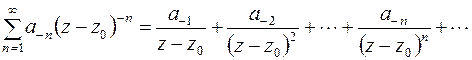(6.3)

Областью сходимости этого ряда является внешность круга 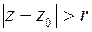, где 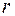определяется также с помощью признаков Даламбера и Коши.

Ряды Тейлора и Лорана

Функция 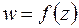, однозначная и аналитическая в точке , разлагается в окрестности этой точки в степенной ряд

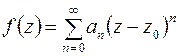, (6.4)

коэффициенты которого определяются по формулам

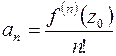или 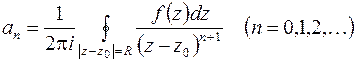. (6.5)

Этот ряд называется рядом Тейлора для функции .

Радиус 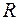круга сходимости 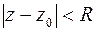ряда Тейлора (6.4) - (6.5) равен расстоянию от точки до ближайшей к особой точки функции (особая точка – это такая точка, в которой функция не является аналитической).

Приведем разложения в ряды Тейлора некоторых элементарных функции в окрестности точки .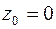

,

, ,

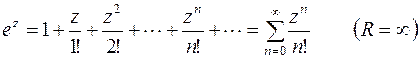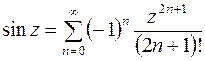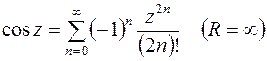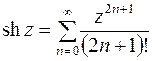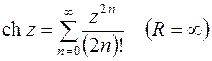, , (6.6)

, .

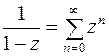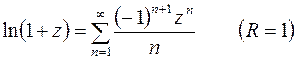Функция , однозначная и аналитическая в кольце 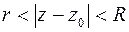(не исключаются случаи, когда 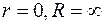), разлагается в этом кольце в обобщенный степенной ряд

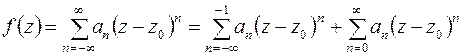, (6.7)

коэффициенты которого определяются по формулам

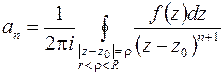. (6.8)

Этот ряд называется рядом Лоранафункции .

В формуле (6.7) 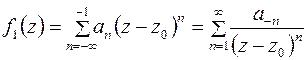называется главной частью ряда Лорана, а ряд 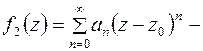называется правильной частью ряда Лорана.

Формула (6.8) малоудобна для вычисления коэффициентов ряда Лорана, поэтому часто для разложения функции в ряд Лоран пользуются искусственными приемами, которые будут рассмотрены на примерах. Ряды Тейлора и Лорана функции 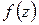определяются единственным образом. Эти ряды в области сходимости можно почленно дифференцировать и интегрировать.

УПРАЖНЕНИЯ

85. Исследовать на сходимость ряд .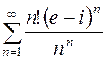

Решение. К ряду из абсолютных величин членов данного ряда применим признак Даламбера:

.

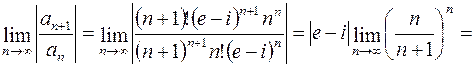
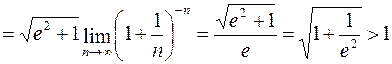Следовательно, ряд расходится.

86. Найти радиус и круг сходимости рядов:

а) 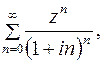б) .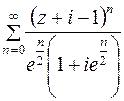

Решение. а) Применим признак Коши к ряду из абсолютных величин данного ряда

.

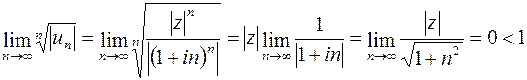Следовательно, данный ряд сходится абсолютно, для всех . Роль круга сходимости выполняется вся плоскость, радиус сходимости .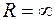

б) По признаку Даламбера имеем

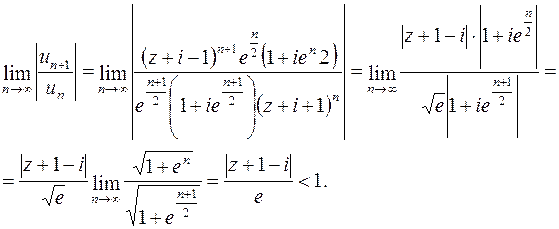
Отсюда заключаем, что ряд сходится абсолютно в области 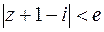, т.е. в круге радиуса 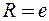с центром в точке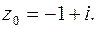

87. Найти область сходимости ряда .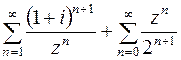

Решение. Рассмотрим отдельно ряды по положительным и отрицательным степеням . Ряд 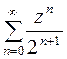можно рассматривать как ряд, составленный из членов геометрической прогрессии со знаменателем 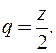Такой ряд сходится при условии 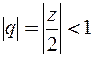, т.е. в круге 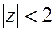радиуса 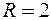. Для ряда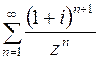

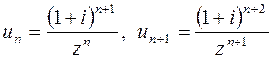, где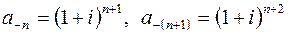

Применяя признак Даламбера, получаем

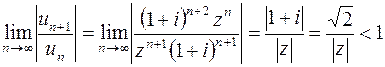, откуда 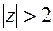, т.е.

областью сходимости ряда по отрицательным степеням 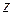является внешность круга радиуса с центром в точке .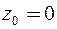

Таким образом, данный степенной ряд Лорана сходится в кольце .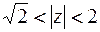

88. Разложить функцию 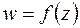в ряд Тейлора в окрестности точки и указать радиус сходимости:

а) ;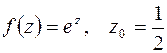

б) ;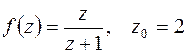

в) .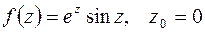

Решение. а) Воспользуемся известным разложением для 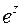(формулы (6.6)); с этой целью преобразуем функцию к виду 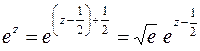. Заменяя в разложении на 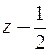, получим следующий ряд Тейлора 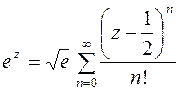, для которого радиус сходимости .

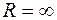б) Выделим в дроби целую часть, а затем знаменатель правильной дроби преобразуем так, чтобы в нем было слагаемое 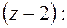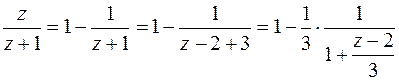. Используя разложение функции 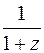(формулы (6.6) ), получим

.

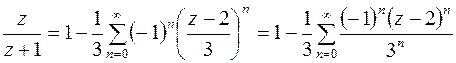Радиус сходимости 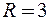. Так как ближайшая особая точка 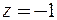удалена от центра круга сходимости 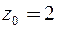на расстоянии, равном 3.

в) Представим данную функцию следующим образом:

.

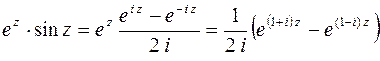Тогда

.

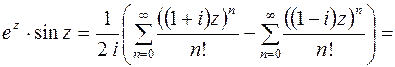
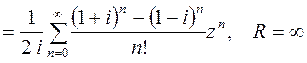89. Разложить в ряд Лорана функцию 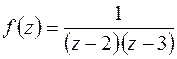по степеням (приняв ).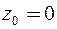

Решение.Функция не аналитична в точках 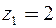и 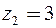. Следовательно, можно выделить три кольца с центром в точке 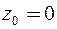, в каждом из которых является аналитической:

а) круг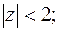

б) кольцо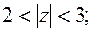

в) 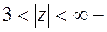внешность круга .

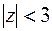Разложим функцию на сумму простейших дробей

.

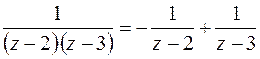а) В круге 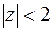функция аналитична. Коэффициенты ряда Лорана при степенях с отрицательными показателями равны нулю, ибо они выражаются интегралами от аналитической функции по замкнутому контуру. Ряд Лорана совпадает с рядами Тейлора. Запишем каждую из дробей в виде

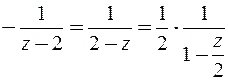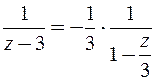; и воспользуемся разложением в ряд Тейлора функции 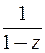(формулы (6.6)), в силу чего имеем

, ,

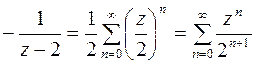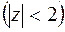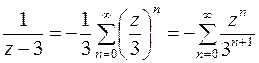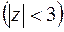, и

.

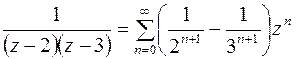Ряд Лорана содержит только правильную часть:

, .

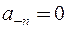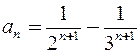
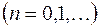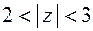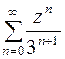б) В кольце ряд для функции 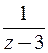сходится, поэтому по-прежнему 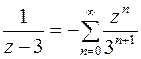, а ряд 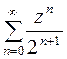для функции 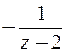расходится, поэтому функцию 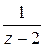преобразуем к виду 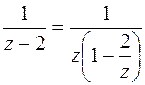. Представим 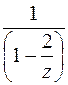в виде суммы геометрической прогрессии со знаменателем .

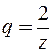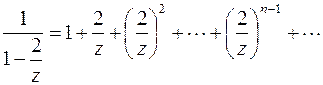. Этот ряд сходится для 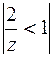, т.е. при 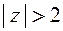. Тогда .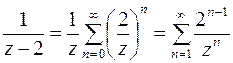

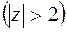Таким образом, 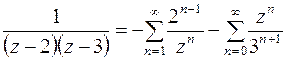. Ряд Лорана содержит правильную и главную части: , .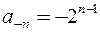

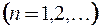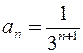
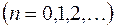в) В области 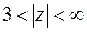ряд 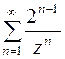для функции 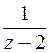сходится, а ряд 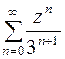для функции 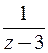расходится. Поэтому функцию 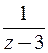представим в виде .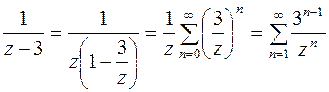

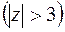Тогда имеем .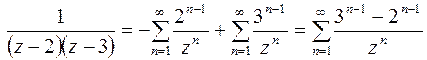

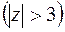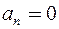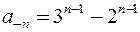
Ряд Лорана содержит только главную часть: , 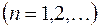. Приведенный пример показывает, что для одной и той же функции ряд Лорана имеет, вообще говоря, разный вид для разных областей.

90. Разложим в ряд Лорана в окрестности точки следующие функции:

а) , ;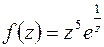

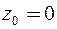б) , ;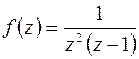

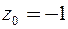в) , .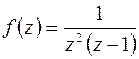

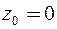Решение. а) Функция 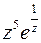аналитична всюду, кроме 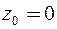. Поэтому ее можно разложить в ряд Лорана в кольце: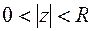 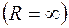. В силу (6.6) имеем .

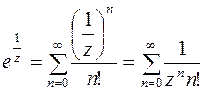Отсюда получим

.

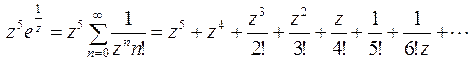б) Функция 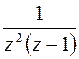аналитична в точке 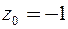. Поэтому в окрестности точки 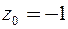ее можно разложить в ряд Тейлора, причем ряд будет сходиться в круге с центром 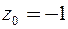радиуса 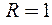(расстояние от точки 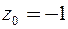до ближайшей точки 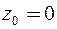). Разложим функцию на сумму простейших дробей: .

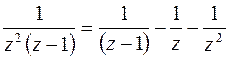В силу (6.6) имеем

,

.

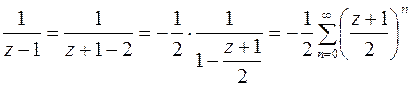
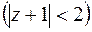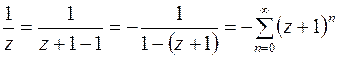
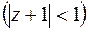Ряд для функции 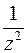найдем почленным дифференцированием ряда функции . .

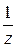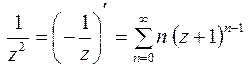
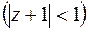Таким образом, в круге 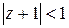получаем

.

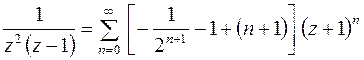в) Функция 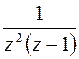аналитична в кольце 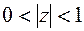, поэтому ее ряд Лорана имеет вид

.

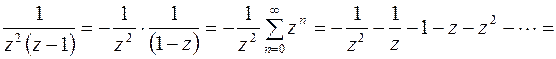
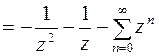Главная часть Лорана в окрестности 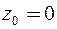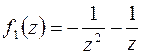, а правильная .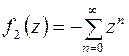