Низкочастотные фильтры
Низкочастотные пространственные фильтры оставляют низкочастотные компоненты изображения нетронутыми и ослабляют высокочастотные компоненты. Такие фильтры используются для понижения визуального шума, содержащегося в изображении, а также для удаления высокочастотных компонент из изображения с тем, чтобы можно было тщательнее исследовать содержание низкочастотных компонент. По мере того как уменьшается содержание высокочастотных компонент, могут быть идентифицированы более слабые изменения низкой частоты.
Частотная характеристика идеального НЧ фильтра имеет вид:
| |
| |
| |

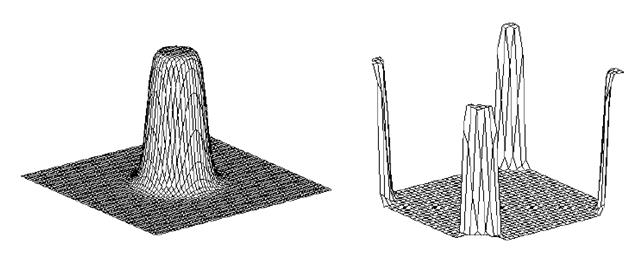
На рисунке 20.1 приведены графики частотной характеристики фильтра Баттерворта при r = 70 и k = 10.
а) б)
Рисунок 20.1 – График частотной характеристики фильтра Баттерворта при r = 70 и k = 10: а) – центрированная характеристика, б) нецентрированная
Частотная характеристика гауссовского НЧ фильтра имеет вид:
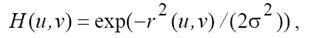
где у имеет смысл частоты среза (rср).
Частотная фильтрация выполняется по алгоритму:
− выполнить двумерное ДПФ входного изображения f(x,y) (подвергаемого фильтрации) размером (NxM), получить F(u,v);
− вычислить передаточную характеристику фильтра в частотной области, размер матрицы (NxM); выполнить децентрирование характеристики H(u,v);
− выполнить поточечное умножение
S(u,v) = F(u,v)H(u,v), "(u Î [0, N −1],v Î[0,M −1]);
− выполнить ОДПФ спектра S(u,v).
ЛЕКЦИЯ 21. Дискретное преобразование Фурье. Высокочастотный и полосовой фильтры
Высокочастотные фильтры выделяют высокочастотные компоненты изображения, оставляя содержание низкочастотных компонент нетронутым. Содержание низкочастотных компонент увеличивается по отношению к содержанию высокочастотных компонент. Такая фильтрация используется в тех случаях, когда необходимо исследовать объекты с высокой пространственной частотой. Области изображения с высокой частотой будут хорошо освещены (станут ярче), а части с низкой частотой станут черными. Иногда резкость изображения увеличивается после высокочастотной фильтрации за счет выделения шума изображения. При использовании высокочастотной фильтрации возможно усиление резкости краев, смазанных на экспериментальном изображении. На рисунке 21.1 представлено действие высокочастотного фильтра на изображение.
 |  |
| Исходное изображение. | Высокочастотная фильтрация |
Рисунок 21.1 – Применение высокочастотной фильтрации.
Фильтр высоких частот
Рассмотрим функцию 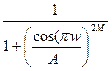 . Это передаточная функция фильтра высоких частот. С другой стороны, из выражения
. Это передаточная функция фильтра высоких частот. С другой стороны, из выражения 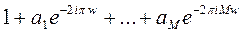 при указанной замене получим
при указанной замене получим 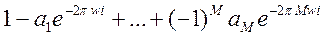 . Это означает, что фильтр высоких частот можно получить из фильтра низких частот заменой знака у коэффициентов с нечетными индексами.
. Это означает, что фильтр высоких частот можно получить из фильтра низких частот заменой знака у коэффициентов с нечетными индексами.
Полосовой фильтр
Рассмотрим выражение 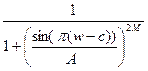 , где
, где 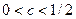 . Очевидно, что эта функция достигает своего максимума при
. Очевидно, что эта функция достигает своего максимума при 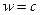 . Это означает, что передаточная функция изображает полосовой фильтр. При замене в выражении
. Это означает, что передаточная функция изображает полосовой фильтр. При замене в выражении 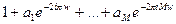
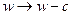 получим фильтр с комплексными коэффициентами. Формально - это решение задачи, однако использование комплексного фильтра для фильтрации вещественного сигнала не очень удобно. Поэтому используют выражение вида
получим фильтр с комплексными коэффициентами. Формально - это решение задачи, однако использование комплексного фильтра для фильтрации вещественного сигнала не очень удобно. Поэтому используют выражение вида 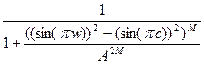 . Для четного
. Для четного 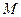 . Оно снова достигает максимума при
. Оно снова достигает максимума при 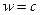 . Используя ту же технику, что и в предыдущем случае, после замены
. Используя ту же технику, что и в предыдущем случае, после замены 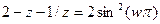 снова сведем задачу к отысканию корней квадратного уравнения.
снова сведем задачу к отысканию корней квадратного уравнения.
