Способы преобразования чертежа

СПОСОБ ПРОЕЦИРОВАНИЯ НА ДОПОЛНИТЕЛЬНУЮ ПЛОСКОСТЬ

Этот способ широко применяют в практике выполнения чертежей. Сущность способа проецирования на дополнительную плоскость проекций заключается в следующем: положение точек, линий, плоских фигур, геометрических тел в пространстве не изменяется, а данная система плоскостей проекций дополняется плоскостями, расположенными к П1 или П2, или друг к другу под прямым углом.

Каждая новая плоскость выбирается так, чтобы по отношению к заданным геометрическим элементам она заняла положение наиболее удобное для выполнения требуемого построения.

Рис. 6.4.

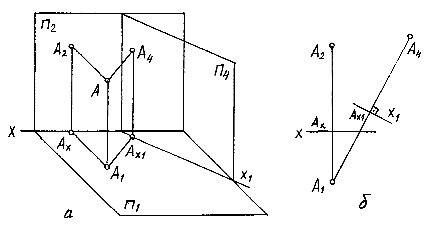
На рис.6.4 показано построение проекции точки А на дополнительную плоскость П4, перпендикулярную П1. П1 Ç П2 = х; П1 Ç П4 = х1. Перпендикуляры, опущенные из точки А на плоскостиП1, П2, П4, определят проекции А1, А2, А4. Из чертежа на рис.6.4а видно, что расстояние от дополнительной проекции А4 точки до оси х1 равно расстоянию от А2 до оси х, т.е. координате Z. Следовательно, можно сделать вывод, что расстояние от дополнительной проекции до новой оси равно той координате точки, которая отсутствует в плоскости, перпендикулярной к дополнительной.

Совместив далее П2 и П4 с плоскостью П1 вращением П2 вокруг оси х и П4 вокруг х1, получим комплексный чертеж точки А (рис.6.46). При наличии на чертеже двух основных проекций А1 иА2, дополнительную проекцию А4 построим следующим образом. Через А1 проведем линию связи, перпендикулярную х1. Отложив расстояние АX1А4, равное координате Z точки А, получим проекцию А4.

При введении дополнительной плоскости проекций, перпендикулярной П2, вдоль линии связи откладываем ту координату точки, которая отсутствует в плоскости П2, т.е. координату Y. ЕслиП4 ^ А3, то вдоль линии связи откладываем координату X.

Способом проецирования на дополнительную плоскость можно определить натуральную величину отрезка прямой. Для этого дополнительную плоскость располагают параллельно отрезку.

На рис.6.5 дополнительная плоскость П4 перпендикулярна П3. Новая ось х1 должна быть расположена относительно проекции прямой на плоскости, перпендикулярной к дополнительной, так же, как новая плоскость относительно прямой. В данном случае х1 ½½ А2В2. Вдоль линии связи от оси х1 откладываем ту координату точек А и В, которая отсутствует в плоскости П2 (плоскость, перпендикулярная к дополнительной),т.е. координату Y.

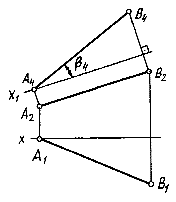Рис. 6.5.

Таким образом, прямая общего положения в системе плоскостей проекций П1 ^ П2 преобразована в прямую уровня в системе П4 ^ П2. Отрезок АВ на П4 спроецировался без искажения. Без искажения проецировался и угол наклона прямой к плоскости П2.

При решении некоторых задач приходится выполнять преобразование прямой уровня в проецирующую (рис.6.6). В этом случае дополнительная плоскость должна быть перпендикулярна прямой. Так как АВ ½½ П1, то П4 должна быть перпендикулярна П1. Тогда новая ось х1 ^ А1В1. Вдоль линии связи откладываем координату Z.

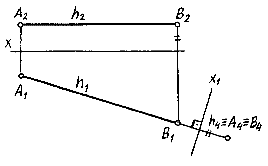Рис. 6.6.

Часто бывает необходимо плоскость общего положения преобразовать в проецирующую. Для того чтобы плоскость преобразовать в проецирующую следует любую прямую, принадлежащую плоскости, преобразовать в проецирующую. Для преобразования лучше выбрать прямую уровня, так как тогда уменьшается количество преобразований. На рис.6.7 преобразование треугольникаАВС в проецирующий выполнено с помощью горизонтали h, проведенной через точку А. Новая плоскость проекций П4 в этом случае должна быть перпендикулярна горизонтали h (ось х1перпендикулярна h1) и, соответственно, перпендикулярна плоскости проекций П1.

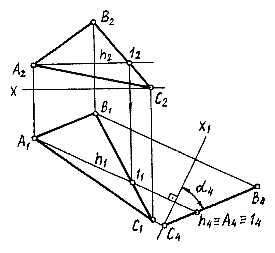Рис. 6.7. 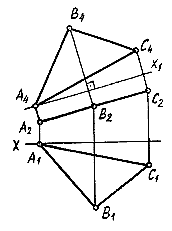Рис. 6.8.

После преобразования плоскости общего положения в проецирующую, можно найти натуральную величину плоской фигуры, преобразовав ее в плоскость уровня. На рис.6.8 плоскость S , заданная треугольником АВС, перпендикулярна фронтальной плоскости проекций. В этом случае новая плоскость П4, параллельная S , должна быть перпендикулярна П2. Ось х1 - параллельнаS1. Проекция А4В4С4 является натуральной величиной заданного треугольника.

Таким образом, последовательным введением двух дополнительных плоскостей проекций может быть определена натуральная величина плоской фигуры, принадлежащей плоскости общего положения.

СПОСОБ ВРАЩЕНИЯ

Способ вращения геометрической фигуры вокруг некоторой оси состоит в том, что фигура вращается вокруг оси до требуемого положения относительно заданной неподвижной системы плоскостей проекций.

В качестве оси вращения может быть взята любая прямая. В практике же преобразования комплексного чертежа широкое распространение получило вращение вокруг проецирующих прямых и линий уровня.

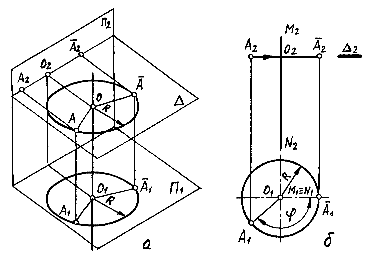Рис. 6.1.

При вращении некоторой точки вокруг оси она описывает окружность, расположенную в плоскости, перпендикулярной оси вращения. На рис.6.1 рассмотрено вращение точки А вокруг горизонтально проецирующей оси. Плоскость вращения D параллельна плоскости П1 и на фронтальной проекции изображается следом D2. Горизонтальная проекция О1 центра вращения Осовпадает с проекцией M1N1 оси, а горизонтальная проекция О1А1 радиуса вращения является его натуральной величиной. Вращаясь вокруг оси, точка А перемещается по окружности, которая на А1 проецируется в окружность, а на П2 - в отрезок прямой, параллельный оси х. На рис.6.1 поворот произведен на угол j против часовой стрелки так, чтобы в новом положении точки радиус вращения был параллелен плоскости П2.

Если точку вращать вокруг оси, перпендикулярной плоскости П2, то ее фронтальная проекция будет перемещаться по окружности, а горизонтальная - параллельно оси х.

Вращение вокруг проецирующей прямой применяют при решении задачи на определение натуральной величины отрезка прямой (рис.6.2). Ось вращения выбирают так, чтобы она проходила через одну из крайних точек отрезка, например, через точку В. Тогда при повороте точки А на угол j в положение А отрезок АВ перемещается в положение АВ, параллельное плоскости П2. В этом случае отрезок будет проецироваться на П2 в натуральную величину ( ½В 2А2 ½= ½ВА ½). Одновременно в натуральную величину будет проецироваться угол а наклона отрезка АВ к плоскости П1.

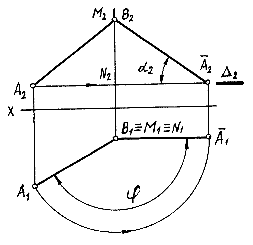Рис. 6.2.

Натуральную величину плоской фигуры удобнее находить с помощью вращения вокруг прямой уровня. Путем такого вращения плоскость, которой принадлежит рассматриваемая фигура, поворачивают в положение, параллельное плоскости проекций. При таком положении плоскости любая принадлежащая ей фигура будет проецироваться в натуральную величину.

Вращая плоскость вокруг горизонтали, можно перевести ее в положение, параллельное плоскости П1. Вращение плоскости вокруг фронтали позволяет перевестиее в положение, параллельное плоскости П2.

На рис.6.3 рассмотрено нахождение натуральной величины треугольника АВС при помощи вращения его вокруг горизонтали. Каждая точка плоскости треугольника АВС при вращении перемещается по окружности, перпендикулярной оси вращения. Так, точка В перемещается по окружности, плоскость D которой перпендикулярна горизонтали. Центр окружности О находится на оси вращения, а величина радиуса равна расстоянию от точки до оси вращения. Так как точка В вращается вокруг горизонтали, то окружность проецируется на П1 в отрезок прямой, перпендикулярный горизонтали, а на П2 - в эллипс, который можно не строить.

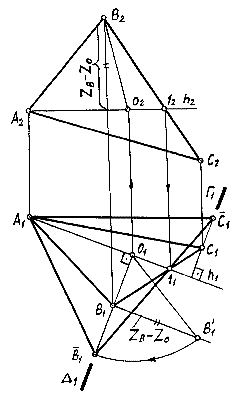Рис. 6.3.

На рис.6.3 видно, что и на П1, и на П2 радиус вращения проецируется с искажением. Натуральную величину радиуса находим методом прямоугольного треугольника (см. свойство ортогонального проецирования). Для этого принимаем горизонтальную проекцию О1В1 за катет прямоугольного треугольника. Второй катет должен быть равен разности координат Z концов отрезка OB (ZВ - Z0). Гипотенуза треугольника О1В1В1' (О1В1') равна R. После поворота плоскость треугольника будет параллельна П1. Следовательно, 0В спроецируется на П1 в натуральную величину. Горизонтальную проекцию нового, после поворота, положения точки В (В1') находим на пересечении дуги окружности, проведенной из горизонтальной проекции центра вращенияО1, радиусом, равным О1В1, с горизонтальной проекцией плоскости A (А1).

Точка С также перемещается по окружности, плоскость которой Г перпендикулярна горизонтали. Точка 1 находится на горизонтали, поэтому при вращении не перемещается. Так как точки В, 1и С находятся на одной прямой, то горизонтальную проекцию нового, после поворота, положения точки С найдем на пересечении прямой, проведенной через В1 и 11, с горизонтальной проекцией плоскости Г (Г1).