Комплексные числа и действия над ними
ГЛАВА 1. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИИ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
Комплексным числом 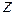 называется выражение вида
называется выражение вида
 , (1.1)
, (1.1)
где 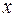 и
и  действительные числа, а
действительные числа, а  мнимая единица, определяемая равенством
мнимая единица, определяемая равенством  или
или  . Числа
. Числа 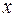 и
и 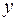 называются действительной и мнимой частями комплексного числа z и обозначаются
называются действительной и мнимой частями комплексного числа z и обозначаются  ,
,  .
.
Форму (1.1) комплексного числа 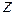 называют алгебраической. Два комплексных числа
называют алгебраической. Два комплексных числа  и
и  считаются равными, если равны их действительные и мнимые части:
считаются равными, если равны их действительные и мнимые части:  ,
,  . Число
. Число 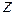 равно 0 при условии
равно 0 при условии  .
.
Понятия «больше» и «меньше» для комплексных чисел не устанавливаются.
Число  называется сопряженным числу
называется сопряженным числу 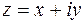 .
.
Алгебраические действия над комплексными числами определяются следующими равенствами:
 ,
,

 ,
,

Комплексное число 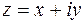 изображается точкой
изображается точкой  на координатной плоскости
на координатной плоскости 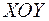 (рис.1.1). При этом действительные числа
(рис.1.1). При этом действительные числа 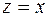 изображаются точками на оси
изображаются точками на оси 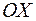 , называемой здесь действительной осью, а мнимые числа
, называемой здесь действительной осью, а мнимые числа  изображаются точками оси
изображаются точками оси 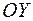 , называемой мнимой осью. Плоскость, на которой изображают комплексные числа, называется комплексной плоскостью.
, называемой мнимой осью. Плоскость, на которой изображают комплексные числа, называется комплексной плоскостью.
 Рис.1.1 Рис.1.1 | Комплексное число 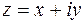 может быть изображено вектором может быть изображено вектором  с координатами x и y и с началом в точке с координатами x и y и с началом в точке  (рис.1.1). Длина (рис.1.1). Длина  вектора вектора  , изображающего комплексное число z, называется модулем комплексного числа. Угол , изображающего комплексное число z, называется модулем комплексного числа. Угол  , образуемый этим вектором с положительным направлением действительной оси, называется аргументом комплексного числа. , образуемый этим вектором с положительным направлением действительной оси, называется аргументом комплексного числа. |
Модуль числа принято обозначать  , а аргумент
, а аргумент  .
.
Для модуля и аргумента, как видно на рис.1.1, справедливы формулы
 , (1.2)
, (1.2)
 (при
(при  ). (1.3)
). (1.3)
Величина  имеет бесконечное множество значений, определяемых с точностью до целого кратного числа
имеет бесконечное множество значений, определяемых с точностью до целого кратного числа  . Если величину одного из углов обозначить через
. Если величину одного из углов обозначить через  , то совокупность величин всех углов запишется в виде:
, то совокупность величин всех углов запишется в виде:


Значение  , принадлежащее промежутку
, принадлежащее промежутку  , называется главным и обозначается
, называется главным и обозначается  . Итак,
. Итак,
 , (1.4)
, (1.4)

 (1.5)
(1.5)
В силу формулы (1.3) и определения (1.4) находим, что

Если действительная часть  , то
, то  при
при  , и
, и  , при
, при  .
.
Комплексному числу 0не приписывается какое-либо значение аргумента.
Зная модуль комплексного числа  и его аргумента
и его аргумента  , мы можем вычислить его действительную часть x и мнимую y:
, мы можем вычислить его действительную часть x и мнимую y:
 и записать число z в форме
и записать число z в форме
 (1.6)
(1.6)
Эту форму комплексного числа называют тригонометрической.
Имеют место следующие правила умножения, деления, возведения в целую положительную степень и извлечение корня для чисел z в тригонометрической форме:
 , (1.7)
, (1.7)
 , (1.8)
, (1.8)
 ,
,  , (1.9)
, (1.9)
 , (1.10)
, (1.10)
где  .
.
Формула (1.9) при  называется формулой Муавра.
называется формулой Муавра.
Геометрически n значений выражения  (1.10) изображаются вершинами некоторого правильного n – угольника, вписанного в окружность, с центром в начале координат и с радиусом
(1.10) изображаются вершинами некоторого правильного n – угольника, вписанного в окружность, с центром в начале координат и с радиусом  .
.
Условимся выражение  обозначать символом
обозначать символом  , т.е.
, т.е.
 , (1.11)
, (1.11)
не придавая этой записи пока никакого другого смысла, кроме как обозначения. Далее будет показано, что символ  обладает свойствами показательной функции, для которой справедлива формула (1.11), называемая формулой Эйлера.
обладает свойствами показательной функции, для которой справедлива формула (1.11), называемая формулой Эйлера.
Используя обозначение (1.11), умножив левую и правую части на r, можно перейти от тригонометрической формы (1.6) к показательной форме комплексного числа
 (1.12)
(1.12)
Ввиду ее компактности она удобнее равносильной тригонометрической формы.
Алгебраические действия (1.7) – (1.10) над комплексными числами в показательной форме (1.12) имеют более рациональный вид:
 , (1.13)
, (1.13)
 , (1.14)
, (1.14)
 , (1.15)
, (1.15)
 ,
,  (1.16)
(1.16)
При решении задач полезно помнить, что  ,
,  ,
,  ,
,  и т.д., и вообще при любом целом
и т.д., и вообще при любом целом 
 ,
,  ,
,  ,
,  .
.
УПРАЖНЕНИЯ
1. Решить уравнение  .
.
Решение. 1-й способ:  .
.
 ,
,  ,
,  .
.
2-й способ: В результате подстановки 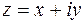 в данное уравнение имеем
в данное уравнение имеем  , откуда после преобразований получим систему уравнений
, откуда после преобразований получим систему уравнений  . Решая систему, получим
. Решая систему, получим  ,
,  .
.
2. Найти  и
и  , если
, если  .
.
Решение:  , откуда
, откуда  ,
,  .
.
3. Выяснить геометрический смысл модуля разности  двух комплексных чисел
двух комплексных чисел  и
и  .
.
Решение:  .
.
Следовательно,  есть расстояние между точками
есть расстояние между точками  , и
, и  (рис. 1.2).
(рис. 1.2).
 Рис.1.2 Рис.1.2 | Если изобразить комплексное число с помощью вектора, то действительная и мнимая части вектора  являются координатами вектора, а так как при вычитании векторов их координаты соответственно вычитаются, то вычитание комплексных чисел являются координатами вектора, а так как при вычитании векторов их координаты соответственно вычитаются, то вычитание комплексных чисел |
сводится к вычитанию векторов, изображающих эти числа.
Как видно из рис. 1.2,  есть длина вектора
есть длина вектора  , т.е. расстояние между точками, изображающими числа
, т.е. расстояние между точками, изображающими числа  и
и  .
.
4. Найти модуль и главное значение аргумента комплексного числа  , представить его в тригонометрической и показательной формах.
, представить его в тригонометрической и показательной формах.
Решение. По определению модуля  . Так как значения аргумента
. Так как значения аргумента  удовлетворяют соотношению
удовлетворяют соотношению  , то
, то  . Итак,
. Итак,  ,
,  и согласно (1.6) и (1.12) имеем
и согласно (1.6) и (1.12) имеем  ,
,  .
.
5. Для комплексных чисел  и
и  , вычислить
, вычислить  и
и  , представив их вначале в тригонометрической форме.
, представив их вначале в тригонометрической форме.
Решение.  ,
,  . Применяя формулы (1.7) и (1.8), получим
. Применяя формулы (1.7) и (1.8), получим


6. Вычислить  .
.
Решение. Запишем число  в тригонометрической форме. По формуле (1.9) имеем
в тригонометрической форме. По формуле (1.9) имеем 

 .
.
7. Вычислить и изобразить на комплексной плоскости все значения  .
.
Решение. Представим  в тригонометрической форме (1.6), для чего найдем модуль и главное значение аргумента
в тригонометрической форме (1.6), для чего найдем модуль и главное значение аргумента  ,
,  . Имеем
. Имеем  .
.
Применяя формулу (1.10), найдем 3 значения корня, содержащихся в формуле  , где
, где  . Воспользовавшись показательной и тригонометрической формами числа (1.6), (1.12), получаем
. Воспользовавшись показательной и тригонометрической формами числа (1.6), (1.12), получаем
при 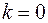
 ,
,
при 
 ,
,
при 
 .
.
Точки 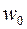 ,
,  ,
,  образуют вершины правильного треугольника, вписанного в окружность радиуса 2 с центром в начале координат (рис. 1.3).
образуют вершины правильного треугольника, вписанного в окружность радиуса 2 с центром в начале координат (рис. 1.3).
8. Решить уравнение  .
.
Решение. Нахождение всех корней уравнения сводится к задаче: найти все значения корня  . Для чего запишем число
. Для чего запишем число  в показательной форме
в показательной форме  и применим формулу (1.16)
и применим формулу (1.16)  , где
, где 
 .
.
При 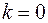
 , откуда следует, что
, откуда следует, что  ,
,  .
.
При 
 , откуда следует, что
, откуда следует, что  ,
,  .
.
При 
 ,
, 
 ,
,  .
.
При 
 ,
, 
 ,
,  .
.
 Рис.1.3 Рис.1.3 |  Рис.1.4 Рис.1.4 |
Как видно из рис. 1.4, точки  ,
,  ,
,  ,
,  комплексной плоскости лежат в вершинах квадрата (на окружности радиуса
комплексной плоскости лежат в вершинах квадрата (на окружности радиуса  с центром в начале координат).
с центром в начале координат).
