Развертка гранных поверхностей
Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью всех его граней. Развертывание гранных поверхностей выполняют для проведения раскроя листового материала при изготовлении деталей или определения площади поверхности деталей, покрываемых различными материалами. Определение площади важно при различных покрытиях, выполняемых как с декоративными целями, так и с целью придания поверхности определенных свойств, например повышенной электропроводности, а также при различных химических методах обработки поверхностей.
Для построения развертки гранной поверхности необходимо определить размеры ее граней. Заметим, что построение любой грани многогранника может быть выполнено путем разбивки ее на треугольники. Длина сторон треугольника в свою очередь может быть определена любым из известных методов.
Развертка поверхности пирамиды. Построение развертки боковой поверхности пирамиды можно проводить в следующей последовательности:
определить длину ребер и сторон основания пирамиды; выполнить чертеж развертки последовательным построением треугольников — граней пирамиды.
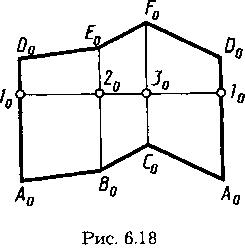
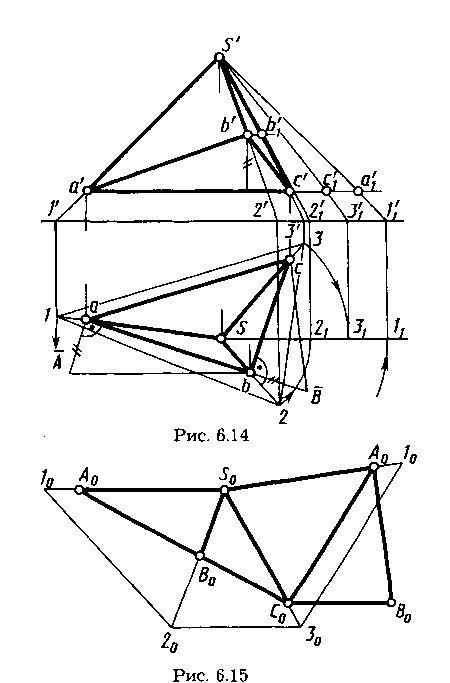
Пример построения развертки поверхности треугольной пирамиды SABC приведен на рисунках 6.14 и 6.15. Для удобства построения на рисунке 6.14 боковые ребра пирамиды продолжены до пересечения с плоскостью Н. Это позволило определить на горизонтальной проекции длину отрезков 1—2, 2—3, 3—4 нового основания пирамиды. Длина боковых ребер S—l, S—2, S—3найдена вращением их вокруг вертикальной оси — отрезки s'11', s'21', s'31'. На них найдены отрезки s'a1', s'b1', s'c1'. По найденным отрезкам на рисунке 6.15 построена развертка боковой поверхности Solo2o3o1o и затем S0A0BoCoAo. На отрезке А0С0 построена натуральная величина треугольника А0В0С0 по сторонам A0В0 и C0B0, найденным способом прямоугольного треугольника (см. рис. 2.9).
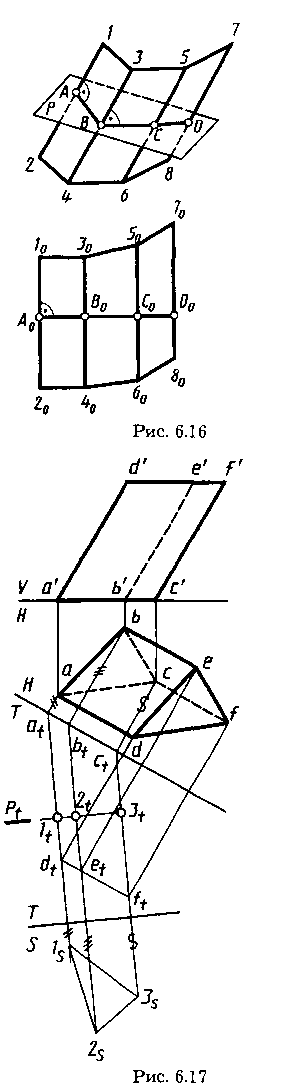
Построение развертки призматической поверхности можно производить несколькими способами — нормального сечения, треугольников.
При способе нормального сечения построение развертки призматической поверхности целесообразно выполнять в следующем порядке (рис. 6.16):
пересечь призматическую поверхность вспомогательной плоскостью, перпендикулярной к ее ребрам (Р перпендикулярно 1—2; нормальное сечение);
развернуть построенную ломаную линию (А0В0С0D0) пересечения вспомогательной плоскости с призматической поверхностью, определив длину ее отрезков (А0B0, В0С0,, C0D0);
на перпендикулярах к развернутой линии пересечения (А0D0) отложить длину отрезков ребер призматической поверхности (А020,ВоЗо, Bo4o, Сo5о, Со6о, Do7o, Do8o) и соединить их концы отрезками прямых.
Пример построения развертки боковой поверхности наклонной призмы на чертеже приведен на рисунке 6.17 и 6.18. Для построения вспомогательной плоскости Р, перпендикулярной ребрам призмы, выбрана дополнительная плоскость проекций Т, параллельная ребрам призмы и перпендикулярная плоскости Н. Вспомогательная плоскость Р задана следом Pt на плоскости проекций Т перпендикулярно ребрам призмы. Проекции на плоскости Т точек пересечения ребер призмы с плос-
костью Р отмечены 1t, 2t, 3t. На плоскость Т боковые ребра призмы проецируются в натуральную величину. Натуральная величина отрезков линии пересечения 1—2—3 плоскостью Р,перпендикулярной ребрам, определена на плоскости S (пл. S перпендикулярно T).
По способу треугольников развертка призматической поверхности заключается в следующем: четырехугольники (грани) разбивают диагоналями на треугольники; определяют длины сторон треугольников; выполняют чертеж развертки последовательным построением треугольников, на которые разбиты грани.