Кинематический анализ механизма методом диаграмм

КУРСОВОЙ ПРОЕКТ

ПО ТЕОРИИ МЕХАНИЗМОВ И МАШИН

Тема:

Задание:

Вариант: 5D9

Выполнил:студент группы

Проверил:профессор

Поезжаева Е.В.

Пермь 2013г.

Содержание:

1. Структурный анализ механизма………………………………………………3

2. Кинематический анализ механизма…………………………………………..4

3. Кинетостатический анализ механизма…………………………………….…9

4. Расчёт маховика………………………………………………………............12

5. Профилирование кулачка……………………………………………………17

6. Проектирование зубчатой передачи………………………………………...20

7. Указания по выполнению расчётов для курсового проекта по ТММ…….23

8. Список литературы…………………………………………………………...24

СТРУКТУРНЫЙ AНАЛИ3 КРИВОШИПНО-ПОЛЗУННОГО МЕХАНИЗМА

1. Изобразим структурную схему механизма

ОА — кривошип - совершает вращательное движение;

АВ - шатун - совершает плоскопараллельное движение;

В - ползун - совершает поступательное движение.

2. Найдем степень подвижности механизма по формуле Чебышева:

W=3n-2p5-p4

3. Разложим на структурные группы Ассура

4. Запишем структурную формулу механизма I=>II²₂

5. Определим класс, порядок всего механизма.

Исследуемый механизм состоит из механизма первого класса и структурной группы второго класса второго порядка (шатун и ползун), следовательно, гидронасос ОАВ - механизм второго класса второго порядка.

КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА

Исходные данные: OA⁼ м, AB⁼ мм

w1 = с^-1

При кинематическом анализе решаются три задачи:

задача о положениях;

задача о скоростях;

задача об ускорениях.

ЗАДАЧА О ПОЛОЖЕНИЯХ

Проектирование кривошипно-ползунного механизма, Найдем крайние положения механизма: начало и конец рабочего хода. Начало рабочего хода найдем по формуле:

S'=l+r

где

l -длина кривошипа ОА

г - длина шатуна АВ

Конец рабочего хода найдем по формуле:

S"=l-r[м];

Рабочий ход

S=S' - S"=2r [м];

Построим механизм в масштабе

m1 = AB / OA= [м / мм]

Найдем длину АВ:

АВ = AB/m1= [мм]

Покажем перемещение точек в двенадцати положениях механизма. Для этого разделим ок­ружность на 12 равных частей (используя метод засечек).

Построим шатунную кривую. Для этого найдем центр тяжести каждого звена и соединим плавной линией.

Планы положений механизма используются для определения скоростей и ускорений в за­данных положениях.

ЗАДАЧА О СКОРОСТЯХ

Кинематический анализ выполняется графоаналитическим методом, который отражает на­глядность изменения скоростей и обеспечивает достаточную точность. Скорость ведущего звена:

[мс^-1]

Запишем векторные уравнения:

V_B = V_A+V_AB ; V_B = V_X+V_BX

где V_X=0; V_A ^OA; V_AB ^ AB; V_BX ½½ BX

Величины векторов V_BA, V_B, V_S2 определим построением. Выберем масштаб плана скоростей

[мс^-1/мм].

Ге pa - отрезок, характеризующий величину скорости на чертеже = мм. От произвольной точки р - полюса плана скоростей отложим вектор ра,

перпендикулярный ОA. Через т. а проводим перпендикулярно АВ прямую. Точка пересечения оси х (выбранной в направлений т. в) с этой прямой даст т. в, соединив т. в с полюсом получим вектор скорости т. в. Оп­ределим величину скорости т. в:

[мс^-1]

Положение т. на плане скоростей определим из пропорции:

Соединив т. S₂ с полюсом р, получим величину и направление скорости т. S2:

[мс^-1]

[мс^-1]

Определим:

[мс^-1]

[мс^-1]

[мс^-1]

Определим:

[с^-1]

Направление w2 определяется переносом вектора vba в т.В относительно т.А.

Параметр

Положение механизма

VBA мс-1

Vnx МС-1

Vsi мс-1

VS2 мс-1

Vs3 мс-1

w2 с-1

ГОДОГРАФ СКОРОСТЕЙ

Полученные вектора скорости t.S₂; в двенадцати положениях механизма приведем к одной точке и соединим их вершины плавной линией.

ЗАДАЧА ОБ УСКОРЕНИЯХ

Начнем исследование механизма с первого класса, определяем ускорение точки А:

[мс^-2]

Переходим к исследованию группы П². Запишем векторные уравнения:

где аА - ускорение центра шарнира, аА параллельно ОА; аⁿВА- нормальное ускорение центра шарнира А при вращении звена (параллельно ОА)

[мс^-2/_мм]

а^t_ВА - касательное ускорение той же точки в том же движении (перпендикулярно AD). Выберем масштаб плана ускорений:

= [мс^-2/_мм].

Где pа - отрезок, характеризующий величину ускорения на чертеже =мм.Вычислим длину отрезка an, в котором должен отображаться на плане ускорений вектор ускоре­ния аⁿ_ВА.

[мм]

Построим план ускорений. Из произвольной точки p - полюса откладываем отрезки pa и an. Из точки п проводим прямую, перпендикулярную an.

Пересечение оси Х с этой прямой даст т. в.

Соединив т. в с т. а получим аВА. Положение т. S2 на плане ускорений найдем аналогично. Соединив т. S2 с полюсом p получим, пользуясь планом ускорений, величину и направление вектора аS2=p*S2*m2

Определим величины ускорений:

[мс^-2]

[мс^-2]

[мс^-2]

[мс^-2]

[мс^-2]

Определим 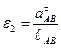, направление определяется переносом вектора в т.В относительно т.А.

Параметр	Положение механизма
vba, мс-1
ава, мс-2
ава, мс-2
an, мм
ава, мс-2
ав, мс-2
аs1, мс-2
аs2, мс-2
аs3, мс-2
e2, c-2

КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА МЕТОДОМ ДИАГРАММ

ЗАДАЧА О ПОЛОЖЕНИЯХ S = f(j)

Выбираем масштаб построения mS= = м/мм. Проводим оси прямоугольных координат S и j. На оси откладываем 12 равных отрезков 0-1, 1-2, 2-3 и т.д. в соответствие углу поворота кривошипа (180°). Через точки 1, 2, 3 и т.д. проводим ординаты и откладываем на них отрезки, равные перемещению т. В при соответствующих положениях кривошипа. Соединив точки, получим диаграмму перемещения т. В, т.е. Sb = f(j);

[^рад/_мм]

ЗАДАЧА О СКОРОСТЯХ V_u = f(j)

Решение задачи методом хорд . Для этого разобьем кривую перемещений Sb = f(j), на ряд участков 0-1, 1-2, 2-3 и т.д. На каждом из этих участков, заменив кривую хордой.

На оси j диаграммы Vb = f(j), отложим отрезок Н= мм, величину выбираем произвольно. Из т. O1 проводим лучи O1-l, O1-2 и т.д. параллельно хордам 0-1, 1-2, 2-3 и т.д. График средней скорости получают, проводя плавную кривую через середины положений.

[мс^-1/мм]