Применение вспомогательных секущих плоскостей
Рассмотрим применение вспомогательных секущих плоскостей на примере построения линии пересечения сферы с конусом вращения (рис. 10.2).
Для построения линии пересечения заданных поверхностей удобно в качестве вспомогательных поверхностей использовать серию горизонтальных плоскостей, перпендикулярных оси конуса, которые пересекают сферу и конус по окружностям. На пересечении этих окружностей находят точки искомой линии пересечения.
Построение начинают обычно с отыскания проекций характерных точек. Проекции 1 'высшей и 2' низшей точек являются точками пересечения фронтальных проекций очерков, так
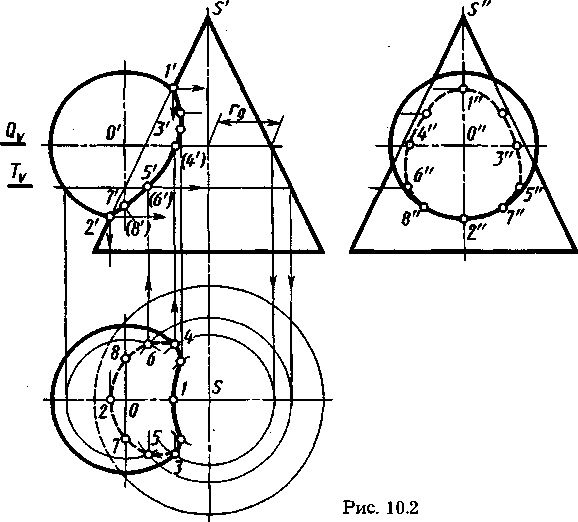
как центр сферы и ось конуса лежат в плоскости, параллельной плоскости V. Их горизонтальные 1, 2 и профильные 1'\ 2" проекции находят в проекционной связи. Проекции 3', 3, 3" и 4\ 4, 4",лежащие на экваторе сферы, находят с помощью горизонтальной плоскости Q (Qv), проходящей через центр сферы О (о'). Она пересекает сферу по экватору и конус по окружности радиуса rq, в пересечении горизонтальных проекций которых и находят горизонтальные проекции 3, 4 точек искомой линии пересечения. Горизонтальные проекции 3 и 4 этих точек являются границами видимости участков линии пересечения на этой проекции. Проекции промежуточных точек, например 5' 5, 5" и 6\ 6, 6", находят с помощью вспомогательной горизонтальной плоскости Т(Tv).Их построение ясно из чертежа. Аналогично построены другие точки. Профильные проекции точек линии пересечения строят по их фронтальной и горизонтальной проекциям. Точки с проекциями 7' 7, 7" и 8\ 8, 8" являются границами видимости участков профильной проекции линии пересечения. Ниже проекций 7" и 8" профильная проекция линии пересечения видима.
построение линии пересечения поверхностей вращения способом концентрических сфер
Этот способ применяется для построения линии пересечения двух поверхностей вращения, оси которых пересекаются. Для упрощения графического решения необходимо, чтобы плоскость, определяемая осями поверхностей вращения» была параллельной какой-либо плоскости
проекций. В противном случае эта плоскость должна быть предварительно переведена в удобное для решения задачи положение одним из способов преобразования чертежа. 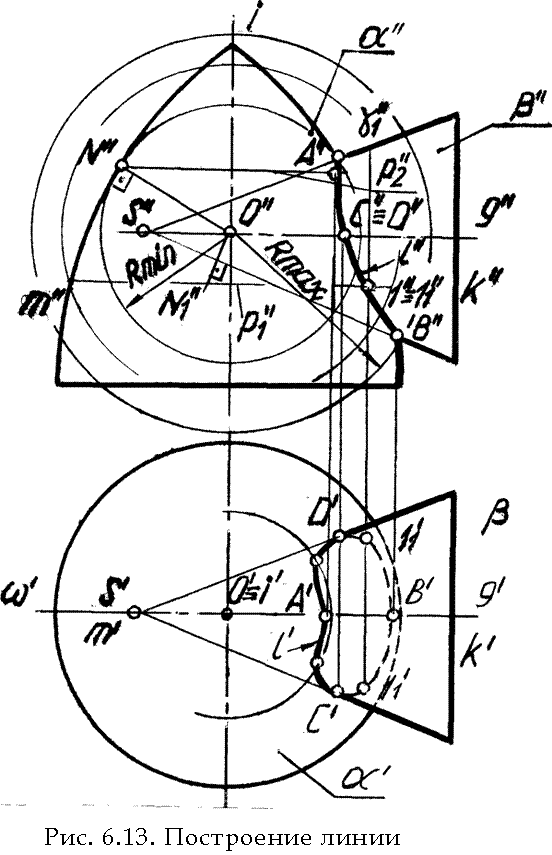
В основу способа концентрических сфер положены теорема о пересечении двух соосных поверхностей вращения и следствие из неё.
Пример 8. Построить линию пересечения L произвольной поверхности вращения ос(1}т) и конической поверхности вращения fi(S;K), имеющих общую плоскость симметрии сд (со ') .
Решение . Прежде всего построим экстремальные точки линии переселения А (А") к В (В") -точки пересечения главных меридианов обеих пересекающихся поверхностей /рис. б. 13/. За центр вспомогательных сфер ft примем точку 0(0")*L'(Cj". Для определения пределов изменения радиусов вспомогательных сфер выбираем отрезок 0"В'[ равный расстоянию от центра О (Ои)&о наиболее удаленной экстремальной точки В (&") » который будет ра диуеом максимальной сферы. Радиус минимальной сферы равен радиусу большей из двух сфер, вписанных в данные по верхности, то есть отрезку О"N" . Проведя достаточное количество сфер поверхностей вращенияполучим множество точек, определяющих с достаточной, степенью точности линию пересечения поверхностей L
На рис» 6.13 показаны все построения для одной сферы-посредника . Эта сфера соосна с поверхностями конуса..
16. Построение точки пересечения прямой общего положения с проецирующей плоскостью
Рис. 7.4.
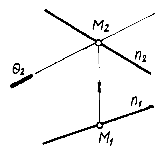
 В качестве примера построим точку встречи фронтально проецирующей плоскости с прямой общего положения n (рис.7.4). Пусть n = = М. М2 - фронтальная проекция искомой точки Мдолжна лежать на фронтальной проекции П2 прямой n, как точка, принадлежащая прямой n. В то же время фронтальная проекция М2 точки М должна лежать на следе 2 плоскости , так как искомая точка принадлежит и плоскости . Следовательно, искомая фронтальная проекция М2 точки М может лежать только на пересечении n2 и 2. Имея фронтальную проекцию М2 точкиМ, при помощи линии связи легко найти ее горизонтальную проекцию.
В качестве примера построим точку встречи фронтально проецирующей плоскости с прямой общего положения n (рис.7.4). Пусть n = = М. М2 - фронтальная проекция искомой точки Мдолжна лежать на фронтальной проекции П2 прямой n, как точка, принадлежащая прямой n. В то же время фронтальная проекция М2 точки М должна лежать на следе 2 плоскости , так как искомая точка принадлежит и плоскости . Следовательно, искомая фронтальная проекция М2 точки М может лежать только на пересечении n2 и 2. Имея фронтальную проекцию М2 точкиМ, при помощи линии связи легко найти ее горизонтальную проекцию.
7.2.2.Построение точки пересечения плоскости общего положения с проецирующей прямой
Рис. 7.5.
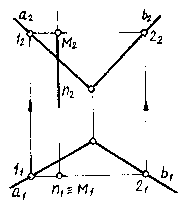
На рис.7.5 показано построение точки встречи горизонтально проецирующей прямой n с плоскостью общего положения (a b). Горизонтальные проекции всех точек, принадлежащих данной прямой, в том числе и горизонтальная проекция М1 искомой точки М, будут совпадать с n1 - горизонтальной проекцией прямой n. Следовательно, задача сводится к нахождению недостающей фронтальной проекции М1 точки М, лежащей в плоскости . Через М1 проведем прямую 1121. По линиям связи найдем фронтальные проекции 12, 22 точек 1 и 2, через которые проведем фронтальную проекцию прямой 12. На пересечении 1222 с n2 и будет находиться фронтальная проекция М2 точки М.
