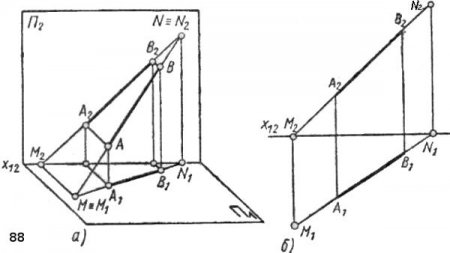
Прямые общего положения. Следы прямой
Построение чертежа по методу Монжа. Четверти и октанты пространства
Монж впервые дал научное обоснование общего метода построения изображений, предложив рассматривать плоский чертёж, состоящий из двух проекций, как результат совмещения двух взаимно перпендикулярных плоскостей проекций. Для получения изображений предметов на чертежах Монж предложил использовать метод параллельного прямоугольного проецирования на взаимно перпендикулярные плоскости проекций (фронтальная плоскость проекций V, горизонтальная плоскость проекций H, профильная плоскость проекций W).Плоскости проекций, пересекаясь в пространстве, делят его на восемь частей, которые называются октантами. Три взаимно перпендикулярные плоскости проекций делят пространство на восемь подпространств – октантов. Для получения изображения предмет располагают в 1-ой октанте между наблюдателями и плоскостями проекций. Плоскости проекций пересекаются между собой по линиям, которые называются осями проекций. Эти оси пересекаются в точке О- точке начала координат. Оси проекций принимают за оси координат – натуральной системой прямоугольных координат. Две взаимно перпендикулярные плоскости проекций делят пространство на четыре подпространства - четверти.
Центральное и параллельное проецирование. Их виды
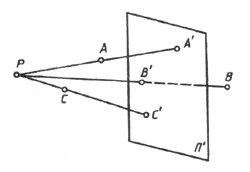
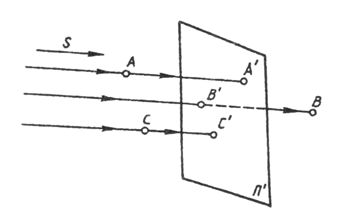
Проекция –это изображение объекта на плоскости. Плоскость проекций – плоскость, на которой строится изображение. Проецирующий луч – прямая линия соединяющая объект проецирования и проекцию. Проекцией точки называется точка пересечения проецирующего луча с плоскостью проекции. Проекции называются параллельными, если проецирующие лучи параллельны между собой, и центральными, если все проецирующие лучи проходят через одну точку – центр проекций S. Свойства проекций при центральном проецировании:Проекцией точки является точка. Проекцией линии является линия. Проекцией прямой в общем случае является прямая. (Если прямая совпадает с проецирующим лучом, то её проекцией является точка). Если точка принадлежит линии, то проекция точки принадлежит проекции линии. Точка пересечения линий проецируется в точку пересечения проекций этих линий. В общем случае плоский многогранник проецируется в многогранник с тем же числом вершин. Проекцией взаимно параллельных прямых является пучок прямых. Если плоская фигура параллельна плоскости проекций, то её проекция подобна этой фигуре.Параллельные проекции могут быть:прямоугольными - если проецирующие лучи перпендикулярны плоскости проекций; косоугольными – если проецирующие лучи не перпендикулярны плоскости проекций; Свойства параллельного проецирования:проекция точки является точка; проекцией прямой линии в общем случае является прямая; если точка делит отрезок прямой в определенном отношении, то проекция точки делит отрезок прямой в том же отношении; если прямые в пространстве параллельны, то их одноименные проекции на чертеже также параллельны; проекции параллельных прямых параллельны; плоская фигура, параллельная плоскости проекций, проецируется без искажения.
Прямые общего положения. Следы прямой
Прямые общего положения не параллельны, а соответственно, и не перпендикулярны плоскостям проекций H, V и W. Поэтому на чертеже их проекции не параллельны и не перпендикулярны осям проекций Х, У и Z и искажают натуральную величину этих прямых.
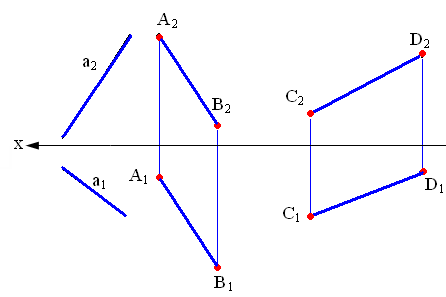Теорема о принадлежности точки прямой: если точка принадлежит прямой, то на чертеже проекции точки лежат на одноименных проекциях прямой. Следы прямой называются точки ее пересечения с плоскостями проекций. 